Δύναμη μεταξύ μαγνητών
| Αυτό το λήμμα χρειάζεται επιμέλεια ώστε να ανταποκρίνεται σε υψηλότερες προδιαγραφές ορθογραφικής και συντακτικής ποιότητας ή μορφοποίησης. Αίτιο: επιμέλεια μετάφρασης, ακατανόητο κείμενο Για περαιτέρω βοήθεια, δείτε τα λήμματα πώς να επεξεργαστείτε μια σελίδα και τον οδηγό μορφοποίησης λημμάτων. |
Οι μαγνήτες ασκούν δυνάμεις και ροπές ο ένας στον άλλο λόγω των κανόνων του ηλεκτρομαγνητισμού. Οι δυνάμεις του πεδίου έλξης των μαγνητών οφείλονται σε μικροσκοπικά ρεύματα ηλεκτρικά φορτισμένων ηλεκτρόνιων τροχιάς και τον εγγενές μαγνητισμό των θεμελιωδών σωματιδίων (όπως τα ηλεκτρόνια) που αποτελούν το υλικό. Και τα δύο αυτά διαμορφώνονται αρκετά καλά όσο οι μικροσκοπικοί βρόχοι του ρεύματος που ονομάζονται μαγνητικά διπόλα που παράγουν το δικό τους μαγνητικό πεδίο και επηρεάζονται από εξωτερικά μαγνητικά πεδία. Η πιο στοιχειώδης δύναμη μεταξύ μαγνητών είναι η μαγνητική αλληλεπίδραση διπόλου-διπόλου. Εάν όλα τα μαγνητικά διπόλα που αποτελούν δύο μαγνήτες είναι γνωστά, τότε η καθαρή δύναμη και στους δύο μαγνήτες μπορεί να προσδιοριστεί με τη σύναψη όλων αυτών των αλληλεπιδράσεων μεταξύ των διπόλων του πρώτου μαγνήτη και του δεύτερου.
Είναι συχνά πιο βολικό να μοντελοποιήσετε τη δύναμη μεταξύ δύο μαγνητών που οφείλεται σε δυνάμεις μεταξύ μαγνητικών πόλων που έχουν μαγνητικές ιδιότητες που έχουν εξαπλωθεί πάνω τους. Η θετική (βόρειος πόλος) και αρνητική (νότιος πόλος) ή και αντίστροφα ,μαγνητική φόρτιση συνδέεται πάντοτε με μια σειρά μαγνητισμένου υλικού. Δεν έχουμε παρατηρήσει ποτέ μαγνητικά μονόπολα , αν και έχουν προταθεί από επιφανείς επιστήμονες όπως ο Ντίρακ εξηγώντας έτσι την κβάντωση του ηλεκτρικού φορτίου.Αυτό το μοντέλο λειτουργεί καλά στην πρόβλεψη των δυνάμεων μεταξύ απλών μαγνητών όπου είναι διαθέσιμα καλά μοντέλα του τρόπου διανομής της μαγνητικής χρέωσης.
Μαγνητικοί πόλοι έναντι ατομικών ρευμάτων[Επεξεργασία | επεξεργασία κώδικα]

Το πεδίο ενός μαγνήτη είναι το άθροισμα πεδίων από όλα τα μαγνητισμένα στοιχεία όγκου, τα οποία αποτελούνται από μικρά μαγνητικά δίπολα σε ατομικό επίπεδο. Η άμεση άθροιση όλων αυτών των διπολικών πεδίων θα απαιτούσε τρισδιάστατη ολοκλήρωση μόνο για να ληφθεί το πεδίο ενός μαγνήτη, το οποίο μπορεί να είναι περίπλοκο.
Σε περίπτωση ομοιογενούς μαγνήτισης, το πρόβλημα μπορεί να απλοποιηθεί τουλάχιστον με δύο διαφορετικούς τρόπους, χρησιμοποιώντας το θεώρημα του Stokes. Κατά την ολοκλήρωση κατά την κατεύθυνση της μαγνήτισης, όλα τα δίπολα κατά μήκος της γραμμής ολοκλήρωσης ακυρώνονται μεταξύ τους, εκτός από την τελική επιφάνεια του μαγνήτη. Το πεδίο προκύπτει τότε μόνο από εκείνα τα (μαθηματικά) μαγνητικά φορτία που απλώνονται στις τελικές όψεις του μαγνήτη. Αντίθετα, όταν ενσωματώνονται σε μια μαγνητισμένη περιοχή ορθογώνια προς την κατεύθυνση της μαγνήτισης, τα δίπολα εντός αυτής της περιοχής ακυρώνονται μεταξύ τους, εκτός από την εξωτερική επιφάνεια του μαγνήτη, όπου (μαθηματικά) αθροίζονται σε ένα ρεύμα δακτυλίου. Αυτό ονομάζεται μοντέλο Αμπέρ. Και στα δύο μοντέλα, πρέπει να ληφθούν υπόψη μόνο οι δισδιάστατες κατανομές στην επιφάνεια του μαγνήτη, κάτι που είναι απλούστερο από το αρχικό τρισδιάστατο πρόβλημα.
Μοντέλο Μαγνητικών Φορτίων[Επεξεργασία | επεξεργασία κώδικα]
Το μοντέλο μαγνητικού φορτίου υποθέτει ότι οι μαγνητικές δυνάμεις μεταξύ των μαγνητών οφείλονται σε μαγνητικά φορτία συγκεντρωμένα κυρίως κοντά στους πόλους του μαγνήτη. Αυτό το μοντέλο λειτουργεί ακόμη και κοντά στον μαγνήτη όταν το μαγνητικό πεδίο γίνεται πιο περίπλοκο και εξαρτάται περισσότερο από το λεπτομερές σχήμα και τη μαγνήτιση του μαγνήτη παρά από τη συμβολή του μαγνητικού διπόλου. Επισήμως, το πεδίο μπορεί να εκφραστεί ως πολλαπλή επέκταση: Ένα διπολικό πεδίο, συν ένα τετράπολο πεδίο, συν ένα οκτάπολο, κλπ. Στο μοντέλο Αμπέρ, αυτό μπορεί να είναι πολύ δυσκολο μαθηματικό πρόβλημα.
Υπολογισμός της μαγνητικής δύναμης
Ο υπολογισμός της ελκτικής ή απωθητικής δύναμης μεταξύ δύο μαγνητών είναι, στη γενική περίπτωση, μια πολύ περίπλοκη λειτουργία, καθώς εξαρτάται από το σχήμα, τη μαγνήτιση, τον προσανατολισμό και τον διαχωρισμό των μαγνητών. Το μοντέλο μαγνητικού φορτίου εξαρτάται από κάποια γνώση για το πώς το «μαγνητικό φορτίο» κατανέμεται στους μαγνητικούς πόλους.
1.Δύναμη μεταξύ δύο μαγνητικών πόλων
Αν και οι δύο πόλοι είναι αρκετά μικροί για να αναπαρασταθούν ως μεμονωμένα σημεία, τότε μπορούν να θεωρηθούν ως μαγνητικά φορτία σημείου. Κλασικά, η δύναμη μεταξύ δύο μαγνητικών πόλων δίνεται από: [1]
όπου
Η περιγραφή μέσω των πόλων είναι χρήσιμη για τους σχεδίαστες μαγνήτων που σχεδιάζουν και κατασκευάζουν μαγνήτες σε βιομηχανική η ερευνητική κλίμακα. Οι πραγματικοί μαγνήτες έχουν μια πιο πολυσύνθετη κατανομή πόλων από έναν βορρά και νότο. Επομένως, η υλοποίηση της ιδέας του πόλου δεν είναι απλή. Σε ορισμένες περιπτώσεις, ένας από τους πιο πολύπλοκους τύπους που δίνονται παρακάτω θα είναι πιο χρήσιμος.
2.Δύναμη μεταξύ δύο κοντινών μαγνητισμένων επιφανειών της περιοχής Α
Η μηχανική δύναμη μεταξύ δύο κοντινών μαγνητισμένων επιφανειών μπορεί να υπολογιστεί με την ακόλουθη εξίσωση. Η εξίσωση ισχύει μόνο για περιπτώσεις στις οποίες η επίδραση του περιθωρίου είναι αμελητέα και ο όγκος του διακένου αέρα είναι πολύ μικρότερος από αυτόν του μαγνητισμένου υλικού, η δύναμη για κάθε μαγνητισμένη επιφάνεια είναι: [2] [3] [4]
όπου
Η προέλευση αυτής της εξίσωσης είναι ανάλογη με τη δύναμη μεταξύ δύο κοντινών ηλεκτρικά φορτισμένων επιφανειών [5], η οποία υποθέτει ότι το πεδίο μεταξύ των πλακών είναι ομοιόμορφο.
3.Δύναμη μεταξύ δύο Ραβδόμορφων μαγνητών


Η δύναμη μεταξύ δύο πανομοιότυπων κυλινδρικών μαγνητών ράβδων τοποθετημένων από άκρη σε άκρη σε μεγάλη απόσταση είναι περίπου: [2]
όπου
- B0 είναι η πυκνότηα ροής πολύ κοντά σε κάθε πόλο, σε T,(Τέσλα),
- A είναι το εμβαδόν του κάθε πόλου σε m2,(Τετραγωνικά Μέτρα),
- L είναι το μήκος του κάθε μαγνήτη, σε m,(Μέτρα)
- R είναι η ακτίνα κάθε μαγνήτη σε m, και
- x είναι η απόσταση μεταξύ των μαγνητών, σε m
- σχετίζει την πυκνότητα ροής στον πόλο με τη μαγνήτιση του μαγνήτη.
Σημειώστε ότι αυτή η μαθηματική περιγραφή υποθέτουν κατανομές μαγνητικού φορτίου αντί για μια ομοιόμορφη κατανομή στις τελικές όψεις, κάτι που αποτελεί καλή προσέγγιση μόνο σε σχετικά μεγάλες αποστάσεις. Για ενδιάμεσες αποστάσεις, θα πρέπει να χρησιμοποιούνται αριθμητικές μέθοδοι για μια ακριβέστερη περιγραφή.
4.Δύναμη μεταξύ δύο κυλινδρικών μαγνητών
Για δύο κυλινδρικούς μαγνήτες ακτίνας R και μήκους L η δύναμη μπορεί να υπολογιστεί κάνοντας χρήση ελλειπτικών ολοκληρωμάτων.Έτσι η δύναμη μπορεί να προσεγκιστεί ακόλουθα με την σχέση:
όπου
Το οποίο ταιριάζει με την έκφραση της δύναμης μεταξύ δύο μαγνητικών διπόλων.
Μοντέλο του Αμπέρ[Επεξεργασία | επεξεργασία κώδικα]
Ο γάλλος επιστήμονας Αμπέρ (André Marie Ampère) διαπίστωσε ότι ο μαγνητισμός που παράγεται από μόνιμους μαγνήτες και ο μαγνητισμός που παράγεται από ηλεκτρομαγνητικά αίτια είναι το ίδιο είδος μαγνητισμού.
Εξαιτίας αυτού, η ισχύς ενός μόνιμου μαγνήτη μπορεί να εκφραστεί με τους ίδιους όρους με αυτόν ενός ηλεκτρομαγνήτη.
Η δύναμη του μαγνητισμού ενός ηλεκτρομαγνήτη που είναι ένας επίπεδος βρόχος σύρματος μέσω του οποίου ρέει ένα ηλεκτρικό ρεύμα, που μετριέται σε μια απόσταση που είναι μεγάλη σε σύγκριση με το μέγεθος του βρόχου, είναι ανάλογη με αυτό το ρεύμα και ανάλογη με την επιφάνεια αυτού του βρόχου.
Για να εκφραστεί η ισχύς ενός μόνιμου μαγνήτη με τους όρους ενός ηλεκτρομαγνήτη, ένας μόνιμος μαγνήτης θεωρείται ότι περιέχει μικρούς βρόχους ρεύματος σε ολόκληρο τον όγκο του και στη συνέχεια η μαγνητική ισχύς αυτού του μαγνήτη είναι ανάλογη με το ρεύμα κάθε βρόχου (σε Αμπέρ), και ανάλογη με την επιφάνεια κάθε βρόχου (σε τετραγωνικά μέτρα), και ανάλογο με την πυκνότητα των βρόχων ρεύματος στο υλικό (σε μονάδες ανά κυβικό μέτρο). Αρα η διάσταση του μαγνητισμού ενός μόνιμου μαγνήτη είναι Αμπέρ επί τετραγωνικό μέτρο ανά κυβικό μέτρο, άρα τελικά έχουμε Αμπέρ ανά μέτρο (στο διεθνές σύστημα μονάδων).
Αυτός είναι ο λόγος για τον οποίο το αμπέρ ανά μέτρο είναι η σωστή μονάδα μαγνητισμού, παρόλο που αυτοί οι μικροί βρόχοι ρεύματος δεν υπάρχουν πραγματικά σε έναν μόνιμο μαγνήτη.
Η εγκυρότητα του μοντέλου του Αμπέρ σημαίνει ότι επιτρέπεται να σκεφτούμε το μαγνητικό υλικό σαν να αποτελείται από βρόχους ρεύματος και το συνολικό αποτέλεσμα είναι το άθροισμα της επίδρασης κάθε βρόχου ρεύματος, και έτσι η μαγνητική επίδραση ενός πραγματικού μαγνήτη μπορεί να υπολογιστεί ως το άθροισμα των μαγνητικών επιδράσεων μικροσκοπικών κομματιών μαγνητικού υλικού που βρίσκονται σε μεγάλη απόσταση σε σύγκριση με το μέγεθος κάθε τεμαχίου.
Αυτό είναι πολύ χρήσιμο για τον υπολογισμό μαγνητικού πεδίου δύναμης ενός πραγματικού μαγνήτη. Περιλαμβάνει το άθροισμα μιας μεγάλης ποσότητας μικρών δυνάμεων και δεν πρέπει να το κάνετε με το χέρι, αλλά λόγω της πολυπλοκότητας και τον αριθμό των πράξεων αφήστε τον υπολογιστή σας να το κάνει αυτό για εσάς με την βοήθεια του κατάλληλου λογισμικού. Το μόνο που χρειάζεται να γνωρίζει το πρόγραμμα υπολογιστή είναι η δύναμη μεταξύ μικρών μαγνητών που βρίσκονται σε μεγάλη απόσταση μεταξύ τους.
Σε τέτοιους υπολογισμούς συχνά υποτίθεται ότι κάθε (ίδιο μέγεθος) μικρό κομμάτι μαγνητικού υλικού έχει εξίσου ισχυρό μαγνητισμό, αλλά αυτό δεν είναι πάντα αλήθεια: ένας μαγνήτης που τοποθετείται κοντά σε άλλο μαγνήτη μπορεί να αλλάξει τη μαγνήτιση αυτού του άλλου μαγνήτη. Για τους μόνιμους μαγνήτες αυτό είναι συνήθως μόνο μια μικρή αλλαγή, αλλά αν έχετε έναν ηλεκτρομαγνήτη που αποτελείται από ένα σύρμα τυλιγμένο γύρω από έναν σιδερένιο πυρήνα και φέρετε έναν μόνιμο μαγνήτη κοντά σε αυτόν τον πυρήνα, τότε η μαγνήτιση αυτού του πυρήνα μπορεί να αλλάξει δραστικά (για παράδειγμα, εάν δεν υπάρχει ρεύμα στο σύρμα, ο ηλεκτρομαγνήτης δεν παρουσιάζει μαγνητικές ιδιότητες , αλλά όταν πλησιάζει ο μόνιμος μαγνήτης, ο πυρήνας του ηλεκτρομαγνήτη αποκτά μαγνητικές ιδιότητες μόνιμες η παροδικές εξαρτόμενες από την φύση του υλικού).
Έτσι, το μοντέλο Αμπέρ είναι κατάλληλο για τον υπολογισμό του μαγνητικού πεδίου και τη δύναμης ενός μόνιμου μαγνήτη, αλλά για τους ηλεκτρομαγνήτες μπορεί να είναι καλύτερο να χρησιμοποιηθεί μια προσέγγιση μαγνητικού κυκλώματος.
Μαγνητική αλληλεπίδραση διπόλου-διπόλου[Επεξεργασία | επεξεργασία κώδικα]
Εάν δύο ή περισσότεροι μαγνήτες είναι αρκετά μικροί ή αρκετά απομακρυσμένοι ώστε το σχήμα και το μέγεθός τους να μην είναι σημαντικά τότε και οι δύο μαγνήτες μπορούν να μοντελοποιηθούν ως μαγνητικά δίπολα που έχουν μαγνητικές ροπές m1 και m2. Σε περίπτωση ομοιόμορφα μαγνητισμένων σφαιρικών μαγνητών αυτό το μοντέλο είναι ακριβές ακόμη και σε πεπερασμένο μέγεθος και απόσταση, καθώς το εξωτερικό πεδίο τέτοιων μαγνητών είναι ακριβώς ένα διπολικό πεδίο.
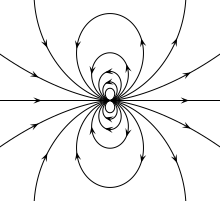
Το μαγνητικό πεδίο ενός μαγνητικού δίπολου σε διανυσματική μορφή είναι:
όπου
- B είναι το πεδίο
- r είναι το διάνυσμα από την θέση του διπόλου έως την θέση όπου το πεδίο μετράται
- r είναι η απόλυτη τιμή του r: η απόσταση από το δίπολο
- είναι το μοναδιαίο διανύσμα παράλληλο στο r;
- m είνα η (διανύσματική) διπολική ροπή
- μ0 είναι η μαγνητική διαπερατότητα του κενού
- δ3 είναι η τρισδιάστατη delta function.[note 1]
Αύτό είναι ακριβώς το πεδίο ενος σημειακού διπόλου , ακριβώς ο διπολικός όρος σε πολυπολική μορφή σε ένα συνηθισμένο πεδίο, και περίπου το πεδίο οποιουδήποτε διπόλου σε μεγάλες αποστάσεις.
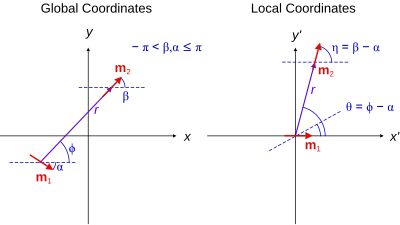

Εάν το σύστημα συντεταγμένων είναι μετατοπισμένο στο κέντρο προς το m1 και περιστραμένο στον άξονα z τα σημεία στην διεύθηνση του m1 τότε η προηγούμενη εξίσωση γίνεται [1]
- ,
όπου η μεταβλητή r και θ είναι μετρημένες στο σύστημα αναφοράς του m1 και κατευθύνεται στο m1 είναι στην κατεύθυνση του άξονα z. Το σύστημα ανφοράς αυτό ονομάζεται Τοπικό και παρουσιαζεται στην εικόνα στα δεξιά.
Η δύναμη που ασκήται σε ένα μαγνητικό δίπολου υπό της παρουσίας ενός άλλου προσδιορίζεται χρησιμοποιώντας το μαγνητικό πεδίο του πρώτου δίπολου που δόθηκε παραπάνω και προσδιορίζοντας τη δύναμη λόγω του μαγνητικού πεδίου στο δεύτερο δίπολο χρησιμοποιώντας την εξίσωση δύναμης που δόθηκε παραπάνω. Χρησιμοποιώντας διανυσματική της μορφή, η δύναμη μεταξύ ενός μαγνητικού δίπολου m1 στο άλλο μαγνητικό δίπολο m2 είναι:
όπου r είναι η διανυσματική απόσταση από το m1 στο m2, με r=||r||. Η δύναμη που ασκήται στο m1 είναι στην αντίθετη κατεύθηνση. Σαν παράδειγμα η μαγνητική δύναμη για δύο σημειακούς μαγνήτες στην κατεύθηνση του άξονα z με απόσταση μεταξύ τους ίση με z είναι:
- , z-κατεύθυνση.
Οι επόμενες σχέσεις , αφορούν εκφράσεις στο παγκόσμιο σύστημα αναφοράς,
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ δ3(r) = 0 εκτός στο r = (0,0,0), έτσι ο όρος αυτός αγνοήται στα πολυπολικά.
- ↑ Schill, R. A. (2003). «General relation for the vector magnetic field of a circular current loop: A closer look». IEEE Transactions on Magnetics 39 (2): 961–967. doi:. Bibcode: 2003ITM....39..961S.


![{\displaystyle F\simeq \left[{\frac {B_{0}^{2}A^{2}\left(L^{2}+R^{2}\right)}{\pi \mu _{0}L^{2}}}\right]\left[{\frac {1}{x^{2}}}+{\frac {1}{(x+2L)^{2}}}-{\frac {2}{(x+L)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc92f379ff8aae485e69ac2ec29922683f34f5bc)





![{\displaystyle \mathbf {F} (\mathbf {r} ,\mathbf {m} _{1},\mathbf {m} _{2})={\frac {3\mu _{0}}{4\pi r^{5}}}\left[(\mathbf {m} _{1}\cdot \mathbf {r} )\mathbf {m} _{2}+(\mathbf {m} _{2}\cdot \mathbf {r} )\mathbf {m} _{1}+(\mathbf {m} _{1}\cdot \mathbf {m} _{2})\mathbf {r} -{\frac {5(\mathbf {m} _{1}\cdot \mathbf {r} )(\mathbf {m} _{2}\cdot \mathbf {r} )}{r^{2}}}\mathbf {r} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78b7d23c669207fabcaa1f93182cccc27f189839)

![{\displaystyle {\begin{aligned}F_{r}(\mathbf {r} ,\alpha ,\beta )&=-{\frac {3\mu _{0}}{4\pi }}{\frac {m_{2}m_{1}}{r^{4}}}\left[2\cos(\phi -\alpha )\cos(\phi -\beta )-\sin(\phi -\alpha )\sin(\phi -\beta )\right]\\F_{\phi }(\mathbf {r} ,\alpha ,\beta )&=-{\frac {3\mu _{0}}{4\pi }}{\frac {m_{2}m_{1}}{r^{4}}}\sin(2\phi -\alpha -\beta )\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44fa313e3fcd5fa92d555d5a7f90fc91616916c4)