Συνάρτηση του Βάιερστρας

Γραφική παράσταση της συνάρτησης Βάιερστρας στο διάστημα [−2, 2]. Όπως ορισμένα άλλα φράκταλ, η συνάρτηση παρουσιάζει αυτοομοιότητα: κάθε μεγέθυνση (κόκκινος κύκλος) είναι παρόμοια με το συνολικό διάγραμμα.

Στα μαθηματικά, η συνάρτηση του Βάιερστρας είναι ένα παράδειγμα συνάρτησης πραγματικών τιμών που είναι συνεχής παντού αλλά δεν είναι διαφορίσιμη. Αποτελεί παράδειγμα μορφοκλασματικής καμπύλης. Πήρε το όνομά της από τον ανακάλυψή της Καρλ Βάιερστρας.

Η συνάρτηση Βάιερστρας διαδραμάτισε ιστορικά το ρόλο μιας παθολογικής συνάρτησης, καθώς είναι το πρώτο δημοσιευμένο παράδειγμα (1872) που επινοήθηκε ειδικά για να αμφισβητήσει την αντίληψη ότι κάθε συνεχής συνάρτηση είναι διαφορίσιμη εκτός από ένα σύνολο απομονωμένων σημείων. Η απόδειξη του Βάιερστρας ότι η συνέχεια δεν συνεπάγεται διαφορισιμότητα σχεδόν παντού έφερε τα πάνω κάτω στα μαθηματικά, ανατρέποντας αρκετές αποδείξεις που βασίζονταν στη γεωμετρική διαίσθηση και σε ασαφείς ορισμούς της ομαλότητας. Αυτοί οι τύποι συναρτήσεων κατακρίθηκαν από τους συγχρόνους: Ο Ανρί Πουανκαρέ τις περιέγραψε ως "τέρατα" και αποκάλεσε το έργο του Βάιερστρας "προσβολή της κοινής λογικής", ενώ ο Σαρλ Ερμίτ έγραψε ότι ήταν μια "θλιβερή μάστιγα". Οι συναρτήσεις ήταν δύσκολο να απεικονιστούν μέχρι την άφιξη των υπολογιστών τον επόμενο αιώνα, και τα αποτελέσματα δεν κέρδισαν ευρεία αποδοχή μέχρι που πρακτικές εφαρμογές, όπως μοντέλα της κίνησης Μπράουν, απαιτούσαν απείρως οδοντωτές συναρτήσεις (σήμερα γνωστές ως φράκταλ καμπύλες).

Κατασκευή

Κινούμενη εικόνα με βάση την αύξηση της τιμής b από 0,1 έως 5.

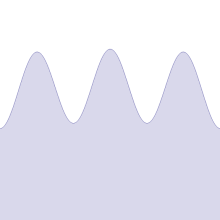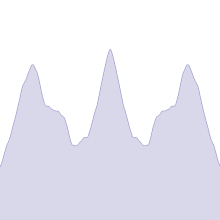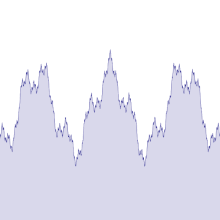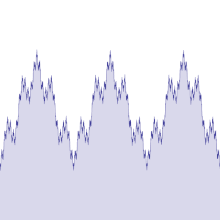
Στην αρχική εργασία του Βάιερστρας, η συνάρτηση ορίστηκε ως σειρά Φουριέ:

$f(x)=\sum _{n=0}^{\infty }a^{n}\cos(b^{n}\pi x),$

Όπου $0<a<1$, $b$ είναι θετικός περιττός ακέραιος αριθμός και

$ab>1+{\frac {3}{2}}\pi .$

Η ελάχιστη τιμή του $b$ για την οποία υπάρχει $0<a<1$ ώστε να ικανοποιούνται αυτοί οι περιορισμοί είναι$b=7$. Αυτή η κατασκευή, μαζί με την απόδειξη ότι η συνάρτηση δεν είναι διαφορίσιμη σε οποιοδήποτε διάστημα, παραδόθηκε για πρώτη φορά από τον Βάιερστρας σε μια εργασία που παρουσιάστηκε στην Βασιλική Ακαδημία Επιστημών στις 18 Ιουλίου 1872.

Παρά το γεγονός ότι δεν είναι ποτέ διαφορίσιμη, η συνάρτηση είναι συνεχής: Δεδομένου ότι οι όροι της άπειρης σειράς που την ορίζει περιορίζονται από ±aⁿ και αυτή έχει πεπερασμένο άθροισμα για 0 < a < 1, η σύγκλιση του αθροίσματος των όρων είναι ομοιόμορφη με το Weierstrass M-test με M_n = aⁿ. Εφόσον κάθε μερικό άθροισμα είναι συνεχές, από το ομοιόμορφο οριακό θεώρημα προκύπτει ότι η f είναι συνεχής. Επιπλέον, αφού κάθε μερικό άθροισμα είναι ομοιόμορφα συνεχές, προκύπτει ότι η f είναι επίσης ομοιόμορφα συνεχής.

Θα περίμενε κανείς ότι μια συνεχής συνάρτηση πρέπει να έχει παράγωγο ή ότι το σύνολο των σημείων στα οποία δεν είναι διαφορίσιμη πρέπει να είναι μετρήσιμα άπειρο ή πεπερασμένο. Σύμφωνα με τον Βάιερστρας στην εργασία του, οι προηγούμενοι μαθηματικοί, συμπεριλαμβανομένου του Γκάους, είχαν συχνά υποθέσει ότι αυτό ίσχυε. Αυτό μπορεί να οφείλεται στο γεγονός ότι είναι δύσκολο να σχεδιάσει ή να απεικονίσει κανείς μια συνεχή συνάρτηση της οποίας το σύνολο των μη διαφορίσιμων σημείων είναι κάτι άλλο από ένα μετρήσιμο σύνολο σημείων. Ανάλογα αποτελέσματα για κατηγορίες συνεχών συναρτήσεων με καλύτερη συμπεριφορά υπάρχουν, για παράδειγμα οι συναρτήσεις Λίπσιτς, των οποίων το σύνολο των μη διαφορίσιμων σημείων πρέπει να είναι ένα μηδενικό σύνολο Λεμπεσγκ (θεώρημα Ραντεμάχερ). Όταν προσπαθούμε να σχεδιάσουμε μια γενική συνεχή συνάρτηση, συνήθως σχεδιάζουμε τη γραφική παράσταση μιας συνάρτησης που είναι Lipschitz ή συμπεριφέρεται ικανοποιητικά.

Η συνάρτηση Βάιερστρας ήταν ένα από τα πρώτα φράκταλ που μελετήθηκαν, αν και ο όρος αυτός δεν χρησιμοποιήθηκε παρά πολύ αργότερα. Η συνάρτηση έχει λεπτομέρεια σε κάθε επίπεδο, οπότε η μεγέθυνση σε ένα κομμάτι της καμπύλης δεν δείχνει ότι πλησιάζει προοδευτικά όλο και περισσότερο σε μια ευθεία γραμμή. Αντίθετα, μεταξύ δύο οποιωνδήποτε σημείων, όσο κοντά κι αν βρίσκονται, η συνάρτηση δεν θα είναι μονότονη.

Ο υπολογισμός της διάστασης Χάουσντορφ D του γραφήματος της κλασικής συνάρτησης Βάιερστρας ήταν ένα ανοιχτό πρόβλημα μέχρι το 2018, ενώ γενικά πιστεύεται ότι D = $2+\log _{b}(a)<2$. Το ότι το D είναι αυστηρά μικρότερο από 2 προκύπτει από τις συνθήκες για τα $a$ και $b$ από παραπάνω. Μόνο μετά από περισσότερα από 30 χρόνια αυτό αποδείχθηκε αυστηρά

Ο όρος συνάρτηση Βάιερστρας χρησιμοποιείται συχνά στην πραγματική ανάλυση για να αναφερθεί σε οποιαδήποτε συνάρτηση με παρόμοιες ιδιότητες και κατασκευή με το αρχικό παράδειγμα του Βάιερστρας. Παραδείγματος χάριν, η συνάρτηση συνημιτόνου μπορεί να αντικατασταθεί στην άπειρη σειρά από μια κατά τμήματα γραμμική συνάρτηση "ζιγκ-ζαγκ". Ο G. H. Hardy έδειξε ότι η συνάρτηση της παραπάνω κατασκευής δεν είναι πουθενά διαφορίσιμη με τις παραδοχές 0 < a < 1, ab ≥ 1.

Συνάρτηση Ρίμαν

Η συνάρτηση του Βάιερστρας βασίζεται στην παλαιότερη συνάρτηση Ρίμαν, η οποία ισχυρίστηκε ότι είναι διαφορίσιμη πουθενά. Περιστασιακά, η συνάρτηση αυτή έχει επίσης ονομαστεί συνάρτηση του Βάιερστρας.

$f(x)=\sum _{n=1}^{\infty }{\frac {\sin(n^{2}x)}{n^{2}}}$

Ενώ ο Μπέρνχαρντ Ρίμαν ισχυριζόταν σθεναρά ότι η συνάρτηση είναι διαφορίσιμη πουθενά, καμία απόδειξη γι' αυτό δεν δημοσιεύτηκε από τον Ρίμαν και ο Βάιερστρας σημείωσε ότι δεν βρήκε καμία απόδειξη που να επιβιώνει είτε στα έγγραφα του Ρίμαν είτε προφορικά από τους μαθητές του.

Το 1916, ο G. H. Χάρντι επιβεβαίωσε ότι η συνάρτηση δεν έχει πεπερασμένη παράγωγο σε οποιαδήποτε τιμή του $\pi x$ όπου το x είναι ανορθολογικό ή είναι ορθολογικό με τη μορφή είτε ${\frac {2A}{4B+1}}$ είτε ${\frac {2A+1}{2B}}$, όπου A και B είναι ακέραιοι αριθμοί. Το 1969, ο Τζόζεφ Γκέρβερ διαπίστωσε ότι η συνάρτηση Ρίμαν έχει ένα καθορισμένο διαφορικό για κάθε τιμή του x που μπορεί να εκφραστεί με τη μορφή ${\frac {2A+1}{2B+1}}\pi$ με ακέραιους A και B, ή ορθολογικούς πολλαπλασιαστές του pi με περιττό αριθμητή και παρονομαστή. Σε αυτά τα σημεία, η συνάρτηση έχει παράγωγο $-{\frac {1}{2}}$.. Το 1971, ο J. Gerver έδειξε ότι η συνάρτηση δεν έχει πεπερασμένο διαφορικό στις τιμές του x που μπορούν να εκφραστούν με τη μορφή ${\frac {2A}{2B+1}}\pi$, ολοκληρώνοντας το πρόβλημα της διαφοροποιησιμότητας της συνάρτησης Ρίμαν.

Καθώς η συνάρτηση Ρίμαν είναι διαφορίσιμη μόνο σε ένα μηδενικό σύνολο σημείων, είναι διαφορίσιμη σχεδόν πουθενά.

Συνέχεια Χόλντερ

Είναι βολικό να γράψουμε τη συνάρτηση Βάιερστρας ισοδύναμα ως εξής

$W_{\alpha }(x)=\sum _{n=0}^{\infty }b^{-n\alpha }\cos(b^{n}\pi x)$

για $\alpha =-{\frac {\ln(a)}{\ln(b)}}$. Τότε η W_α(x) είναι συνεχής κατά Χόλντερ με εκθέτη α, δηλαδή υπάρχει μια σταθερά C τέτοια ώστε

$|W_{\alpha }(x)-W_{\alpha }(y)|\leq C|x-y|^{\alpha }$

για όλα τα x και y. Επιπλέον, η W₁ είναι συνεχής κατά Hölder για όλες τις τάξεις α < 1, αλλά όχι συνεχής κατά Lipschitz.

Πυκνότητα συναρτήσεων που δεν διαφοροποιούνται πουθενά

Αποδεικνύεται ότι η συνάρτηση Βάιερστρας απέχει πολύ από το να είναι ένα μεμονωμένο παράδειγμα: αν και είναι "παθολογική", είναι επίσης "τυπική" των συνεχών συναρτήσεων:

• Με την τοπολογική έννοια: το σύνολο των πουθενά-διαφοροποιήσιμων πραγματικών συναρτήσεων στο [0, 1] έρχεται στο διανυσματικό χώρο C([0, 1]; R) όλων των συνεχών πραγματικών συναρτήσεων στο [0, 1] με την τοπολογία της ομοιόμορφης σύγκλισης.
• Με τη θεωρητική έννοια του μέτρου: όταν ο χώρος C([0, 1]; R) είναι εφοδιασμένος με το κλασικό μέτρο Βίνερ γ, η συλλογή των συναρτήσεων που είναι διαφορίσιμες έστω και σε ένα σημείο του [0, 1] έχει γ-μέτρο μηδέν. Το ίδιο ισχύει ακόμη και αν πάρει κανείς πεπερασμένης διάστασης "φέτες" του C([0, 1]; R), με την έννοια ότι οι πουθενά-διαφοροποιήσιμες συναρτήσεις σχηματίζουν ένα επικρατές υποσύνολο του C([0, 1]; R).

Δημοσιεύσεις

• David, Claire (2018), «Bypassing dynamical systems : A simple way to get the box-counting dimension of the graph of the Weierstrass function», Proceedings of the International Geometry Center (Academy of Sciences of Ukraine) 11 (2): 53–68, doi:10.15673/tmgc.v11i2.1028 
• Falconer, K. (1984), The Geometry of Fractal Sets, Cambridge Tracts in Mathematics, Book 85, Cambridge: Cambridge University Press, ISBN 978-0-521-33705-2, //books.google.com/books?id=-Kwp-GrimCIC 
• Gelbaum, B Bernard R.; Olmstead, John M. H. (2003), Counterexamples in Analysis, Dover Books on Mathematics, Dover Publications, ISBN 978-0-486-42875-8, //books.google.com/books?id=D_XBAgAAQBAJ 
• Hardy, G. H. (1916), «Weierstrass's nondifferentiable function», Transactions of the American Mathematical Society (American Mathematical Society) 17 (3): 301–325, doi:10.2307/1989005, http://www.ams.org/journals/tran/1916-017-03/S0002-9947-1916-1501044-1/S0002-9947-1916-1501044-1.pdf 
• Weierstrass, Karl (18 July 1872), Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzeren einen bestimmten Differentialquotienten besitzen, Königlich Preussische Akademie der Wissenschaften 
  • Weierstrass, Karl (1895), «Über continuirliche Functionen eines reellen Arguments, die für keinen Werth des letzeren einen bestimmten Differentialquotienten besitzen», Mathematische Werke von Karl Weierstrass, 2, Berlin, Germany: Mayer & Müller, σελ. 71–74, //books.google.com/books?id=1FhtAAAAMAAJ&pg=PA71 
  • English translation: Edgar, Gerald A. (1993), «On continuous functions of a real argument that do not possess a well-defined derivative for any value of their argument», Classics on Fractals, Studies in Nonlinearity, Addison-Wesley Publishing Company, σελ. 3–9, ISBN 978-0-201-58701-2 

Δείτε επίσης

• Αναδρομή
• Σύνολο Μάντελμπροτ
• Σύνολο Julia
• Οικοδομήσιμο Σύμπαν