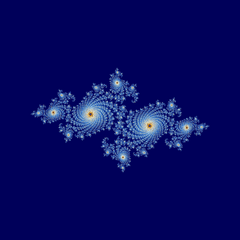
Σύνολο Julia

Μεγέθυνση σε ένα σύνολο Julia στο μιγαδικό επίπεδο z με την μιγαδική πολυωνυμική συνάρτηση δευτέρου βαθμού

p(z)=z^{2}+c

και τις παραμέτρους
c_re = c_im = -0.5251993

Τρισδιάστατες τομές του (τετραδιάστατου) συνόλου Τζούλια μιας συνάρτησης σε Τετραδόνια

Στο πλαίσιο της σύνθετης δυναμικής, ενός κλάδου των μαθηματικών, το σύνολο Julia (Τζούλια)^[1]^[2] και το σύνολο Φατού είναι δύο συμπληρωματικά σύνολα (τα "κορδόνια" του Julia και η "σκόνη" του Φατού) που ορίζονται από μια συνάρτηση. Ανεπίσημα, το σύνολο Φατού της συνάρτησης αποτελείται από τιμές με την ιδιότητα ότι όλες οι κοντινές τιμές συμπεριφέρονται παρόμοια όταν η συνάρτηση επαναλαμβάνεται επανειλημμένα, ενώ το σύνολο Τζούλια αποτελείται από τιμές τέτοιες ώστε μια αυθαίρετα μικρή διαταραχή μπορεί να προκαλέσει ριζικές αλλαγές στην ακολουθία των επαναλαμβανόμενων τιμών της συνάρτησης. Έτσι, η συμπεριφορά της συνάρτησης στο σύνολο Φατού είναι "κανονική", ενώ στο σύνολο Τζούλια η συμπεριφορά του είναι "χαοτική".

Το σύνολο Julia μιας συνάρτησης $f$ συμβολίζεται συνήθως ως $\operatorname {J} (f),$ και το σύνολο Fatou συμβολίζεται ως $\operatorname {F} (f).$ [α] Τα σύνολα αυτά πήραν το όνομά τους από τους Γάλλους μαθηματικούς Γκαστόν Τζούλια^[3] και Πιέρ Φατού^[4], το έργο των οποίων εγκαινίασε τη μελέτη της μιγαδικής δυναμικής στις αρχές του 20ού αιώνα.

Επίσημος ορισμός[Επεξεργασία | επεξεργασία κώδικα]

Έστω $f(z)$ μια μη σταθερή ολομορφική συνάρτηση της σφαίρας Ρίμαν στον ίδιο της τον εαυτό. Τέτοιες συναρτήσεις $f(z)$ είναι ακριβώς οι μη σταθερές μιγαδικές ορθολογικές συναρτήσεις, δηλαδή $f(z)=p(z)/q(z)$ όπου $p(z)$ and $q(z)$ είναι μιγαδικά πολυώνυμα. Ας υποθέσουμε ότι τα p και q δεν έχουν κοινές ρίζες και ότι τουλάχιστον ένα από αυτά έχει βαθμό μεγαλύτερο από 1. Τότε υπάρχει πεπερασμένος αριθμός ανοικτών συνόλων $F_{1},...,F_{r}$ τα οποία είναι αναλλοίωτα από το $f(z)$ και είναι τέτοια ώστε :

Η ένωση των συνόλων $F_{i}$ είναι πυκνή στο επίπεδο και
η $f(z)$ συμπεριφέρεται κανονικά και εξίσου σε κάθε ένα από τα σύνολα $F_{i}$ .

Η τελευταία πρόταση σημαίνει ότι τα άκρα των ακολουθιών των επαναλήψεων που δημιουργούνται από τα σημεία του $F_{i}$ είναι είτε ακριβώς το ίδιο σύνολο, το οποίο είναι τότε ένας πεπερασμένος κύκλος, είτε κύκλοι συνόλων κυκλικής μορφής ή δακτυλιοειδών συνόλων που βρίσκονται συγκεντρωτικά. Στην πρώτη περίπτωση, ο κύκλος είναι "ελκυστικός", στη δεύτερη περίπτωση είναι "ουδέτερος".

Αυτά τα σύνολα $F_{i}$ είναι τα πεδία Φατού της $f(z)$ , και η ένωσή τους είναι το σύνολο Φατού $\operatorname {F} (f)$ της $f(z)$ . Καθένα από τα πεδία Φατού περιέχει τουλάχιστον ένα κρίσιμο σημείο της $f(z)$ , δηλαδή ένα (πεπερασμένο) σημείο z που ικανοποιεί το $f'(z)=0$ , ή $f(z)=\infty$ αν ο βαθμός του αριθμητή p ( z ) p(z) είναι τουλάχιστον διπλάσιος από τον βαθμό του παρονομαστή q ( z ) q(z), ή αν $f(z)=1/g(z)+c$ για κάποιο c και μια ορθολογική συνάρτηση $g(z)$ που ικανοποιεί αυτή τη συνθήκη.

Το συμπλήρωμα του $\operatorname {F} (f)$ είναι το σύνολο Julia $\operatorname {J} (f)$ του $f(z)$ . Αν όλα τα κρίσιμα σημεία είναι προπεριοδικά, δηλαδή δεν είναι περιοδικά αλλά τελικά προσγειώνονται σε έναν περιοδικό κύκλο, τότε το $\operatorname {J} (f)$ είναι όλη η σφαίρα. Διαφορετικά, το $\operatorname {J} (f)$ είναι ένα πουθενά πυκνό σύνολο (είναι χωρίς εσωτερικά σημεία) και ένα μη μετρήσιμο σύνολο (με την ίδια πληθικότητα με τους πραγματικούς αριθμούς). Όπως και το $\operatorname {F} (f)$ , το $\operatorname {J} (f)$ παραμένει αναλλοίωτο από το $f(z)$ , και σε αυτό το σύνολο η επανάληψη είναι απωθητική, που σημαίνει ότι $|f(z)-f(w)|>|z-w|$ για όλα τα w σε μια γειτονιά του z (μέσα στο $\operatorname {J} (f)$ ). Αυτό σημαίνει ότι η $f(z)$ συμπεριφέρεται χαοτικά στο σύνολο Julia. Αν και υπάρχουν σημεία στο σύνολο Julia των οποίων η ακολουθία των επαναλήψεων είναι πεπερασμένη, υπάρχει μόνο ένας μετρήσιμος αριθμός τέτοιων σημείων (και αποτελούν ένα απειροελάχιστο μέρος του συνόλου Julia). Οι ακολουθίες που παράγονται από σημεία εκτός αυτού του συνόλου συμπεριφέρονται χαοτικά, ένα φαινόμενο που ονομάζεται προσδιοριστικό χάος.

Υπήρξε εκτεταμένη έρευνα σχετικά με το σύνολο Φατού και το σύνολο Τζούλια των επαναλαμβανόμενων ορθολογικών συναρτήσεων, γνωστών ως ορθολογικοί χάρτες. Για παράδειγμα, είναι γνωστό ότι το σύνολο Φατού ενός ορθολογικού χάρτη έχει είτε 0, 1, 2 είτε άπειρες συνιστώσες^[5]. Κάθε συνιστώσα του συνόλου Φατού ενός ορθολογικού χάρτη μπορεί να ταξινομηθεί σε μία από τέσσερις διαφορετικές κατηγορίες^[6].

Αντίστοιχες περιγραφές του συνόλου Julia[Επεξεργασία | επεξεργασία κώδικα]

$\operatorname {J} (f)$ είναι το μικρότερο κλειστό σύνολο που περιέχει τουλάχιστον τρία σημεία και είναι πλήρως αναλλοίωτο υπό f.
$\operatorname {J} (f)$ είναι το κλειστό του συνόλου των απωθούμενων περιοδικών σημείων.
Για όλα, εκτός από το πολύ δύο σημεία $\;z\in X\;,$ το σύνολο Julia είναι το σύνολο των οριακών σημείων της πλήρους αντίστροφης τροχιάς $\bigcup _{n}f^{-n}(z).$ (Αυτό υποδηλώνει έναν απλό αλγόριθμο για την απεικόνιση των συνόλων Julia, βλ. παρακάτω).
Αν η f είναι μια ολόκληρη συνάρτηση, τότε $\operatorname {J} (f)$ είναι το όριο του συνόλου των σημείων που συγκλίνουν στο άπειρο υπό επανάληψη.
Αν το f είναι ένα πολυώνυμο, τότε το $\operatorname {J} (f)$ είναι το όριο του γεμάτου συνόλου Τζούλια, δηλαδή τα σημεία των οποίων οι τροχιές κάτω από επαναλήψεις του f παραμένουν περιορισμένες.

Ιδιότητες του συνόλου Julia και του συνόλου Φατού[Επεξεργασία | επεξεργασία κώδικα]

Το σύνολο Julia και το σύνολο Φατού της f είναι και τα δύο πλήρως αναλλοίωτο υπό τις επαναλήψεις της ολομορφικής συνάρτησης f:^[7]

f^{-1}(\operatorname {J} (f))=f(\operatorname {J} (f))=\operatorname {J} (f),

f^{-1}(\operatorname {F} (f))=f(\operatorname {F} (f))=\operatorname {F} (f).

Παραδείγματα[Επεξεργασία | επεξεργασία κώδικα]

Για $f(z)=z^{2}$ το σύνολο Julia είναι ο μοναδιαίος κύκλος και σε αυτό η επανάληψη δίνεται από τον διπλασιασμό των γωνιών (μια πράξη που είναι χαοτική στα σημεία των οποίων το όρισμα δεν είναι ορθολογικό κλάσμα του $2\pi$ ). Υπάρχουν δύο πεδία Φατού: το εσωτερικό και το εξωτερικό του κύκλου, με επανάληψη προς το 0 και το ∞, αντίστοιχα.

Για $g(z)=z^{2}-2$ το σύνολο Julia είναι το ευθύγραμμο τμήμα μεταξύ -2 και 2. Υπάρχει μία περιοχή Φατού τα σημεία που δεν βρίσκονται στο ευθύγραμμο τμήμα επαναλαμβάνονται προς το ∞. (Εκτός από μια μετατόπιση και κλιμάκωση του πεδίου, αυτή η επανάληψη είναι ισοδύναμη με $x\to 4(x-{\tfrac {1}{2}})^{2}$ στο μοναδιαίο διάστημα, το οποίο χρησιμοποιείται συνήθως ως παράδειγμα χαοτικού συστήματος).

Οι συναρτήσεις f και g είναι της μορφής $z^{2}+c$ , όπου c είναι ένας μιγαδικός αριθμός. Για μια τέτοια επανάληψη το σύνολο Julia δεν είναι γενικά μια απλή καμπύλη, αλλά είναι ένα φράκταλ, και για ορισμένες τιμές του c μπορεί να πάρει εκπληκτικές μορφές. Δείτε τις παρακάτω εικόνες.

Για ορισμένες συναρτήσεις f(z) γνωρίζουμε εκ των προτέρων ότι το σύνολο Julia είναι φράκταλ και όχι απλή καμπύλη. Αυτό συμβαίνει λόγω του ακόλουθου αποτελέσματος για τις επαναλήψεις μιας λογικής συνάρτησης:

Θεώρημα - Κάθε περιοχή Φατού έχει το ίδιο όριο, το οποίο κατά συνέπεια είναι το σύνολο Julia.

Αυτό σημαίνει ότι κάθε σημείο του συνόλου Julia είναι ένα σημείο συγκέντρωσης για κάθε έναν από τους τομείς Φατού. Επομένως, αν υπάρχουν περισσότεροι από δύο τομείς Φατού, κάθε σημείο του συνόλου Julia πρέπει να έχει σημεία περισσότερων από δύο διαφορετικών ανοικτών συνόλων απείρως κοντά, πράγμα που σημαίνει ότι το σύνολο Julia δεν μπορεί να είναι μια απλή καμπύλη. Ένα τέτοιο φαινόμενο συμβαίνει, για παράδειγμα, όταν η f(z) είναι η επανάληψη Νεύτων για την επίλυση της εξίσωσης $\;P(z):=z^{n}-1=0~:~n>2\;$ :

f(z)=z-{\frac {P(z)}{P'(z)}}={\frac {\;1+(n-1)z^{n}\;}{nz^{n-1}}}~.

Η εικόνα στα δεξιά δείχνει την περίπτωση n = 3.

Τετραγωνικά πολυώνυμα[Επεξεργασία | επεξεργασία κώδικα]

Ένα πολύ δημοφιλές μιγαδικό δυναμικό σύστημα δίνεται από την οικογένεια των μιγαδικών τετραγωνικών πολυωνύμων, μια ειδική περίπτωση των ορθολογικών χαρτών. Τέτοια τετραγωνικά πολυώνυμα μπορούν να διατυπωθούν ως εξής

f_{c}(z)=z^{2}+c~,

όπου c είναι μια μιγαδική παράμετρος. Ορίστε κάποιο $R>0$ αρκετά μεγάλο ώστε $R^{2}-R\geq |c|.$ (Για παράδειγμα, αν $c$ } είναι στο σύνολο Μάντελμπροτ, τότε $|c|\leq 2,$ οπότε μπορούμε απλά να αφήσουμε $R=2~.$ ) Τότε το συμπληρωμένο σύνολο Julia για αυτό το σύστημα είναι το υποσύνολο του μιγαδικού επιπέδου που δίνεται από τη σχέση

K(f_{c})=\left\{z\in \mathbb {C} :\forall n\in \mathbb {N} ,|f_{c}^{n}(z)|\leq R\right\}~,

όπου $f_{c}^{n}(z)$ είναι η nη επανάληψη της $f_{c}(z).$ Το σύνολο Julia $J(f_{c})$ αυτής της συνάρτησης είναι το όριο της $K(f_{c})$ .

Σύνολα Julia για $z^{2}+0.7885\,e^{ia},$ όπου το a κυμαίνεται από 0 έως $2\pi$
Το βιντεο των συνόλων Julia
Πλήρες σύνολο Julia για f_c, $c = 1 - φ$ , όπου φ είναι χρυσή τομή
Σύνολο Julia για f_c, $c = (φ - 2) + (φ - 1) i = -0.4 + 0.6 i$
Σύνολο Julia για f_c, $c = 0.285 + 0 i$
Σύνολο Julia για f_c, $c = 0.285 + 0.01 i$
Σύνολο Julia για f_c, $c = 0.45 + 0.1428 i$
Σύνολο Julia για f_c, $c = -0.70176 - 0.3842 i$
Σύνολο Julia για f_c, $c = -0.835 - 0.2321 i$
Σύνολο Julia για f_c, $c = -0.8 + 0.156 i$
Σύνολο Julia για f_c, $v c = -0.7269 + 0.1889 i$
Σύνολο Julia για f_c, $c = 0.8 i$
Συλλογή συνόλων Julia τοποθετημένων σε ένα πλέγμα 100 × 100 έτσι ώστε το κέντρο κάθε εικόνας να αντιστοιχεί στην ίδια θέση στο μιγαδικό επίπεδο με την τιμή του συνόλου. Όταν τοποθετείται έτσι, η συνολική εικόνα μοιάζει με ένα φωτογραφικό μωσαϊκό που απεικονίζει ένα σύνολο Μάντελμπροτ.

Το επίπεδο παραμέτρων των τετραγωνικών πολυωνύμων - δηλαδή, το επίπεδο των πιθανών τιμών του c - δίνει το περίφημο σύνολο Μάντελμπροτ. Πράγματι, το σύνολο Μάντελμπροτ ορίζεται ως το σύνολο όλων των c ώστε το $J(f_{c})$ να είναι συνδεδεμένο. Για παραμέτρους εκτός του συνόλου Μάντελμπροτ, το σύνολο Τζούλια είναι ένας χώρος Κάντορ: σε αυτή την περίπτωση αναφέρεται μερικές φορές ως σκόνη Φατού.

Σε πολλές περιπτώσεις, το σύνολο Julia του c μοιάζει με το σύνολο Μάντελμπροτ σε επαρκώς μικρές γειτονιές του c. Αυτό ισχύει, ειδικότερα, για τις λεγόμενες παραμέτρους Μισιούρεβιτς, δηλαδή για τις παραμέτρους c για τις οποίες το κρίσιμο σημείο είναι προ-περιοδικό. Για παράδειγμα:

Στο c = i, το κοντύτερο, μπροστινό δάχτυλο του μπροστινού ποδιού, το σύνολο Julia μοιάζει με διακλαδισμένο κεραυνό.
Στο c = -2, το άκρο της μακράς αγκαθωτής ουράς, το σύνολο Julia είναι ένα ευθύγραμμο τμήμα.

Με άλλα λόγια, τα σύνολα Julia $J(f_{c})$ είναι τοπικά παρόμοια γύρω από τα σημεία Μισιούρεβιτς.^[8]

Γενικεύσεις[Επεξεργασία | επεξεργασία κώδικα]

Ο ορισμός των συνόλων Τζούλια και Φατού μεταφέρεται εύκολα στην περίπτωση ορισμένων χαρτών των οποίων η εικόνα περιέχει το πεδίο ορισμού τους, κυρίως των μερομορφικών συναρτήσεων και των χαρτών πεπερασμένου τύπου του Άνταμ Επστάιν.

Τα σύνολα Julia ορίζονται επίσης συνήθως στη μελέτη της δυναμικής σε πολλές μιγαδικές μεταβλητές.

Ψευδοκώδικας[Επεξεργασία | επεξεργασία κώδικα]

Οι παρακάτω εφαρμογές ψευδοκώδικα κωδικοποιούν αυστηρά τις συναρτήσεις για κάθε φράκταλ. Λάβετε υπόψιν σας την υλοποίηση λειτουργιών μιγαδικών αριθμών, ώστε να είναι πιο δυναμικός και επαναχρησιμοποιήσιμος ο κώδικας.

Ψευδοκώδικας για κανονικά σύνολα Julia[Επεξεργασία | επεξεργασία κώδικα]

f(z)=z^{2}+c

R = escape radius  # choose R > 0 such that R**2 - R >= sqrt(cx**2 + cy**2)

for each pixel (x, y) on the screen, do:   
{
    zx = scaled x coordinate of pixel # (scale to be between -R and R)
       # zx represents the real part of z.
    zy = scaled y coordinate of pixel # (scale to be between -R and R)
       # zy represents the imaginary part of z.

    iteration = 0
    max_iteration = 1000
  
    while (zx * zx + zy * zy < R**2  AND  iteration < max_iteration) 
    {
        xtemp = zx * zx - zy * zy
        zy = 2 * zx * zy  + cy 
        zx = xtemp + cx
    
        iteration = iteration + 1 
    }
  
    if (iteration == max_iteration)
        return black;
    else
        return iteration;
}

Ψευδοκώδικας για σύνολα πολλαπλών Julia[Επεξεργασία | επεξεργασία κώδικα]

f(z)=z^{n}+c

R = escape radius #  choose R > 0 such that R**n - R >= sqrt(cx**2 + cy**2)

for each pixel (x, y) on the screen, do:
{
    zx = scaled x coordinate of pixel # (scale to be between -R and R)
    zy = scaled y coordinate of pixel # (scale to be between -R and R)
  
    iteration = 0
    max_iteration = 1000
  
    while (zx * zx + zy * zy < R**2  AND  iteration < max_iteration) 
    {
        xtmp = (zx * zx + zy * zy) ^ (n / 2) * cos(n * atan2(zy, zx)) + cx;
	    zy = (zx * zx + zy * zy) ^ (n / 2) * sin(n * atan2(zy, zx)) + cy;
	    zx = xtmp;
    
        iteration = iteration + 1
    } 
    if (iteration == max_iteration)
        return black;
    else
        return iteration;
}

Συνάρτηση δυναμικού και πραγματικός αριθμός επανάληψης[Επεξεργασία | επεξεργασία κώδικα]

Το σύνολο Julia για την $f(z)=z^{2}$ είναι ο μοναδιαίος κύκλος και στο εξωτερικό πεδίο Φατού, η συνάρτηση δυναμικού φ(z) ορίζεται από τη σχέση φ(z) = log|z|. Οι ισοδυναμικές γραμμές αυτής της συνάρτησης είναι ομόκεντροι κύκλοι. Καθώς $|f(z)|=|z|^{2}$ έχουμε

\varphi (z)=\lim _{k\to \infty }{\frac {\log |z_{k}|}{2^{k}}},

όπου $z_{k}$ είναι η ακολουθία της επανάληψης που δημιουργείται από το z. Για τη γενικότερη επανάληψη $f(z)=z^{2}+c$ , έχει αποδειχθεί ότι αν το σύνολο Julia είναι συνδεδεμένο (δηλαδή αν το c ανήκει στο (συνηθισμένο) σύνολο Μάντελμπροτ), τότε υπάρχει ένας διχομορφικός χάρτης ψ μεταξύ του εξωτερικού πεδίου Φατού και του εξωτερικού του μοναδιαίου κύκλου έτσι ώστε $|\psi (f(z))|=|\psi (z)|^{2}$ . ^[9] Αυτό σημαίνει ότι η συνάρτηση δυναμικού στην εξωτερική περιοχή Φατού που ορίζεται από αυτή την αντιστοιχία δίνεται από:

\varphi (z)=\lim _{k\to \infty }{\frac {\log |z_{k}|}{2^{k}}}.

Ο τύπος αυτός έχει νόημα και αν το σύνολο Julia δεν είναι συνδεδεμένο, οπότε για όλα τα c μπορούμε να ορίσουμε τη συνάρτηση δυναμικού στο πεδίο Φατού που περιέχει το ∞ με αυτόν τον τύπο. Για μια γενική ορθολογική συνάρτηση f(z) τέτοια ώστε το ∞ να είναι κρίσιμο σημείο και σταθερό σημείο, δηλαδή τέτοια ώστε ο βαθμός m του αριθμητή να είναι τουλάχιστον δύο φορές μεγαλύτερος από τον βαθμό n του παρονομαστή, ορίζουμε τη δυνητική συνάρτηση στο πεδίο Fatou που περιέχει το ∞ από:

\varphi (z)=\lim _{k\to \infty }{\frac {\log |z_{k}|}{d^{k}}},

όπου d = m − n είναι ο βαθμός της ορθολογικής συνάρτησης. ^[10]

Αν το N είναι ένας πολύ μεγάλος αριθμός (π.χ. 10¹⁰⁰), και αν το k είναι ο πρώτος αριθμός επανάληψης τέτοιος ώστε | $z_{k}|>N$ , έχουμε αυτό

{\frac {\log |z_{k}|}{d^{k}}}={\frac {\log(N)}{d^{\nu (z)}}},

για κάποιο πραγματικό αριθμό $\nu (z)$ , ο οποίος θα πρέπει να θεωρηθεί ως ο πραγματικός αριθμός επανάληψης, και έχουμε το εξής:

\nu (z)=k-{\frac {\log(\log |z_{k}|/\log(N))}{\log(d)}},

όπου ο τελευταίος αριθμός βρίσκεται στο διάστημα [0, 1].

Για επανάληψη προς έναν πεπερασμένο κύκλο έλξης τάξης r, έχουμε ότι αν $z^{*}$ είναι ένα σημείο του κύκλου, τότε $f(f(...f(z^{*})))=z^{*}$ (η r-πτυχωτή σύνθεση), και ο αριθμός

\alpha ={\frac {1}{\left|(d(f(f(\cdots f(z))))/dz)_{z=z^{*}}\right|}}\qquad (>1)

είναι η έλξη του κύκλου. Αν w είναι ένα σημείο πολύ κοντά στο $z^{*}$ και w′ είναι το w επαναλαμβανόμενο r φορές, έχουμε το εξής

\alpha =\lim _{k\to \infty }{\frac {|w-z^{*}|}{|w'-z^{*}|}}.

Επομένως ο αριθμός $|z_{kr}-z^{*}|\alpha ^{k}$ είναι σχεδόν ανεξάρτητος του k.. Ορίζουμε τη συνάρτηση δυναμικού στο πεδίο Φατού ως εξής:

\varphi (z)=\lim _{k\to \infty }{\frac {1}{(|z_{kr}-z^{*}|\alpha ^{k})}}.

Εάν ε είναι ένας πολύ μικρός αριθμός και k είναι ο πρώτος αριθμός επανάληψης τέτοιος ώστε $|z_{k}-z^{*}|<\epsilon$ , έχουμε το εξής

\varphi (z)={\frac {1}{(\varepsilon \alpha ^{\nu (z)})}}

για κάποιον πραγματικό αριθμό $\nu (z)$ , ο οποίος θα πρέπει να θεωρηθεί ως ο πραγματικός αριθμός επανάληψης, και έχουμε το εξής:

\nu (z)=k-{\frac {\log(\varepsilon /|z_{k}-z^{*}|)}{\log(\alpha )}}.

Αν η έλξη είναι ∞, δηλαδή ο κύκλος είναι υπερ-ελκυστικός, δηλαδή και πάλι ένα από τα σημεία του κύκλου είναι κρίσιμο σημείο, πρέπει να αντικαταστήσουμε το α με

\alpha =\lim _{k\to \infty }{\frac {\log |w'-z^{*}|}{\log |w-z^{*}|}},

όπου w′ είναι το w επαναλαμβανόμενο r φορές και ο τύπος για το φ(z) από:

\varphi (z)=\lim _{k\to \infty }{\frac {\log(1/|z_{kr}-z^{*}|)}{\alpha ^{k}}}.

Και τώρα ο πραγματικός αριθμός επανάληψης δίνεται από:

\nu (z)=k-{\frac {\log(\log |z_{k}-z^{*}|/\log(\varepsilon ))}{\log(\alpha )}}.

Για τον χρωματισμό πρέπει να έχουμε μια κυκλική κλίμακα χρωμάτων (κατασκευασμένη μαθηματικά, παραδείγματος χάριν) που να περιέχει χρώματα Η αριθμημένα από το 0 έως το Η-1 (Η = 500, ενδεικτικά). Πολλαπλασιάζουμε τον πραγματικό αριθμό $\nu (z)$ με έναν σταθερό πραγματικό αριθμό που καθορίζει την πυκνότητα των χρωμάτων στην εικόνα και παίρνουμε το ολοκληρωτικό μέρος αυτού του αριθμού modulo H.

Ο ορισμός της συνάρτησης δυναμικού και ο τρόπος χρωματισμού μας προϋποθέτουν ότι ο κύκλος είναι ελκτικός, δηλαδή όχι ουδέτερος. Εάν ο κύκλος είναι ουδέτερος, δεν μπορούμε να χρωματίσουμε την περιοχή Fatou με φυσικό τρόπο. Καθώς το τέρμα της επανάληψης είναι μια περιστροφική κίνηση, μπορούμε, λόγου χάρη, να χρωματίσουμε με βάση την ελάχιστη απόσταση από τον κύκλο που αφήνει σταθερό η επανάληψη.

Γραμμές πεδίου[Επεξεργασία | επεξεργασία κώδικα]

Οι ισοδυναμικές γραμμές για την επανάληψη προς το άπειρο

Γραμμές πεδίου για μια επανάληψη της μορφής ${\frac {(1-z^{3}/6)}{(z-z^{2}/2)^{2}}}+c$

Σε κάθε πεδίο Φατού (που δεν είναι ουδέτερο) υπάρχουν δύο συστήματα γραμμών ορθογώνια μεταξύ τους: οι ισοδυναμικές γραμμές (για τη συνάρτηση δυναμικού ή τον πραγματικό αριθμό επανάληψης) και οι γραμμές πεδίου.

Αν χρωματίσουμε το πεδίο Φατού σύμφωνα με τον αριθμό επανάληψης (και όχι τον πραγματικό αριθμό επανάληψης $\nu (z)$ , όπως ορίστηκε στην προηγούμενη ενότητα), οι ζώνες επανάληψης δείχνουν την πορεία των ισοδυναμικών γραμμών. Αν η επανάληψη είναι προς το ∞ (όπως συμβαίνει με την εξωτερική περιοχή Φατού για τη συνήθη επανάληψη $z^{2}+c$ ), μπορούμε εύκολα να δείξουμε την πορεία των γραμμών πεδίου, δηλαδή αλλάζοντας το χρώμα ανάλογα με το αν το τελευταίο σημείο στην ακολουθία της επανάληψης είναι πάνω ή κάτω από τον άξονα x (πρώτη εικόνα), αλλά σε αυτή την περίπτωση (πιο συγκεκριμένα: όταν το πεδίο Fatou είναι υπερ-επικρατές) δεν μπορούμε να σχεδιάσουμε τις γραμμές πεδίου συνεκτικά - τουλάχιστον όχι με τη μέθοδο που περιγράφουμε εδώ. Στην περίπτωση αυτή μια γραμμή πεδίου ονομάζεται επίσης εξωτερική ακτίνα.

Έστω z ένα σημείο στο ελκτικό πεδίο Φατού. Αν επαναλάβουμε το z πολλές φορές, το τέρμα της ακολουθίας επανάληψης είναι ένας πεπερασμένος κύκλος C, και το πεδίο Φατού είναι (εξ ορισμού) το σύνολο των σημείων των οποίων η ακολουθία επανάληψης συγκλίνει προς το C. Οι γραμμές πεδίου ξεκινούν από τα σημεία του C και από το (άπειρο πλήθος) σημείων που επαναλαμβάνονται προς ένα σημείο του C. Και καταλήγουν στο σύνολο Julia σε σημεία που δεν είναι χαοτικά (δηλαδή δημιουργούν έναν πεπερασμένο κύκλο). Έστω r η τάξη του κύκλου C (ο αριθμός των σημείων του) και έστω $z^{*}$ ένα σημείο του C. Έχουμε $f(f(\dots f(z^{*})))=z^{*}$ (η r-πολλαπλή σύνθεση) και ορίζουμε τον μιγαδικό αριθμό α ως εξής

\alpha =(d(f(f(\dots f(z))))/dz)_{z=z^{*}}.

Αν τα σημεία του C είναι $z_{i},i=1,\dots ,r(z_{1}=z^{*})$ , το α είναι το γινόμενο των αριθμών r $f'(z_{i})$ . Ο πραγματικός αριθμός 1/|α| είναι η έλξη του κύκλου, και η παραδοχή μας ότι ο κύκλος δεν είναι ούτε ουδέτερος ούτε υπερ-ελκυστικός, σημαίνει ότι 1 < 1/|α| < ∞. Το σημείο $z^{*}$ είναι σταθερό σημείο για το $f(f(\dots f(z)))$ , και κοντά σε αυτό το σημείο ο χάρτης $f(f(\dots f(z)))$ έχει (σε σχέση με τις γραμμές πεδίου) χαρακτήρα περιστροφής με το επιχείρημα β του α (δηλαδή $\alpha =|\alpha |e^{\beta i}$ ).

Για να χρωματίσουμε το πεδίο Φατού, επιλέξαμε έναν μικρό αριθμό ε και θέσαμε τις ακολουθίες επανάληψης $z_{k}(k=0,1,2,\dots ,z_{0}=z)$ να σταματούν όταν $|z_{k}-z^{*}|<\epsilon$ , και χρωματίζουμε το σημείο z σύμφωνα με τον αριθμό k (ή τον πραγματικό αριθμό επανάληψης, αν προτιμάμε έναν ομαλό χρωματισμό). Αν επιλέξουμε μια κατεύθυνση από το $z^{*}$ που δίνεται από μια γωνία θ, η γραμμή πεδίου που εξέρχεται από το $z^{*}$ σε αυτή τη διεύθυνση αποτελείται από τα σημεία z τέτοια ώστε το επιχείρημα ψ του αριθμού $z_{k}-z^{*}$ να ικανοποιεί τη συνθήκη ότι

\psi -k\beta =\theta \mod \pi .\,

Πράγματι, αν περάσουμε μια ζώνη επανάληψης προς την κατεύθυνση των γραμμών πεδίου (και μακριά από τον κύκλο), ο αριθμός των επαναλήψεων k αυξάνεται κατά 1 και ο αριθμός ψ αυξάνεται κατά β, οπότε ο αριθμός $\psi -k\beta \mod \pi$ είναι σταθερός κατά μήκος της γραμμής πεδίου.

Εικόνες στις γραμμές του πεδίου για μια επανάληψη της φόρμας $z^{2}+c$

Ένας χρωματισμός των γραμμών πεδίου του πεδίου Φατού σημαίνει ότι χρωματίζουμε τους χώρους μεταξύ ζευγών γραμμών πεδίου: επιλέγουμε έναν αριθμό κανονικά τοποθετημένων κατευθύνσεων που ξεκινούν από το $z^{*}$ , και σε κάθε μία από αυτές τις κατευθύνσεις επιλέγουμε δύο κατευθύνσεις γύρω από αυτή τη διεύθυνση. Καθώς μπορεί να συμβεί οι δύο γραμμές πεδίου ενός ζεύγους να μην καταλήγουν στο ίδιο σημείο του συνόλου Julia, οι χρωματισμένες γραμμές πεδίου μας μπορούν να διακλαδίζονται (ατελείωτα) στην πορεία τους προς το σύνολο Julia. Μπορούμε να χρωματίσουμε με βάση την απόσταση από την κεντρική γραμμή της γραμμής πεδίου, και μπορούμε να αναμείξουμε αυτόν τον χρωματισμό με τον συνηθισμένο χρωματισμό. Τέτοιες εικόνες μπορούν να είναι πολύ διακοσμητικές (δεύτερη εικόνα).

Μια χρωματισμένη γραμμή πεδίου (το πεδίο μεταξύ δύο γραμμών πεδίου) διαιρείται από τις ζώνες επανάληψης, και ένα τέτοιο τμήμα μπορεί να τεθεί σε μια ένα προς ένα αντιστοιχία με το μοναδιαίο τετράγωνο: η μία συντεταγμένη είναι (υπολογίζεται από) την απόσταση από μία από τις οριοθετημένες γραμμές πεδίου, η άλλη είναι (υπολογίζεται από) την απόσταση από την εσωτερική από τις οριοθετημένες ζώνες επανάληψης (αυτός ο αριθμός είναι το μη ολοκληρωτικό μέρος του πραγματικού αριθμού επανάληψης). Επομένως, μπορούμε να τοποθετήσουμε εικόνες στις γραμμές πεδίου (τρίτη εικόνα).

Σχεδιάζοντας το σύνολο Julia[Επεξεργασία | επεξεργασία κώδικα]

Δυαδική διάσπαση του εσωτερικού σε περίπτωση εσωτερικής γωνίας 0

Μέθοδοι :

Μέθοδος εκτίμησης απόστασης για το σύνολο Julia (DEM/J)
Μέθοδος αντίστροφης επανάληψης (IIM)

Χρησιμοποιώντας την αντίστροφη επανάληψη (IIM)[Επεξεργασία | επεξεργασία κώδικα]

Μια γραφική παράσταση του συνόλου Julia, που δημιουργήθηκε χρησιμοποιώντας MIIM

Όπως αναφέρθηκε παραπάνω, το σύνολο Julia μπορεί να βρεθεί ως το σύνολο των οριακών σημείων του συνόλου των προ-εικόνων (ουσιαστικά) οποιουδήποτε δεδομένου σημείου. Έτσι μπορούμε να προσπαθήσουμε να σχεδιάσουμε το σύνολο Julia μιας δεδομένης συνάρτησης ως εξής. Ξεκινάμε με οποιοδήποτε σημείο z που γνωρίζουμε ότι βρίσκεται στο σύνολο Julia, όπως ένα απωθητικό περιοδικό σημείο, και υπολογίζουμε όλες τις προ-εικόνες του z κάτω από κάποια υψηλή επανάληψη $f^{n}$ της f.

Δυστυχώς, καθώς ο αριθμός των επαναλαμβανόμενων προ-εικόνων αυξάνεται εκθετικά, αυτό δεν είναι εφικτό υπολογιστικά. Ωστόσο, μπορούμε να προσαρμόσουμε αυτή τη μέθοδο, με παρόμοιο τρόπο όπως η μέθοδος του "τυχαίου παιγνίου" για επαναληπτικό σύστημα συναρτήσεων. Δηλαδή, σε κάθε βήμα, επιλέγουμε τυχαία μία από τις αντίστροφες εικόνες του f.

Για παράδειγμα, για το τετραγωνικό πολυώνυμο f_c, η αντίστροφη επανάληψη περιγράφεται από τη σχέση

z_{n-1}={\sqrt {z_{n}-c}}.

Σε κάθε βήμα επιλέγεται τυχαία μία από τις δύο τετραγωνικές ρίζες.

Ας σημειωθεί ότι ορισμένα τμήματα του συνόλου Julia είναι αρκετά δύσκολο να προσεγγιστούν με τον αντίστροφο αλγόριθμο Julia. Για το λόγο αυτό, πρέπει να τροποποιηθεί ο IIM/J ( ονομάζεται MIIM/J) ή να χρησιμοποιηθούν άλλες μέθοδοι για την παραγωγή καλύτερων εικόνων.

Χρήση DEM/J[Επεξεργασία | επεξεργασία κώδικα]

c=-0.74543+0.11301*i
c=-0.75+0.11*i
c=-0.1+0.651*i
Σύνολο Julia που σχεδιάστηκε με εκτίμηση της απόστασης, η επανάληψη είναι της μορφής $f_{c}(z)=1-z^{2}+{\frac {z^{5}}{2+4z}}+c$
Τρισδιάστατη απεικόνιση του συνόλου Julia με εκτίμηση της αποστάσεως

Καθώς ένα σύνολο Julia είναι απείρως λεπτό, δεν μπορούμε να το σχεδιάσουμε αποτελεσματικά με αντίστροφη επανάληψη από τα εικονοστοιχεία. Θα εμφανίζεται κατακερματισμένο λόγω της μη πρακτικής εξέτασης απείρως πολλών σημείων εκκίνησης. Δεδομένου ότι ο αριθμός των επαναλήψεων αλλάζει έντονα κοντά στο σύνολο Julia, μια μερική λύση είναι να υπονοήσουμε το περίγραμμα του συνόλου από τα πλησιέστερα χρωματικά περιγράμματα, αλλά το σύνολο θα τείνει να φαίνεται θολό.

Ένας καλύτερος τρόπος για να σχεδιάσετε το σύνολο Julia σε ασπρόμαυρο χρώμα είναι να εκτιμήσετε την απόσταση των εικονοστοιχείων (DEM) από το σύνολο και να χρωματίσετε κάθε εικονοστοιχείο του οποίου το κέντρο βρίσκεται κοντά στο σύνολο. Ο τύπος για την εκτίμηση της απόστασης προκύπτει από τον τύπο της συνάρτησης δυναμικού φ(z). Όταν οι ισοδυναμικές γραμμές για την φ(z) βρίσκονται κοντά, ο αριθμός $|\varphi '(z)|$ είναι μεγάλος, και αντίστροφα, επομένως οι ισοδυναμικές γραμμές για τη συνάρτηση $\delta (z)=\varphi (z)/|\varphi '(z)|$ πρέπει να βρίσκονται περίπου κανονικά. Έχει αποδειχθεί ότι η τιμή που βρίσκεται από αυτόν τον τύπο (μέχρι ένα σταθερό παράγοντα) συγκλίνει προς την πραγματική απόσταση για το z που συγκλίνει προς το σύνολο Julia.^[10]

Υποθέτουμε ότι το f(z) είναι ορθολογικό, δηλαδή $f(z)=p(z)/q(z)$ όπου p(z) και q(z) είναι μιγαδικά πολυώνυμα βαθμού m και n, αντίστοιχα, και πρέπει να βρούμε την παράγωγο των παραπάνω εκφράσεων για το φ(z). Και επειδή μεταβάλλεται μόνο το $z_{k}$ , πρέπει να υπολογίσουμε την παράγωγο $z'_{k}$ του $z_{k}$ ως προς z. Καθώς όμως $z_{k}=f(f(\cdots f(z)))$ (η k-πολλαπλή σύνθεση), το $z'_{k}$ είναι το γινόμενο των αριθμών $f'(z_{k})$ , και η ακολουθία αυτή μπορεί να υπολογιστεί αναδρομικά με $z'_{k+1}=f'(z_{k})z'_{k}$ , ξεκινώντας με $z'_{0}=1$ (πριν τον υπολογισμό της επόμενης επανάληψης $z_{k+1}=f(z_{k})$ ).

Για επανάληψη προς το ∞ (πιο συγκεκριμένα όταν $m \geq n + 2$ , έτσι ώστε το ∞ να είναι ένα υπερ-ελκυστικό σταθερό σημείο), έχουμε

|\varphi '(z)|=\lim _{k\to \infty }{\frac {|z'_{k}|}{|z_{k}|d^{k}}},

(d = m - n) και συνεπώς:

\delta (z)=\varphi (z)/|\varphi '(z)|=\lim _{k\to \infty }\log |z_{k}||z_{k}|/|z'_{k}|.\,

Για επανάληψη προς έναν πεπερασμένο ελκυστικό κύκλο (που δεν είναι υπερ-ελκυστικός) που περιέχει το σημείο z* και έχει τάξη r, έχουμε

|\varphi '(z)|=\lim _{k\to \infty }|z'_{kr}|/(|z_{kr}-z^{*}|^{2}\alpha ^{k}),\,

και συνεπώς:

\delta (z)=\varphi (z)/|\varphi '(z)|=\lim _{k\to \infty }|z_{kr}-z^{*}|/|z'_{kr}|.\,

Για έναν εξαιρετικά ελκυστικό κύκλο, ο τύπος έχει ως εξής:

\delta (z)=\lim _{k\to \infty }\log |z_{kr}-z^{*}|^{2}/|z'_{kr}|.\,

Υπολογίζουμε αυτόν τον αριθμό όταν σταματά η επανάληψη. Σημειώστε ότι η εκτίμηση της απόστασης είναι ανεξάρτητη από την έλξη του κύκλου. Αυτό σημαίνει ότι έχει νόημα για υπερβατικές συναρτήσεις "άπειρου βαθμού" (π.χ. sin(z) και tan(z)).

Εκτός από τη σχεδίαση του ορίου, η συνάρτηση απόστασης μπορεί να εισαχθεί ως 3η διάσταση για τη δημιουργία ενός στερεού φρακταλικού τοπίου.

Δημοσιεύσεις[Επεξεργασία | επεξεργασία κώδικα]

Carleson, Lennart· Gamelin, Theodore W. (1993). Complex Dynamics. Springer.
Douady, Adrien; Hubbard, John H. (1984). «Etude dynamique des polynômes complexes». Prépublications mathémathiques d'Orsay 2; [op.cit.]. 4. 1985.
Milnor, J.W. (2006) [1990]. Dynamics in One Complex Variable. Annals of Mathematics Studies. 160 (Third έκδοση). Princeton University Press;
First appeared in as a «Stony Brook IMS Preprint». Αρχειοθετήθηκε από το πρωτότυπο στις 24 Απριλίου 2006. available as Milnor, John W. (1990). «Dynamics in one complex variable: Introductory lectures». arXiv:math.DS/9201272.

Bogomolny, Alexander. «Mandelbrot Set and Indexing of Julia Sets». cut-the-knot. Algebra curriculum.
Demidov, Evgeny (2003). «The Mandelbrot and Julia sets' anatomy».
Beardon, Alan F. (1991). Iteration of Rational Functions. Springer. ISBN 0-387-95151-2.

Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]

Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]

↑ «Julia set - Encyclopedia of Mathematics». encyclopediaofmath.org. Ανακτήθηκε στις 8 Αυγούστου 2023.
↑ «Julia set | mathematics | Britannica». www.britannica.com (στα Αγγλικά). Ανακτήθηκε στις 16 Αυγούστου 2023.
↑ Gaston Julia (1918) "Mémoire sur l'iteration des fonctions rationnelles", Journal de Mathématiques Pures et Appliquées, vol. 8, pages 47–245.
↑ Pierre Fatou (1917) "Sur les substitutions rationnelles", Comptes Rendus de l'Académie des Sciences de Paris, vol. 164, pages 806–808 and vol. 165, pages 992–995.
↑ Beardon, Iteration of Rational Functions, Theorem 5.6.2.
↑ Beardon, Iteration of Rational Functions, Theorem 7.1.1.
↑ Beardon, Iteration of Rational Functions, Θεώρημα 3.2.4.
↑ Tan Lei, "Similarity between the Mandelbrot set and Julia Sets", Communications in Mathematical Physics 134 (1990), pp. 587–617.
↑ Douady, Adrien; Hubbard, John H. (1984). «Etude dynamique des polynômes complexes». Prépublications mathémathiques d'Orsay 2; [op. cit.]. 4. 1985.
↑ ^10,0 ^10,1 Peitgen, Heinz-Otto· Richter Peter (1986). The Beauty of Fractals. Χαϊδελβέργη: Springer-Verlag. ISBN 0-387-15851-0.

[1] «Julia set - Encyclopedia of Mathematics». encyclopediaofmath.org. Ανακτήθηκε στις 8 Αυγούστου 2023.

[2] «Julia set | mathematics | Britannica». www.britannica.com (στα Αγγλικά). Ανακτήθηκε στις 16 Αυγούστου 2023.

[3] Gaston Julia (1918) "Mémoire sur l'iteration des fonctions rationnelles", Journal de Mathématiques Pures et Appliquées, vol. 8, pages 47–245.

[4] Pierre Fatou (1917) "Sur les substitutions rationnelles", Comptes Rendus de l'Académie des Sciences de Paris, vol. 164, pages 806–808 and vol. 165, pages 992–995.

[5] Beardon, Iteration of Rational Functions, Theorem 5.6.2.

[6] Beardon, Iteration of Rational Functions, Theorem 7.1.1.

[7] Beardon, Iteration of Rational Functions, Θεώρημα 3.2.4.

[8] Tan Lei, "Similarity between the Mandelbrot set and Julia Sets", Communications in Mathematical Physics 134 (1990), pp. 587–617.

[9] Douady, Adrien; Hubbard, John H. (1984). «Etude dynamique des polynômes complexes». Prépublications mathémathiques d'Orsay 2; [op. cit.]. 4. 1985.

[Peitgen1986-10] 10,0 ^10,1 Peitgen, Heinz-Otto· Richter Peter (1986). The Beauty of Fractals. Χαϊδελβέργη: Springer-Verlag. ISBN 0-387-15851-0.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]