Σύνολο Κάντορ

Στα μαθηματικά, το σύνολο Κάντορ είναι ένα σύνολο σημείων που βρίσκονται σε ένα μόνο ευθύγραμμο τμήμα, το οποίο έχει ορισμένες μη διαισθητικές ιδιότητες. Ανακαλύφθηκε το 1874 από τον Χένρι Τζον Στίβεν Σμιθ^[1]^[2]^[3]^[4] και εισήχθη από τον Γερμανό μαθηματικό Γκέοργκ Κάντορ το 1883^[5]^[6].

Μελετώντας αυτό το σύνολο, ο Κάντορ και άλλοι βοήθησαν να τεθούν τα θεμέλια της σύγχρονης τοπολογίας σημειακών συνόλων. Η πιο συνηθισμένη κατασκευή είναι το τριμερές σύνολο Κάντορ, το οποίο κατασκευάζεται αφαιρώντας το μεσαίο τρίτο ενός ευθύγραμμου τμήματος και επαναλαμβάνοντας τη διαδικασία με τα υπόλοιπα μικρότερα τμήματα. Ο Κάντορ αναφέρθηκε στην τριμερή κατασκευή μόνο παρεμπιπτόντως, ως παράδειγμα μιας γενικότερης ιδέας, αυτής του τέλειου συνόλου που δεν είναι πουθενά πυκνό.

Σε γενικές γραμμές, στην τοπολογία, ένας χώρος Κάντορ είναι ένας τοπολογικός χώρος ομοιομορφικός με το τριμερές σύνολο Κάντορ (εφοδιασμένος με την τοπολογία του υποχώρου του). Σύμφωνα με ένα θεώρημα του Λ. Ε. Γ. Μπρούβερ, αυτό ισοδυναμεί με το να είναι τέλειος μη-άδειος, συμπαγής μετρήσιμος και μηδενικής διάστασης^[7].

Επέκταση ενός συνόλου Κάντορ. Κάθε σημείο του συνόλου απεικονίζεται εδώ με μια κάθετη γραμμή.

Κατασκευή και τύπος του τριμερούς συνόλου

Το τριμερές σύνολο Κάντορ ${\mathcal {C}}$ δημιουργείται με την επαναληπτική διαγραφή του ανοικτού μεσαίου τρίτου από ένα σύνολο τμημάτων γραμμής. Αρχικά διαγράφουμε το ανοιχτό μεσαίο τρίτο ${\textstyle \left({\frac {1}{3}},{\frac {2}{3}}\right)}$ από το διάστημα $\textstyle \left[0,1\right]$ , αφήνοντας δύο ευθύγραμμα τμήματα: ${\textstyle \left[0,{\frac {1}{3}}\right]\cup \left[{\frac {2}{3}},1\right]}$ . Εν συνεχεία, διαγράφουμε το ανοιχτό μεσαίο τρίτο κάθε ενός από αυτά τα υπόλοιπα τμήματα, αφήνοντας τέσσερα τμήματα γραμμής: ${\textstyle \left[0,{\frac {1}{9}}\right]\cup \left[{\frac {2}{9}},{\frac {1}{3}}\right]\cup \left[{\frac {2}{3}},{\frac {7}{9}}\right]\cup \left[{\frac {8}{9}},1\right]}$ . Το τριμερές σύνολο Κάντορ περιέχει όλα τα σημεία του διαστήματος $[0,1]$ που δεν διαγράφονται σε κανένα βήμα αυτής της άπειρης διαδικασίας. Τα ίδια γεγονότα μπορούν να περιγραφούν αναδρομικά θέτοντας

C_{0}:=[0,1]

και

C_{n}:={\frac {C_{n-1}}{3}}\cup \left({\frac {2}{3}}+{\frac {C_{n-1}}{3}}\right)={\frac {1}{3}}{\bigl (}C_{n-1}\cup \left(2+C_{n-1}\right){\bigr )}

για $n\geq 1$ , έτσι ώστε

{\mathcal {C}}:=

{\color {Blue}\lim _{n\to \infty }C_{n}}

=\bigcap _{n=0}^{\infty }C_{n}=\bigcap _{n=m}^{\infty }C_{n}

for any

m\geq 0

.

Τα έξι πρώτα βήματα αυτής της διαδικασίας απεικονίζονται παρακάτω.

Χρησιμοποιώντας την ιδέα των αυτοομοειδών μετασχηματισμών, $T_{L}(x)=x/3,$ $T_{R}(x)=(2+x)/3$ και $C_{n}=T_{L}(C_{n-1})\cup T_{R}(C_{n-1}),$ οι ρητοί κλειστοί τύποι για το σύνολο Κάντορ είναι^[8]

{\mathcal {C}}=[0,1]\,\setminus \,\bigcup _{n=0}^{\infty }\bigcup _{k=0}^{3^{n}-1}\left({\frac {3k+1}{3^{n+1}}},{\frac {3k+2}{3^{n+1}}}\right)\!,

όπου κάθε μεσαία τρίτη αφαιρείται ως ανοιχτό διάστημα ${\textstyle \left({\frac {3k+1}{3^{n+1}}},{\frac {3k+2}{3^{n+1}}}\right)}$ από το κλειστό διάστημα ${\textstyle \left[{\frac {3k+0}{3^{n+1}}},{\frac {3k+3}{3^{n+1}}}\right]=\left[{\frac {k+0}{3^{n}}},{\frac {k+1}{3^{n}}}\right]}$ που το περιβάλλουν, ή

{\mathcal {C}}=\bigcap _{n=1}^{\infty }\bigcup _{k=0}^{3^{n-1}-1}\left(\left[{\frac {3k+0}{3^{n}}},{\frac {3k+1}{3^{n}}}\right]\cup \left[{\frac {3k+2}{3^{n}}},{\frac {3k+3}{3^{n}}}\right]\right)\!,

όπου το μεσαίο τρίτο ${\textstyle \left({\frac {3k+1}{3^{n}}},{\frac {3k+2}{3^{n}}}\right)}$ του προηγούμενου κλειστού διαστήματος ${\textstyle \left[{\frac {k+0}{3^{n-1}}},{\frac {k+1}{3^{n-1}}}\right]=\left[{\frac {3k+0}{3^{n}}},{\frac {3k+3}{3^{n}}}\right]}$ αφαιρείται από την τομή με το ${\textstyle \left[{\frac {3k+0}{3^{n}}},{\frac {3k+1}{3^{n}}}\right]\cup \left[{\frac {3k+2}{3^{n}}},{\frac {3k+3}{3^{n}}}\right]\!.}$

Αυτή η διαδικασία αφαίρεσης των μεσαίων τρίτων είναι ένα απλό παράδειγμα ενός κανόνα πεπερασμένης υποδιαίρεσης. Το συμπλήρωμα του τριμερούς συνόλου Κάντορ είναι ένα παράδειγμα μορφοκλασματικής αλυσίδας

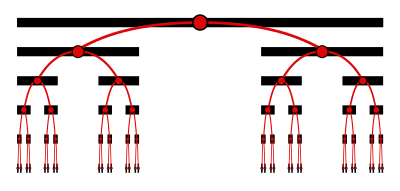
Με αριθμητικούς όρους, το σύνολο Κάντορ αποτελείται από όλους τους πραγματικούς αριθμούς στο μοναδιαίο διάστημα $[0,1]$ που δεν απαιτούν το ψηφίο 1 για να εκφραστούν ως τριμερές κλάσμα (βάση 3). Όπως απεικονίζεται στο παραπάνω διάγραμμα, κάθε σημείο στο σύνολο Κάντορ εντοπίζεται με μοναδικό τρόπο από ένα μονοπάτι σε ένα απείρως βαθύ δυαδικό δέντρο, όπου το μονοπάτι στρίβει αριστερά ή δεξιά σε κάθε επίπεδο ανάλογα με ποια πλευρά ενός διαγραμμένου τμήματος βρίσκεται το σημείο. Αναπαριστώντας κάθε αριστερή στροφή με 0 και κάθε δεξιά στροφή με 2, λαμβάνουμε το τριμερές κλάσμα ενός σημείου.

Η κατασκευή του Μάντελμπροτ με "πήξη"

Στο βιβλίο του με τίτλο Η μορφοκλασματική γεωμετρία της φύσεως, ο μαθηματικός Μπενουά Μάντελμπροτ προτείνει ένα φανταστικό πείραμα σκέψης για να βοηθήσει τους μη μαθηματικούς αναγνώστες να φανταστούν την κατασκευή του ${\mathcal {C}}$ . Η αφήγησή του ξεκινά με τη φαντασία μιας ράβδου, ίσως κατασκευασμένης από ελαφρύ μέταλλο, στην οποία το υλικό της ράβδου "πήζει" καθώς κινείται επαναληπτικά προς τα άκρα της. Καθώς τα τμήματα της ράβδου συρρικνώνονται, γίνονται λεπτά, πυκνά γυμνοσάλιαγκα που τελικά γίνονται πολύ μικρά και αδύναμα για να τα δούμε.

ΠΗΞΗ: Η κατασκευή της ράβδου Κάντορ είναι το αποτέλεσμα μιας διαδικασίας που ονομάζω πήξη. Ξεκινάμε με μια στρογγυλή ράβδο. Είναι καλύτερο να τη φανταστείτε με πολύ χαμηλή πυκνότητα. Στη συνέχεια το υλικό " πήζει " από το κεντρικό τρίτο αυτής της ράβδου προς τα ακραία τρίτα, έτσι ώστε οι θέσεις των τελευταίων να παραμένουν αμετάβλητες. Στη συνέχεια, το υλικό ρέει από το μεσαίο τρίτο κάθε ακραίου τρίτου προς τα ακραία τρίτα του, και ούτω καθεξής μέχρις ότου καταλήξουμε σε έναν απείρως μεγάλο αριθμό απείρως λεπτών σβώλων απείρως υψηλής πυκνότητας. Αυτοί οι γυμνοσάλιαγκες κατανέμονται κατά μήκος της γραμμής με τον πολύ συγκεκριμένο τρόπο που προκαλείται από τη διαδικασία παραγωγής. Σε αυτή την εικόνα, το πήξιμο (που τελικά απαιτεί σφυροκόπημα!) σταματά όταν το πιεστήριο του τυπογραφείου και το μάτι μας σταματήσουν να ακολουθούν- η τελευταία γραμμή δεν διακρίνεται από την προτελευταία: κάθε ένα από τα τελικά της μέρη γίνεται αντιληπτό ως ένας γκρίζος γυμνοσάλιαγκας και όχι ως δύο παράλληλοι μαύροι γυμνοσάλιαγκες.^[9]

Σύνθεση

Λόγω του ότι το σύνολο Κάντορ ορίζεται ως το σύνολο των σημείων που δεν αποκλείονται, η αναλογία (δηλαδή το μέτρο) του μοναδιαίου διαστήματος που απομένει μπορεί να βρεθεί από το συνολικό μήκος που αφαιρείται. Αυτό το σύνολο είναι η γεωμετρική πρόοδος

\sum _{n=0}^{\infty }{\frac {2^{n}}{3^{n+1}}}={\frac {1}{3}}+{\frac {2}{9}}+{\frac {4}{27}}+{\frac {8}{81}}+\cdots ={\frac {1}{3}}\left({\frac {1}{1-{\frac {2}{3}}}}\right)=1.

Έτσι, η αναλογία που απομένει είναι 1 - 1 = 0.

Αυτός ο υπολογισμός υποδηλώνει ότι το σύνολο του Κάντορ δεν μπορεί να περιέχει διαστήματα μη μηδενικού μήκους. Μπορεί να φαίνεται περίεργο το γεγονός ότι κάτι έχει απομείνει - άλλωστε, το άθροισμα των μηκών των διαστημάτων που έχουν αφαιρεθεί είναι ίσο με το μήκος του αρχικού διαστήματος. Εντούτοις, μια πιο προσεκτική ματιά στη διαδικασία αποκαλύπτει ότι πρέπει να μείνει κάτι, αφού η αφαίρεση του "μεσαίου τρίτου" κάθε διαστήματος συνεπάγεται την αφαίρεση ανοικτών συνόλων (σύνολα που δεν περιλαμβάνουν τα άκρα τους). Συνεπώς, η εξάλειψη του δεξιού τμήματος (1/3, 2/3) του αρχικού διαστήματος [0, 1] αφήνει πίσω τα σημεία 1/3 και 2/3. Τα επόμενα βήματα δεν αφαιρούν αυτά τα σημεία (ή οποιαδήποτε άλλα), καθώς τα διαστήματα που αφαιρούνται είναι πάντα εσωτερικά των υπόλοιπων διαστημάτων. Το σύνολο του Κάντορ δεν είναι επομένως άδειο και στην πραγματικότητα περιέχει άπειρο αριθμό σημείων (όπως φαίνεται από την παραπάνω περιγραφή με όρους μονοπατιών σε ένα άπειρο δυαδικό δέντρο).

Ενδέχεται να φανεί ότι απομένουν μόνο τα τελικά σημεία των τμημάτων της κατασκευής, αλλά ούτε αυτό ισχύει. Ο αριθμός 1/4, για παράδειγμα, έχει τη μοναδική τριμερή μορφή 0.020202... = 0.. Βρίσκεται στο κάτω τρίτο, και στο πάνω τρίτο αυτού του τρίτου, και στο κάτω τρίτο αυτού του πάνω τρίτου, και ούτω καθεξής. Αφού δεν βρίσκεται ποτέ σε ένα από τα μεσαία τμήματα, δεν αφαιρείται ποτέ. Παρόλα αυτά, δεν είναι επίσης τελικό σημείο κανενός μεσαίου τμήματος, επειδή δεν είναι πολλαπλάσιο οποιασδήποτε δύναμης του 1/3.^[10] Όλα τα τελικά σημεία των τμημάτων είναι τερματικά τριμερή κλάσματα και περιέχονται στο σύνολο

\left\{x\in [0,1]\mid \exists i\in \mathbb {N} _{0}:x\,3^{i}\in \mathbb {Z} \right\}\qquad {\Bigl (}\subset \mathbb {N} _{0}\,3^{-\mathbb {N} _{0}}{\Bigr )}

το οποίο είναι ένα μετρήσιμο άπειρο σύνολο. Όσον αφορά την πληθικότητα, σχεδόν όλα τα στοιχεία του συνόλου Κάντορ δεν είναι τελικά σημεία διαστημάτων, ούτε ορθολογικά σημεία όπως το 1/4. Ολόκληρο το σύνολο Κάντορ στην πραγματικότητα δεν είναι μετρήσιμο.

Ιδιότητες

Πληθικότητα

Μπορεί να αποδειχθεί ότι υπάρχουν τόσα σημεία που μένουν πίσω σε αυτή τη διαδικασία όσα υπήρχαν στην αρχή, και ότι επομένως, το σύνολο Κάντορ είναι μη μετρήσιμο. Για να το δούμε αυτό, δείχνουμε ότι υπάρχει μια συνάρτηση f από το σύνολο Κάντορ ${\mathcal {C}}$ στο κλειστό διάστημα [0,1] που είναι επιθετική (δηλ. η f απεικονίζει από το ${\mathcal {C}}$ στο [0,1]) έτσι ώστε η καρτελικότητα του ${\mathcal {C}}$ να μην είναι μικρότερη από αυτή του [0,1]. Εφόσον το ${\mathcal {C}}$ είναι υποσύνολο του [0,1], η καρτελικότητά του δεν είναι επίσης μεγαλύτερη, οπότε οι δύο καρτελικότητες πρέπει στην πραγματικότητα να είναι ίσες, σύμφωνα με το θεώρημα Καντόρ-Μπερνστάιν-Σρέντερ.

Για να κατασκευάσετε αυτή τη συνάρτηση, θεωρήστε τα σημεία του διαστήματος [0, 1] με βάση τον συμβολισμό της βάσης 3 (ή τριμερή). Υπενθυμίζουμε ότι τα κατάλληλα τριμερή κλάσματα, ακριβέστερα: τα στοιχεία του ${\bigl (}\mathbb {Z} \setminus \{0\}{\bigr )}\cdot 3^{-\mathbb {N} _{0}}$ , δέχονται περισσότερες από μία αναπαραστάσεις σε αυτόν τον συμβολισμό, όπως παραδείγματος χάριν 1/3, που μπορεί να γραφτεί ως 0,1₃ = 0.1₃, αλλά επίσης και ως 0.0222...₃ = 0.0₃, και 2/3, που μπορεί να γραφεί ως εξής 0.2₃ = 0.2₃ αλλά και ως 0.1222...₃ = 0.1₃.^[11] Όταν αφαιρούμε το μεσαίο τρίτο, αυτό περιέχει τους αριθμούς με τριμερή αριθμητικά στοιχεία της μορφής 0.1xxxxx...₃ όπου xxxxx...₃ είναι αυστηρά μεταξύ 00000...₃ και 22222...₃. Έτσι, οι αριθμοί που απομένουν μετά το πρώτο βήμα αποτελούνται από

Αριθμοί της μορφής 0.0xxxxx...₃ (including 0.022222...₃ = 1/3)
Αριθμοί της μορφής 0.2xxxxx...₃ (including 0.222222...₃ = 1)

Μπορούμε να το συνοψίσουμε αυτό με την εξής φράση: οι αριθμοί με τριμερή αναπαράσταση έτσι ώστε το πρώτο ψηφίο μετά το σημείο ρίζας (radix point) να μην είναι 1 είναι αυτοί που παραμένουν μετά το πρώτο βήμα.

Το δεύτερο βήμα αφαιρεί τους αριθμούς της μορφής 0.01xxxx...₃ και 0.21xxxx...₃, και (με την ανάλογη φροντίδα για τα τελικά σημεία) μπορούμε να συμπεράνουμε ότι οι εναπομείναντες αριθμοί είναι εκείνοι με τριμερή αριθμό όπου κανένα από τα δύο πρώτα ψηφία δεν είναι 1.

Συνεχίζοντας με αυτόν τον τρόπο, για να μην αποκλειστεί κάποιος αριθμός στο βήμα n, θα πρέπει να υπάρχει τριμερής αναπαράσταση της οποίας το nοστό ψηφίο δεν είναι 1. Για να είναι ένας αριθμός στο σύνολο Κάντορ, δεν πρέπει να αποκλείεται σε κανένα βήμα, πρέπει να έχει αριθμητική αναπαράσταση που να αποτελείται αποκλειστικά από 0s και 2s.

Αξίζει να τονιστεί ότι αριθμοί όπως το 1, 1/3 = 0.1₃ και 7/9 = 0.21₃ ανήκουν στο σύνολο Κάντορ, καθώς έχουν τριμερή αριθμητικά στοιχεία που αποτελούνται αποκλειστικά από 0s και 2s: 1 = 0.222...₃ = 0.₃, 1/3 = 0.0222...₃ = 0. 0₃ Όλα αυτά τα τελικά σημεία είναι κατάλληλα τριμερή κλάσματα (στοιχεία του $\mathbb {Z} \cdot 3^{-\mathbb {N} _{0}}$ ) της μορφής form p/q, όπου ο παρονομαστής q είναι δύναμη του 3 όταν το κλάσμα είναι στην μη αναγώγιμη μορφή του. ^[10] Η τριμερής αναπαράσταση αυτών των κλασμάτων τερματίζει (δηλαδή είναι πεπερασμένη) ή - υπενθυμίζουμε από παραπάνω ότι τα ορθά τριμερή κλάσματα έχουν 2 αναπαραστάσεις το καθένα - είναι άπειρη και "τελειώνει" είτε σε άπειρα πολλά επαναλαμβανόμενα 0s είτε σε άπειρα πολλά επαναλαμβανόμενα 2s. Ένα τέτοιο κλάσμα είναι ένα αριστερό οριακό σημείο του ${\mathcal {C}}$ αν η τριμερής αναπαράστασή του δεν περιέχει κανένα 1's και "καταλήγει" σε απείρως πολλά επαναλαμβανόμενα 0s. Ομοίως, ένα κατάλληλο τριμερές κλάσμα είναι δεξιό οριακό σημείο του ${\mathcal {C}}$ αν και πάλι η τριμερής ανάπτυξή του δεν περιέχει κανένα 1's και "καταλήγει" σε απείρως πολλά επαναλαμβανόμενα 2s.

Αυτό το σύνολο τελικών σημείων είναι πυκνό στο ${\mathcal {C}}$ (αλλά όχι πυκνό στο [0, 1]) και αποτελεί ένα μετρήσιμα άπειρο σύνολο. Οι αριθμοί στο ${\mathcal {C}}$ που δεν είναι μη τερματικά σημεία έχουν επίσης μόνο 0s και 2s στην τρισδιάστατη αναπαράστασή τους, αλλά δεν μπορούν να καταλήξουν σε μια άπειρη επανάληψη του ψηφίου 0, ούτε του ψηφίου 2, διότι τότε θα ήταν τερματικό σημείο.

Η συνάρτηση από το ${\mathcal {C}}$ στο [0,1] ορίζεται παίρνοντας τους τρισδιάστατους αριθμούς που αποτελούνται εξ ολοκλήρου από 0s και 2s, αντικαθιστώντας όλα τα 2s με 1s και ερμηνεύοντας την ακολουθία ως δυαδική αναπαράσταση ενός πραγματικού αριθμού. Σε έναν τύπο,

f{\bigg (}\sum _{k\in \mathbb {N} }a_{k}3^{-k}{\bigg )}=\sum _{k\in \mathbb {N} }{\frac {a_{k}}{2}}2^{-k}

όπου

\forall k\in \mathbb {N} :a_{k}\in \{0,2\}.

Για κάθε αριθμό y στο [0,1], η δυαδική αναπαράστασή του μπορεί να μεταφραστεί σε τριπλή αναπαράσταση ενός αριθμού x στο ${\mathcal {C}}$ αντικαθιστώντας όλα τα 1s με 2s.

Με αυτό, f(x) = y έτσι ώστε το y να βρίσκεται στην περιοχή της f. Για παράδειγμα, αν y = 3/5 = 0.100110011001...₂ = 0., γράφουμε x = 0. = 0.200220022002...₃ = 7/10, Συνεπώς, η f είναι επιφανειακή. Ωστόσο, η f δεν είναι εγχυτική - οι τιμές για τις οποίες η f(x) συμπίπτει είναι αυτές που βρίσκονται στα αντίθετα άκρα ενός από τα μεσαία τρίτα που αφαιρούνται. Παραδείγματος χάριν, πάρτε

13 = 0.0₃ (το οποίο είναι ένα δεξιό οριακό σημείο του

{\mathcal {C}}

και ένα αριστερό οριακό σημείο του μεσαίου τρίτου [13, 23]) και

23 = 0.2₃ (το οποίο είναι ένα αριστερό οριακό σημείο του

{\mathcal {C}}

και ένα δεξιό οριακό σημείο του μεσαίου τρίτου [13, 23])

οπότε

{\begin{array}{lcl}f{\bigl (}{}^{1}\!\!/\!_{3}{\bigr )}=f(0.0{\overline {2}}_{3})=0.0{\overline {1}}_{2}=\!\!&\!\!0.1_{2}\!\!&\!\!=0.1{\overline {0}}_{2}=f(0.2{\overline {0}}_{3})=f{\bigl (}{}^{2}\!\!/\!_{3}{\bigr )}.\\&\parallel \\&{}^{1}\!\!/\!_{2}\end{array}}

Έτσι, υπάρχουν τόσα σημεία στο σύνολο Κάντορ όσα και στο διάστημα [0, 1] (το οποίο έχει την αμέτρητη πληθικότητα ${\mathfrak {c}}=2^{\aleph _{0}}$ ).. Ωστόσο, το σύνολο των τελικών σημείων των διαστημάτων που αφαιρούνται είναι μετρήσιμο, οπότε πρέπει να υπάρχουν αμέτρητα πολλοί αριθμοί στο σύνολο Κάντορ που δεν είναι τελικά σημεία διαστημάτων. Όπως σημειώθηκε παραπάνω, ένα παράδειγμα τέτοιου αριθμού είναι το 1/4, το οποίο μπορεί να γραφτεί 0.020202...₃ = 0. σε τριμερή συμβολισμό. Στην πραγματικότητα, δεδομένου οποιουδήποτε $a\in [-1,1]$ , $x,y\in {\mathcal {C}}$ έτσι ώστε $a=y-x$ . Αυτό αποδείχθηκε για πρώτη φορά από τον Ούγκο Στάινχαους το 1917, ο οποίος απέδειξε, μέσω ενός γεωμετρικού επιχειρήματος, τον ισοδύναμο ισχυρισμό ότι $\{(x,y)\in \mathbb {R} ^{2}\mid y=x+a\}\;\cap \;({\mathcal {C}}\times {\mathcal {C}})\neq \emptyset$ για κάθε $a\in [-1,1]$ .^[12] Δεδομένου ότι αυτή η κατασκευή παρέχει μια έγχυση από το $[-1,1]$ to ${\mathcal {C}}\times {\mathcal {C}}$ , έχουμε $|{\mathcal {C}}\times {\mathcal {C}}|\geq |[-1,1]|={\mathfrak {c}}$ ως άμεσο επακόλουθο. Υποθέτοντας ότι $|A\times A|=|A|$ για κάθε άπειρο σύνολο $A$ (μια δήλωση που αποδεικνύεται ότι είναι ισοδύναμη με το αξίωμα της επιλογής από τον Τάρσκι), αυτό προσφέρει μια άλλη απόδειξη ότι $|{\mathcal {C}}|={\mathfrak {c}}$ .

Το σύνολο Κάντορ περιέχει τόσα σημεία όσα και το διάστημα από το οποίο λαμβάνεται, αλλά το ίδιο δεν περιέχει κανένα διάστημα μη μηδενικού μήκους. Οι άρρητοι αριθμοί έχουν την ίδια ιδιότητα, αλλά το σύνολο Κάντορ διαθέτει την πρόσθετη ιδιότητα ότι είναι κλειστό, οπότε δεν είναι καν πυκνό σε κανένα διάστημα, σε αντίθεση με τους άρρητους αριθμούς που είναι πυκνοί σε κάθε διάστημα.

Εικάζεται ότι όλοι οι αλγεβρικοί άρρητοι αριθμοί είναι κανονικοί. Εφόσον τα μέλη του συνόλου Κάντορ δεν είναι κανονικά, αυτό θα σήμαινε ότι όλα τα μέλη του συνόλου Κάντορ είναι είτε ορθολογικοί είτε υπερβατικοί.

Αυτοομοιότητα

Το σύνολο Κάντορ είναι το πρωτότυπο ενός φράκταλ. Είναι αυτοομοειδές, επειδή είναι ίσο με δύο αντίγραφα του εαυτού του, αν κάθε αντίγραφο συρρικνωθεί κατά έναν παράγοντα 3 και μεταφραστεί. Πιο συγκεκριμένα, το σύνολο Κάντορ ισούται με την ένωση δύο συναρτήσεων, του αριστερού και του δεξιού αυτο-ομοιομορφικού μετασχηματισμού του εαυτού του, $T_{L}(x)=x/3$ και $T_{R}(x)=(2+x)/3$ , οι οποίες αφήνουν το σύνολο Κάντορ αναλλοίωτο ως προς τον ομοιομορφισμό: $T_{L}({\mathcal {C}})\cong T_{R}({\mathcal {C}})\cong {\mathcal {C}}=T_{L}({\mathcal {C}})\cup T_{R}({\mathcal {C}}).$

Η επαναλαμβανόμενη επανάληψη των $T_{L}$ και $T_{R}$ μπορεί να απεικονιστεί ως ένα άπειρο δυαδικό δέντρο. Δηλαδή, σε κάθε κόμβο του δέντρου, μπορεί κανείς να εξετάσει το υποδέντρο προς τα αριστερά ή προς τα δεξιά. Λαμβάνοντας το σύνολο $\{T_{L},T_{R}\}$ μαζί με τη σύνθεση συναρτήσεωνν σχηματίζει ένα μονοειδές, το δυαδικό μονοειδές.

Οι αυτομορφισμοί του δυαδικού δέντρου είναι οι υπερβολικές περιστροφές του και δίνονται από τη σπονδυλωτή ομάδα. Έτσι, το σύνολο Κάντορ είναι ένας ομοιογενής χώρος με την έννοια ότι για οποιαδήποτε δύο σημεία $x$ και $y$ στο σύνολο Κάντορ ${\mathcal {C}}$ , υπάρχει ένας ομοιομορφισμός $h:{\mathcal {C}}\to {\mathcal {C}}$ με $h(x)=y$ . Μια ρητή κατασκευή του $h$ μπορεί να περιγραφεί ευκολότερα αν δούμε το σύνολο Κάντορ ως ένα χώρο γινόμενο από μετρήσιμα πολλά αντίγραφα του διακριτού χώρου $\{0,1\}$ . Τότε ο χάρτης $h:\{0,1\}^{\mathbb {N} }\to \{0,1\}^{\mathbb {N} }$ που ορίζεται από τη σχέση $h_{n}(u):=u_{n}+x_{n}+y_{n}\mod 2$ είναι ένας ενορμητικός ομοιομορφισμός που ανταλλάσσει τα $x$ και $y$ .

Νόμος της διατήρησης

Θεωρήθηκε ότι κάποια μορφή νόμου διατήρησης είναι πάντα υπεύθυνη για την κλιμάκωση και την αυτοομοιότητα. Στην περίπτωση του συνόλου Κάντορ μπορεί να διαπιστωθεί ότι η $d_{f}$ th στιγμή (όπου $d_{f}=\ln(2)/\ln(3)$ είναι η μορφοκλασματική διάσταση) όλων των επιζώντων διαστημάτων σε οποιοδήποτε στάδιο της διαδικασίας κατασκευής είναι ίση με μια σταθερά η οποία είναι ένα στην περίπτωση του συνόλου Κάντορ^[13]^[14]. Γνωρίζουμε ότι υπάρχουν $N=2^{n}$ διαστήματα μεγέθους $1/3^{n}$ στο σύστημα κατά το $n$ th βήμα της κατασκευής του. Τότε αν ονομάσουμε τα διαστήματα που επιβιώνουν ως $x_{1},x_{2},\ldots ,x_{2^{n}}$ τότε η $d_{f}$ th στιγμή είναι $x_{1}^{d_{f}}+x_{2}^{d_{f}}+\cdots +x_{2^{n}}^{d_{f}}=1$ αφού $x_{1}=x_{2}=\cdots =x_{2^{n}}=1/3^{n}$ .

Η διάσταση Χάουστορφ του συνόλου Κάντορ είναι ίση με ln(2)/ln(3) ≈ 0,631.

Τοπολογικές και αναλυτικές ιδιότητες

Αν και το "σύνολο" του Κάντορ αναφέρεται συνήθως στο αρχικό σύνολο Κάντορ των μεσαίων τρίτων που περιγράφηκε παραπάνω, οι τοπολόγοι συχνά μιλούν για "ένα" σύνολο Κάντορ, δηλαδή για οποιονδήποτε τοπολογικό χώρο που είναι ομοιομορφικός (τοπολογικά ισοδύναμος) με αυτό.

Όπως δείχνει το παραπάνω αθροιστικό επιχείρημα, το σύνολο Κάντορ είναι αμέτρητο, αλλά έχει μέτρο Λεμπεσγκ 0. Εφόσον το σύνολο Κάντορ είναι το συμπλήρωμα μιας ένωσης ανοικτών συνόλων, το ίδιο είναι ένα κλειστό υποσύνολο των πραγματικών, και επομένως ένας πλήρης μετρικός χώρος. Δεδομένου ότι είναι επίσης πλήρως περιορισμένο, το θεώρημα των Χάινε- Μπορέλ υποδηλώνει ότι πρέπει να είναι συμπαγές.

Για κάθε σημείο του συνόλου Κάντορ και για κάθε αυθαίρετα μικρή γειτονιά του σημείου αυτού, υπάρχει κάποιος άλλος αριθμός με τριαδικό αριθμό που αποτελείται μόνο από 0s και 2s, καθώς και αριθμοί των οποίων οι τριαδικοί αριθμοί περιέχουν 1s. Επομένως, κάθε σημείο του συνόλου Κάντορ είναι ένα σημείο συσσώρευσης (που ονομάζεται επίσης σημείο συστάδας ή οριακό σημείο) του συνόλου Κάντορ, αλλά κανένα δεν είναι εσωτερικό σημείο. Ένα κλειστό σύνολο στο οποίο κάθε σημείο είναι σημείο συσσώρευσης ονομάζεται επίσης τέλειο σύνολο στην τοπολογία, ενώ ένα κλειστό υποσύνολο του διαστήματος χωρίς εσωτερικά σημεία δεν είναι πουθενά πυκνό στο διάστημα.

Κάθε σημείο του συνόλου Κάντορ είναι επίσης σημείο συσσώρευσης του συμπληρώματος του συνόλου Κάντορ.

Για οποιαδήποτε δύο σημεία του συνόλου Κάντορ, θα υπάρχει κάποιο τριπλό ψηφίο στο οποίο θα διαφέρουν - το ένα θα έχει 0 και το άλλο 2. Χωρίζοντας το σύνολο Κάντορ σε "μισά" ανάλογα με την τιμή αυτού του ψηφίου, προκύπτει μια διαμέριση του συνόλου Κάντορ σε δύο κλειστά σύνολα που χωρίζουν τα δύο αρχικά σημεία. Στη σχετική τοπολογία στο σύνολο Κάντορ, τα σημεία έχουν διαχωριστεί από ένα κλειστό σύνολο. Κατά συνέπεια, το σύνολο Κάντορ είναι εντελώς ασύνδετο. Ως ένας συμπαγής εντελώς αποσυνδεδεμένος χώρος Χάουστορφ, το σύνολο Κάντορ είναι ένα παράδειγμα χώρου Στόουν.

Ως τοπολογικός χώρος, το σύνολο Κάντορ είναι φυσικά ομοιομορφικό με το γινόμενο μετρήσιμων αντιγράφων του χώρου $\{0,1\}$ , όπου κάθε αντίγραφο φέρει τη διακριτή τοπολογία. Αυτός είναι ο χώρος όλων των ακολουθιών σε δύο ψηφία

2^{\mathbb {N} }=\{(x_{n})\mid x_{n}\in \{0,1\}{\text{ for }}n\in \mathbb {N} \},

το οποίο μπορεί επίσης να ταυτιστεί με το σύνολο των 2-adic ακεραίων. Η βάση για τα ανοικτά σύνολα της τοπολογίας του προϊόντος είναι τα κυλινδρικά σύνολα- ο ομοιομορφισμός τα αντιστοιχίζει στην τοπολογία υποδιαστήματος που κληρονομεί το σύνολο Κάντορ από τη φυσική τοπολογία στην πραγματική γραμμή. Αυτός ο χαρακτηρισμός του χώρου Κάντορ ως γινόμενο συμπαγών χώρων δίνει μια δεύτερη απόδειξη ότι ο χώρος Κάντορ είναι συμπαγής, μέσω του θεωρήματος Τίχονοφ.

Από τον παραπάνω χαρακτηρισμό, το σύνολο Κάντορ είναι ομοιομορφικό με τους p-adic ακεραίους και, αν αφαιρεθεί ένα σημείο από αυτό, με τους p-adic^[15] αριθμούς.

Το σύνολο Κάντορ είναι ένα υποσύνολο των πραγματικών, που είναι ένας μετρικός χώρος σε σχέση με τη συνηθισμένη μετρική απόστασης- επομένως, το ίδιο το σύνολο Κάντορ είναι ένας μετρικός χώρος, χρησιμοποιώντας την ίδια μετρική. Εναλλακτικά, μπορεί κανείς να χρησιμοποιήσει την p-adic μετρική στο $2^{\mathbb {N} }$ : δεδομένων δύο $(x_{n}),(y_{n})\in 2^{\mathbb {N} }$ , η μεταξύ τους απόσταση είναι $d((x_{n}),(y_{n}))=2^{-k}$ , όπου $k$ είναι ο μικρότερος δείκτης τέτοιος ώστε $x_{k}\neq y_{k}$ ; αν δεν υπάρχει τέτοιος δείκτης, τότε οι δύο ακολουθίες είναι ίδιες και ορίζεται ότι η απόσταση είναι μηδέν. Αυτές οι δύο μετρικές δημιουργούν την ίδια τοπολογία στο σύνολο Κάντορ.

Είδαμε παραπάνω ότι το σύνολο Κάντορ είναι ένας τελείως ασύνδετος τέλειος συμπαγής μετρικός χώρος. Πράγματι, κατά μία έννοια είναι ο μοναδικός: κάθε μη κενός τελείως ασύνδετος τέλεια συμπαγής μετρικός χώρος είναι ομοιομορφικός με το σύνολο Κάντορ. Για περισσότερα σχετικά με τους χώρους που είναι ομοιομορφικοί με το σύνολο Κάντορ, ανατρέξτε στην ενότητα Χώρος Κάντορ.

Το σύνολο Κάντορ θεωρείται μερικές φορές ως "καθολικό" στην κατηγορία των συμπαγών μετρικών χώρων, δεδομένου ότι κάθε συμπαγής μετρικός χώρος είναι μια συνεχής εικόνα του συνόλου Κάντορ.Ωστόσο, αυτή η κατασκευή δεν είναι μοναδική και έτσι το σύνολο Κάντορ δεν είναι καθολικό με την ακριβή κατηγορική έννοια. Η "καθολική" ιδιότητα έχει σημαντικές εφαρμογές στη συναρτησιακή ανάλυση, όπου μερικές φορές είναι γνωστή ως θεώρημα αναπαράστασης για συμπαγείς μετρικούς χώρους^[16].

Για κάθε ακέραιο αριθμό q ≥ 2, η τοπολογία στην ομάδα G = Z_q^ω (το μετρήσιμο άμεσο άθροισμα) είναι διακριτή. Παρόλο που η δυϊκή ομάδα Ποντρτζάγκιν Γ είναι επίσης Z_q^ω, η τοπολογία της Γ είναι συμπαγής. Μπορεί κανείς να δει ότι το Γ είναι εντελώς ασύνδετο και τέλειο - επομένως είναι ομοιομορφικό με το σύνολο Κάντορ. Είναι ευκολότερο να γράψουμε τον ομοιομορφισμό ρητά στην περίπτωση q = 2. (Βλέπε Rudin 1962 σελ 40.)

Ο γεωμετρικός μέσος όρος του συνόλου Κάντορ είναι περίπου 0,274974.^[17]

Μέτρο και πιθανότητα

Το σύνολο Κάντορ μπορεί να θεωρηθεί ως η συμπαγής ομάδα των δυαδικών ακολουθιών και ως τέτοια είναι εφοδιασμένη με ένα φυσικό μέτρο Χαάρ. Όταν ομαλοποιείται έτσι ώστε το μέτρο του συνόλου να είναι 1, είναι ένα πρότυπο μιας άπειρης ακολουθίας ρίψεων νομισμάτων. Επιπλέον, μπορεί κανείς να δείξει ότι το συνηθισμένο μέτρο Λεμπεσγκ στο διάστημα είναι μια εικόνα του μέτρου Χαάρ στο σύνολο Κάντορ, ενώ η φυσική έγχυση στο τριμερές σύνολο είναι ένα κανονικό παράδειγμα ενός μοναδικού μέτρου. Μπορεί επίσης να δειχθεί ότι το μέτρο Χαάρ είναι εικόνα οποιασδήποτε πιθανότητας, καθιστώντας το σύνολο Καντόρ έναν καθολικό χώρο πιθανοτήτων κατά κάποιο τρόπο.

Στη θεωρία μέτρου Λεμπεσγκ, το σύνολο Κάντορ είναι ένα παράδειγμα ενός συνόλου που είναι μη μετρήσιμο και έχει μηδενικό μέτρο^[18]. Αντίθετα, το σύνολο έχει μέτρο Χάουστορφ 1 στη διάστασή του log 2 / log 3.^[19].

Αριθμοί Κάντορ

Αν ορίσουμε έναν αριθμό Κάντορ ως ένα μέλος του συνόλου Κάντορ, τότε ^[20]

Κάθε πραγματικός αριθμός στο [0, 2] είναι το άθροισμα δύο αριθμών Κάντορ.
Μεταξύ δύο οποιωνδήποτε αριθμών Κάντορ υπάρχει ένας αριθμός που δεν είναι αριθμός Κάντορ.

Περιγραφική θεωρία συνόλων

Το σύνολο Κάντορ είναι ένα λιτό σύνολο (ή ένα σύνολο πρώτης κατηγορίας) ως υποσύνολο του [0,1] (αν και όχι ως υποσύνολο του εαυτού του, αφού είναι ένας χώρος Μπαιρ). Το σύνολο Κάντορ αποδεικνύει έτσι ότι οι έννοιες του "μεγέθους" από την άποψη της πληθικότητας, του μέτρου και της (Baire) κατηγορίας δεν χρειάζεται να συμπίπτουν. Όπως και το σύνολο $\mathbb {Q} \cap [0,1]$ , το σύνολο Κάντορ ${\mathcal {C}}$ είναι "μικρό" με την έννοια ότι είναι ένα μηδενικό σύνολο (ένα σύνολο με μέτρο μηδέν) και είναι ένα πενιχρό υποσύνολο του [0,1]. Ωστόσο, σε αντίθεση με το $\mathbb {Q} \cap [0,1]$ , το οποίο είναι μετρήσιμο και έχει "μικρή" πληθικότητα, $\aleph _{0}$ , η πληθικότητα του ${\mathcal {C}}$ είναι ίδια με αυτή του [0,1], του συνεχούς ${\mathfrak {c}}$ , και είναι "μεγάλη" με την έννοια της πληθικότητας. Στην πραγματικότητα, είναι επίσης δυνατό να κατασκευάσουμε ένα υποσύνολο του [0,1] που είναι λιτό αλλά με θετικό μέτρο και ένα υποσύνολο που είναι μη λιτό αλλά με μέτρο μηδέν:^[21]. Παίρνοντας την μετρήσιμη ένωση των "παχιών" συνόλων Κάντορ ${\mathcal {C}}^{(n)}$ του μέτρου $\lambda =(n-1)/n$ (βλέπε Σύνολο Σμιθ-Βολτέρρα-Κάντορ παρακάτω για την κατασκευή), προκύπτει ένα σύνολο ${\textstyle {\mathcal {A}}:=\bigcup _{n=1}^{\infty }{\mathcal {C}}^{(n)}}$ το οποίο έχει θετικό μέτρο (ίσο με 1) αλλά είναι πενιχρό στο [0,1], αφού κάθε ${\mathcal {C}}^{(n)}$ δεν είναι πουθενά πυκνό. Στη συνέχεια, θεωρούμε το σύνολο ${\textstyle {\mathcal {A}}^{\mathrm {c} }=[0,1]\setminus \bigcup _{n=1}^{\infty }{\mathcal {C}}^{(n)}}$ . Αφού ${\mathcal {A}}\cup {\mathcal {A}}^{\mathrm {c} }=[0,1]$ , ${\mathcal {A}}^{\mathrm {c} }$ δεν μπορεί να είναι πενιχρό, αλλά αφού $\mu ({\mathcal {A}})=1$ , ${\mathcal {A}}^{\mathrm {c} }$ πρέπει να έχει μέτρο μηδέν.

Παραλλαγές

Σύνολο Σμιθ-Βολτέρρα-Κάντορ

Δείτε Σύνολο Σμιθ-Βολτέρρα-Κάντορ

Αντί να αφαιρούμε επανειλημμένα το μεσαίο τρίτο κάθε κομματιού όπως στο σύνολο του Κάντορ, θα μπορούσαμε επίσης να συνεχίσουμε να αφαιρούμε οποιοδήποτε άλλο σταθερό ποσοστό (εκτός του 0% και του 100%) του μεσαίου. Στην περίπτωση όπου αφαιρείται το 8/10 του μέσου του διαστήματος, έχουμε μια εξαιρετικά προσιτή περίπτωση - το σύνολο αποτελείται από όλους τους αριθμούς του [0,1] που μπορούν να γραφτούν ως δεκαδικοί που αποτελούνται αποκλειστικά από 0s και 9s. Αν ένα σταθερό ποσοστό αφαιρείται σε κάθε βήμα, τότε το οριακό σύνολο θα έχει μηδενικό μέτρο, αφού το μήκος του υπολοίπου $(1-f)^{n}\to 0$ καθώς $n\to \infty$ κάθε $f$ τέτοιο ώστε $0<f\leq 1$ .

Από την άλλη πλευρά, "παχιά σύνολα Κάντορ" θετικού μέτρου μπορούν να δημιουργηθούν με την αφαίρεση μικρότερων τμημάτων του μέσου του τμήματος σε κάθε επανάληψη. Ως εκ τούτου, μπορεί κανείς να κατασκευάσει σύνολα ομοιόμορφα με το σύνολο Κάντορ που έχουν θετικό μέτρο Λεμπεσγκ ενώ δεν είναι πουθενά πυκνά. Αν ένα διάστημα μήκους $r^{n}$ ( $r\leq 1/3$ ) αφαιρεθεί από το μέσο κάθε τμήματος στην n-οστή επανάληψη, τότε το συνολικό μήκος που αφαιρείται είναι ${\textstyle \sum _{n=1}^{\infty }2^{n-1}r^{n}=r/(1-2r)}$ , και το οριακό σύνολο θα έχει μέτρο Λεμπεσγκ $\lambda =(1-3r)/(1-2r)$ . Έτσι, κατά μία έννοια, το σύνολο Κάντορ μεσαίων-τρίτων είναι μία οριακή περίπτωση με $r=1/3$ . Αν $0<r<1/3$ , τότε το υπόλοιπο θα έχει θετικό μέτρο με $0<\lambda <1$ . Η περίπτωση $r=1/4$ είναι γνωστή ως Σύνολο Σμιθ-Βολτέρρα-Κάντορ, το οποίο έχει μέτρο Λεμπεσγκ $1/2$ .

Στοχαστικό σύνολο Κάντορ

Μπορούμε να τροποποιήσουμε την κατασκευή του συνόλου Κάντορ διαιρώντας το τυχαία αντί ομοιόμορφα. Επιπλέον, για να ενσωματώσουμε το χρόνο, μπορούμε να διαιρούμε μόνο ένα από τα διαθέσιμα διαστήματα σε κάθε βήμα αντί να διαιρούμε όλα τα διαθέσιμα διαστήματα. Στην περίπτωση ενός στοχαστικού τριαδικού συνόλου Κάντορ, η προκύπτουσα διαδικασία μπορεί να περιγραφεί από την ακόλουθη εξίσωση ρυθμού.^[13]^[14]

{\frac {\partial c(x,t)}{\partial t}}=-{\frac {x^{2}}{2}}c(x,t)+2\int _{x}^{\infty }(y-x)c(y,t)\,dy,

και για το στοχαστικό δυαδικό σύνολο Κάντορ ^[23]

{{\partial c(x,t)} \over {\partial t}}=-xc(x,t)+(1+p)\int _{x}^{\infty }c(y,t)\,dy,

όπου $c(x,t)dx$ είναι ο αριθμός των διαστημάτων μεγέθους μεταξύ $x$ και $x+dx$ . Στην περίπτωση του τριαδικού συνόλου Κάντορ η διάσταση του φράκταλ είναι $0,5616$ που είναι μικρότερη από την αντίστοιχη ντετερμινιστική $0,6309$ . Στην περίπτωση του στοχαστικού δυαδικού συνόλου Κάντορ η μορφοκλασματική διάσταση είναι $p$ η οποία είναι και πάλι μικρότερη από εκείνη του ντετερμινιστικού αντίστοιχου $\ln(1+p)/\ln 2$ . Στην περίπτωση του στοχαστικού δυαδικού συνόλου Κάντορ η λύση για το $c(x,t)$ παρουσιάζει δυναμική κλιμάκωση καθώς η λύση του στο μακροχρόνιο όριο είναι $t^{-(1+d_{f})}e^{-xt}$ όπου η fractal διάσταση του στοχαστικού δυαδικού συνόλου Κάντορ $d_{f}=p$ . Σε κάθε περίπτωση, όπως και το τριαδικό σύνολο Κάντορ, η $d_{f}$ th ροπή ( ${\textstyle \int x^{d_{f}}c(x,t)\,dx={\text{constant}}}$ ) του στοχαστικού τριαδικού και δυαδικού συνόλου Κάντορ είναι επίσης διατηρούμενες ποσότητες.

Σκόνη Κάντορ

Η σκόνη Κάντορ είναι μια πολυδιάστατη εκδοχή του συνόλου Κάντορ. Μπορεί να σχηματιστεί παίρνοντας ένα πεπερασμένο καρτεσιανό γινόμενο του συνόλου Κάντορ με τον εαυτό του, καθιστώντας το χώρο Κάντορ. Όπως και το σύνολο Κάντορ, η σκόνη Κάντορ έχει μηδενικό μέτρο^[24]

Ένα διαφορετικό 2D ανάλογο του συνόλου Κάντορ είναι το χαλί Σιερπίνσκι, όπου ένα τετράγωνο χωρίζεται σε εννέα μικρότερα τετράγωνα και το μεσαίο αφαιρείται. Τα υπόλοιπα τετράγωνα στη συνέχεια διαιρούνται περαιτέρω σε εννέα το καθένα και αφαιρείται το μεσαίο, και ούτω καθεξής μέχρι το άπειρο.^[25] Ένα τρισδιάστατο ανάλογο αυτού είναι ο Σπόγγος του Μένγκερ.

Ιστορικές επισημάνσεις

Ο Κάντορ εισήγαγε αυτό που σήμερα ονομάζουμε τριμερές σύνολο Κάντορ ${\mathcal {C}}$ ως παράδειγμα "ενός τέλειου σημειακού συνόλου, το οποίο δεν είναι παντού πυκνό σε οποιοδήποτε διάστημα, όσο μικρό και αν είναι"^[26]^[27]. Ο Κάντορ περιέγραψε το ${\mathcal {C}}$ με όρους τριμερών επεκτάσεων, ως "το σύνολο όλων των πραγματικών αριθμών που δίνονται από τον τύπο: $z=c_{1}/3+c_{2}/3^{2}+\cdots +c_{\nu }/3^{\nu }+\cdots$ όπου οι συντελεστές $c_{\nu }$ παίρνουν αυθαίρετα τις δύο τιμές 0 και 2, και η σειρά μπορεί να αποτελείται από πεπερασμένο ή άπειρο αριθμό στοιχείων. "^[26]

Ένας τοπολογικός χώρος $P$ είναι τέλειος εάν όλα τα σημεία του είναι οριακά σημεία ή, ισοδύναμα, εάν συμπίπτει με το παράγωγο σύνολο $P'$ . Υποσύνολα της πραγματικής γραμμής, όπως το ${\mathcal {C}}$ , μπορούν να θεωρηθούν ως τοπολογικοί χώροι υπό την επαγόμενη τοπολογία υποχώρων^[7].

Ο Κάντορ οδηγήθηκε στη μελέτη των παράγωγων συνόλων από τα αποτελέσματά του σχετικά με τη μοναδικότητα των τριγωνομετρικών σειρών^[27]. Το τελευταίο τον ώθησε σε μεγάλο βαθμό στην ανάπτυξη μιας αφηρημένης, γενικής θεωρίας των άπειρων συνόλων.

Ο Μπενουά Μάντελμπροτ έγραψε αρκετά για τις σκόνες Κάντορ και τη σχέση τους με τα φυσικά φράκταλ και τη στατιστική φυσική^[9]. Επιπλέον, προβληματίστηκε για την αινιγματική ή και ανατρεπτική φύση τέτοιων δομών σε όσους ανήκουν στην κοινότητα των μαθηματικών και της φυσικής. Στο βιβλίο του με τίτλο The Fractal geometry of Nature, περιέγραψε πως "Όταν ξεκίνησα να ασχολούμαι με αυτό το θέμα το 1962, όλοι συμφωνούσαν ότι οι σκόνες Κάντορ είναι τουλάχιστον εξίσου τερατώδεις με τις καμπύλες Κοχ και Πεάνο" και πρόσθεσε ότι "κάθε φυσικός που σέβεται τον εαυτό του αυτόματα απωθήθηκε με την αναφορά του Κάντορ, έτοιμος να τρέξει ένα μίλι μακριά από οποιονδήποτε ισχυριζόταν ότι το ${\mathcal {C}}$ είναι ενδιαφέρον για την επιστήμη"^[9].

Δείτε επίσης

Παραπομπές

↑ Smith, Henry J.S. (1874). «On the integration of discontinuous functions». Proceedings of the London Mathematical Society. First series 6: 140–153. https://zenodo.org/record/1932560.
↑ The "Cantor set" was also discovered by Paul du Bois-Reymond (1831–1889). See du Bois-Reymond, Paul (1880). «Der Beweis des Fundamentalsatzes der Integralrechnung» (στα γερμανικά). Mathematische Annalen 16: footnote on p. 128. http://www.digizeitschriften.de/main/dms/img/?PPN=GDZPPN002245256. . The "Cantor set" was also discovered in 1881 by Vito Volterra (1860–1940). See: Volterra, Vito (1881). «Alcune osservazioni sulle funzioni punteggiate discontinue» (στα it). Giornale di Matematiche 19: 76–86. .
↑ Ferreirós, José (1999). Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics. Basel, Switzerland: Birkhäuser Verlag. σελίδες 162–165. ISBN 9783034850513.
↑ Stewart, Ian (26 Ιουνίου 1997). Does God Play Dice?: The New Mathematics of Chaos. Penguin. ISBN 0140256024.
↑ Cantor, Georg (1883). «Über unendliche, lineare Punktmannigfaltigkeiten V» (στα γερμανικά). Mathematische Annalen 21: 545–591. doi:10.1007/bf01446819. http://www.digizeitschriften.de/main/dms/img/?PPN=GDZPPN002247461. Ανακτήθηκε στις 2011-01-10.
↑ Peitgen, H.-O.· Jürgens, H.· Saupe, D. (2004). Chaos and Fractals: New Frontiers of Science (2nd έκδοση). N.Y., N.Y.: Springer Verlag. σελ. 65. ISBN 978-1-4684-9396-2.
↑ ^7,0 ^7,1 Kechris, Alexander S. (1995). Classical Descriptive Set Theory. Graduate Texts in Mathematics (στα Αγγλικά). 156. Springer New York, NY. σελίδες 31, 35. doi:10.1007/978-1-4612-4190-4. ISBN 978-0-387-94374-9.
↑ Soltanifar, Mohsen (2006). «A Different Description of A Family of Middle-a Cantor Sets». American Journal of Undergraduate Research 5 (2): 9–12. doi:10.33697/ajur.2006.014.
↑ ^9,0 ^9,1 ^9,2 Mandelbrot, Benoit B. (1983). The fractal geometry of nature (Updated and augmented έκδοση). New York. ISBN 0-7167-1186-9. OCLC 36720923.
↑ ^10,0 ^10,1 Belcastro, Sarah-Marie; Green, Michael (January 2001), «The Cantor set contains ${\tfrac {1}{4}}$ ? Really?», The College Mathematics Journal 32 (1): 55, doi:10.2307/2687224
↑ This alternative recurring representation of a number with a terminating numeral occurs in any positional system with Archimedean absolute value.
↑ Carothers, N. L. (2000). Real Analysis. Cambridge: Cambridge University Press. σελίδες 31–32. ISBN 978-0-521-69624-1.
↑ ^13,0 ^13,1 Krapivsky, P. L.; Ben-Naim, E. (1994). «Multiscaling in Stochastic Fractals». Physics Letters A 196 (3–4): 168. doi:10.1016/0375-9601(94)91220-3. Bibcode: 1994PhLA..196..168K.
↑ ^14,0 ^14,1 Hassan, M. K.; Rodgers, G. J. (1995). «Models of fragmentation and stochastic fractals». Physics Letters A 95 (1): 208. doi:10.1016/0375-9601(95)00727-K. Bibcode: 1995PhLA..208...95H.
↑ «P-adic number - Encyclopedia of Mathematics». encyclopediaofmath.org. Ανακτήθηκε στις 2 Δεκεμβρίου 2023.
↑ Willard, Stephen (1968). General Topology. Addison-Wesley. ASIN B0000EG7Q0.
↑ «Cantor Set Geometric Mean».
↑ Irvine, Laura. «Theorem 36: the Cantor set is an uncountable set with zero measure». Theorem of the week. Αρχειοθετήθηκε από το πρωτότυπο στις 15 Μαρτίου 2016. Ανακτήθηκε στις 27 Σεπτεμβρίου 2012.
↑ Falconer, K. J. (24 Ιουλίου 1986). The Geometry of Fractal Sets (PDF). Cambridge University Press. σελίδες 14–15. ISBN 9780521337052.
↑ Schroeder, Manfred (1991). Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. Dover. σελίδες 164–165. ISBN 0486472043.
↑ Gelbaum, Bernard R. (1964). Counterexamples in analysis. Olmsted, John M. H. (John Meigs Hubbell), 1911-1997. San Francisco: Holden-Day. ISBN 0486428753. OCLC 527671.
↑ «Radial Cantor Set».
↑ Hassan, M. K.; Pavel, N. I.; Pandit, R. K.; Kurths, J. (2014). «Dyadic Cantor set and its kinetic and stochastic counterpart». Chaos, Solitons & Fractals 60: 31–39. doi:10.1016/j.chaos.2013.12.010. Bibcode: 2014CSF....60...31H.
↑ Helmberg, Gilbert (2007). Getting Acquainted With Fractals. Walter de Gruyter. σελ. 46. ISBN 978-3-11-019092-2.
↑ Helmberg, Gilbert (2007). Getting Acquainted With Fractals. Walter de Gruyter. σελ. 48. ISBN 978-3-11-019092-2.
↑ ^26,0 ^26,1 Cantor, Georg (2021). «"Foundations of a general theory of sets: A mathematical-philosophical investigation into the theory of the infinite", English translation by James R Meyer». www.jamesrmeyer.com. Footnote 22 in Section 10. Ανακτήθηκε στις 16 Μαΐου 2022.
↑ ^27,0 ^27,1 Fleron, Julian F. (1994). «A Note on the History of the Cantor Set and Cantor Function». Mathematics Magazine 67 (2): 136–140. doi:10.2307/2690689. ISSN 0025-570X. https://www.jstor.org/stable/2690689.

[1] Smith, Henry J.S. (1874). «On the integration of discontinuous functions». Proceedings of the London Mathematical Society. First series 6: 140–153. https://zenodo.org/record/1932560.

[2] The "Cantor set" was also discovered by Paul du Bois-Reymond (1831–1889). See du Bois-Reymond, Paul (1880). «Der Beweis des Fundamentalsatzes der Integralrechnung» (στα γερμανικά). Mathematische Annalen 16: footnote on p. 128. http://www.digizeitschriften.de/main/dms/img/?PPN=GDZPPN002245256. . The "Cantor set" was also discovered in 1881 by Vito Volterra (1860–1940). See: Volterra, Vito (1881). «Alcune osservazioni sulle funzioni punteggiate discontinue» (στα it). Giornale di Matematiche 19: 76–86. .

[3] Ferreirós, José (1999). Labyrinth of Thought: A History of Set Theory and Its Role in Modern Mathematics. Basel, Switzerland: Birkhäuser Verlag. σελίδες 162–165. ISBN 9783034850513.

[4] Stewart, Ian (26 Ιουνίου 1997). Does God Play Dice?: The New Mathematics of Chaos. Penguin. ISBN 0140256024.

[5] Cantor, Georg (1883). «Über unendliche, lineare Punktmannigfaltigkeiten V» (στα γερμανικά). Mathematische Annalen 21: 545–591. doi:10.1007/bf01446819. http://www.digizeitschriften.de/main/dms/img/?PPN=GDZPPN002247461. Ανακτήθηκε στις 2011-01-10.

[6] Peitgen, H.-O.· Jürgens, H.· Saupe, D. (2004). Chaos and Fractals: New Frontiers of Science (2nd έκδοση). N.Y., N.Y.: Springer Verlag. σελ. 65. ISBN 978-1-4684-9396-2.

[:0-7] 7,0 ^7,1 Kechris, Alexander S. (1995). Classical Descriptive Set Theory. Graduate Texts in Mathematics (στα Αγγλικά). 156. Springer New York, NY. σελίδες 31, 35. doi:10.1007/978-1-4612-4190-4. ISBN 978-0-387-94374-9.

[8] Soltanifar, Mohsen (2006). «A Different Description of A Family of Middle-a Cantor Sets». American Journal of Undergraduate Research 5 (2): 9–12. doi:10.33697/ajur.2006.014.

[:3-9] 9,0 ^9,1 ^9,2 Mandelbrot, Benoit B. (1983). The fractal geometry of nature (Updated and augmented έκδοση). New York. ISBN 0-7167-1186-9. OCLC 36720923.

[College-10] 10,0 ^10,1 Belcastro, Sarah-Marie; Green, Michael (January 2001), «The Cantor set contains ${\tfrac {1}{4}}$ ? Really?», The College Mathematics Journal 32 (1): 55, doi:10.2307/2687224

[11] This alternative recurring representation of a number with a terminating numeral occurs in any positional system with Archimedean absolute value.

[12] Carothers, N. L. (2000). Real Analysis. Cambridge: Cambridge University Press. σελίδες 31–32. ISBN 978-0-521-69624-1.

[KBN95-13] 13,0 ^13,1 Krapivsky, P. L.; Ben-Naim, E. (1994). «Multiscaling in Stochastic Fractals». Physics Letters A 196 (3–4): 168. doi:10.1016/0375-9601(94)91220-3. Bibcode: 1994PhLA..196..168K.

[HR95-14] 14,0 ^14,1 Hassan, M. K.; Rodgers, G. J. (1995). «Models of fragmentation and stochastic fractals». Physics Letters A 95 (1): 208. doi:10.1016/0375-9601(95)00727-K. Bibcode: 1995PhLA..208...95H.

[15] «P-adic number - Encyclopedia of Mathematics». encyclopediaofmath.org. Ανακτήθηκε στις 2 Δεκεμβρίου 2023.

[16] Willard, Stephen (1968). General Topology. Addison-Wesley. ASIN B0000EG7Q0.

[17] «Cantor Set Geometric Mean».

[18] Irvine, Laura. «Theorem 36: the Cantor set is an uncountable set with zero measure». Theorem of the week. Αρχειοθετήθηκε από το πρωτότυπο στις 15 Μαρτίου 2016. Ανακτήθηκε στις 27 Σεπτεμβρίου 2012.

[19] Falconer, K. J. (24 Ιουλίου 1986). The Geometry of Fractal Sets (PDF). Cambridge University Press. σελίδες 14–15. ISBN 9780521337052.

[20] Schroeder, Manfred (1991). Fractals, Chaos, Power Laws: Minutes from an Infinite Paradise. Dover. σελίδες 164–165. ISBN 0486472043.

[21] Gelbaum, Bernard R. (1964). Counterexamples in analysis. Olmsted, John M. H. (John Meigs Hubbell), 1911-1997. San Francisco: Holden-Day. ISBN 0486428753. OCLC 527671.

[22] «Radial Cantor Set».

[23] Hassan, M. K.; Pavel, N. I.; Pandit, R. K.; Kurths, J. (2014). «Dyadic Cantor set and its kinetic and stochastic counterpart». Chaos, Solitons & Fractals 60: 31–39. doi:10.1016/j.chaos.2013.12.010. Bibcode: 2014CSF....60...31H.

[24] Helmberg, Gilbert (2007). Getting Acquainted With Fractals. Walter de Gruyter. σελ. 46. ISBN 978-3-11-019092-2.

[25] Helmberg, Gilbert (2007). Getting Acquainted With Fractals. Walter de Gruyter. σελ. 48. ISBN 978-3-11-019092-2.

[:1-26] 26,0 ^26,1 Cantor, Georg (2021). «"Foundations of a general theory of sets: A mathematical-philosophical investigation into the theory of the infinite", English translation by James R Meyer». www.jamesrmeyer.com. Footnote 22 in Section 10. Ανακτήθηκε στις 16 Μαΐου 2022.

[:2-27] 27,0 ^27,1 Fleron, Julian F. (1994). «A Note on the History of the Cantor Set and Cantor Function». Mathematics Magazine 67 (2): 136–140. doi:10.2307/2690689. ISSN 0025-570X. https://www.jstor.org/stable/2690689.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]