Κώδικας του Καίσαρα
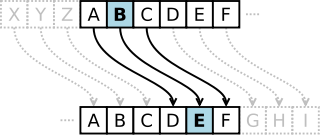
Ο Κώδικας του Καίσαρα είναι μία από τις απλούστερες και πιο γνωστές τεχνικές κρυπτογράφησης. Είναι ένας κώδικας αντικατάστασης στον οποίο κάθε γράμμα του αρχικού κειμένου αντικαθίσταται από κάποιο άλλο γράμμα με σταθερή απόσταση κάθε φορά στο αλφάβητο. Για παράδειγμα, με μετατόπιση 3, το Α θα αντικαθιστούνταν από το Δ, το Β από το Ε, και ούτω καθεξής. Η μέθοδος πήρε το όνομά της από τον Ιούλιο Καίσαρα, ο οποίος τη χρησιμοποιούσε στην προσωπική του αλληλογραφία.
Το βήμα αντικατάστασης που εκτελείται από τον κώδικα του Καίσαρα συχνά ενσωματώνεται ως τμήμα πιο πολύπλοκων αλγορίθμων κρυπτογράφησης, όπως ο κώδικας Vigenère (Βιζενέρ), και έχει ακόμη σύγχρονη εφαρμογή στο σύστημα ROT13. Όπως με όλους τους μονοαλφαβητικούς κώδικες αντικατάστασης, ο κώδικας του Καίσαρα σπάει εύκολα και στη σύγχρονη εφαρμογή του δεν παρέχει ουσιαστικά κάποια ασφάλεια επικοινωνίας.
Παράδειγμα
[Επεξεργασία | επεξεργασία κώδικα]Ο μετασχηματισμός μπορεί να αναπαρασταθεί με παράλληλη παράθεση δύο αλφαβήτων. Τα αλφάβητο κωδικοποίησης είναι το απλό αλφάβητο περιστραμμένο δεξιά ή αριστερά κατά κάποιο αριθμό θέσεων. Για παράδειγμα ακολουθεί ένας κώδικας του Καίσαρα που χρησιμοποιεί αριστερή περιστροφή τριών θέσεων (η παράμετρος μετατόπισης, εδώ 3, χρησιμοποιείται ως κλειδί):
Απλό: ΑΒΓΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩ Κώδικας: ΔΕΖΗΘΙΚΛΜΝΞΟΠΡΣΤΥΦΧΨΩΑΒΓ
Όταν γίνεται κρυπτογράφηση, αναζητείται κάθε γράμμα της «απλής» γραμμής και γράφεται το αντίστοιχο γράμμα από την γραμμή του «κώδικα». Η αποκρυπτογράφηση γίνεται με την αντίστροφη φορά.
Κρυπτογραφημένο κείμενο: ΛΔΠΔΧΣΦ ΘΜΠΔΜ ΣΜ ΝΔΥΖΘΦ ΤΣΨ ΑΧΨΤΜΣΨΠΧΔΜ Απλό κείμενο: θάνατος είναι οι κάργες που χτυπιούνται
Η κρυπτογράφηση μπορεί να αναπαρασταθεί με την χρήση αριθμητικής υπολοίπων αν πρώτα μετασχηματιστούν τα γράμματα σε αριθμούς, σύμφωνα με τον κανόνα, Α = 0, Β = 1,.... Ω = 23.[1] Η κρυπτογράφηση ενός γράμματος με μετατόπιση n μπορεί να περιγραφεί μαθηματικώς ως,[2]
Η αποκρυπτογράφηση γίνεται αναλόγως,
(Υπάρχουν διαφορετικοί ορισμοί για την πράξη modulo. Στα παραπάνω το αποτέλεσμα βρίσκεται στο εύρος 0...23. Ήτοι, αν x+n ή x-n δεν βρίσκονται στο εύρος 0...23, αφαιρείται ή προστίθεται 24.)
Η αντικατάσταση παραμένει η ίδια σε όλο το μήνυμα, έτσι ο κώδικας ταξινομείται ως μονοαλφαβητικής αντικατάστασης, σε αντίθεση με τους κώδικες πολυαλφαβητικής αντικατάστασης.
Ιστορία και χρήση
[Επεξεργασία | επεξεργασία κώδικα]
Ο κώδικας του Καίσαρα πήρε το όνομά του από τον Ιούλιο Καίσαρα, ο οποίος, σύμφωνα με τον Σουητώνιο, τον χρησιμοποιούσε με μετατόπιση τριών θέσεων ώστε να προστατεύσει μηνύματα στρατιωτικής σημασίας. Ενώ η πρώτη καταγεγραμμένη χρήση είναι για τον Καίσαρα, είναι γνωστό ότι χρησιμοποιήθηκαν και άλλοι κώδικες αντικατάστασης νωρίτερα.
Αν είχε κάτι εμπιστευτικό να πει, το έγραφε κωδικοποιημένο, δηλαδή αλλάζοντας την σειρά των γραμμάτων του αλφαβήτου, ώστε ούτε μία λέξη να μην μπορεί να διαβαστεί. Αν οποιοσδήποτε επιθυμεί να τα αποκωδικοποιήσει και να κατανοήσει το νόημα, πρέπει πρώτα να αντικαταστήσει το τέταρτο γράμμα του αλφαβήτου, δηλαδή το D, με το A και να κάνει το ίδιο με τα υπόλοιπα.
— Σουητώνιος, Η ζωή του Ιούλιου Καίσαρα 56
Ο ανιψιός του, Αύγουστος, επίσης χρησιμοποιούσε τον κώδικα, με δεξιά μετατόπιση όμως ενός, και δεν γύριζε στην αρχή του αλφαβήτου:
Όποτε έγραφε κρυπτογραφημένα, έγραφε B για A, C για B, και τα υπόλοιπα γράμματα βάση της ίδιας αρχής, χρησιμοποιώντας όμως AA στη θέση του Z.
— Σουητώνιος, Η ζωή του Αυγούστου 88
Υπάρχουν στοιχεία ότι ο Ιούλιος Καίσαρας χρησιμοποιούσε και πιο πολύπλοκα συστήματα,[3] και ένας συγγραφέας, ο Αύλος Γέλλιος, αναφέρεται σε μία (σήμερα χαμένη) διατριβή για την κρυπτογραφία:
Υπάρχει ακόμα μία μάλλον εφευρετικώς γραμμένη διατριβή από τον γραμματικό Πρόβο σχετικά με το μυστικό νόημα των γραμμάτων στη σύνθεση των επιστολών του Καίσαρα.
— Αύλος Γέλλιος, Αττικαί νύκτες 17.9.1–5
Είναι άγνωστο το πόσο αποτελεσματικός ήταν ο κώδικας του Καίσαρα τον καιρό του, είναι όμως πιθανό ότι ήταν αρκετά ασφαλής, κυρίως επειδή οι περισσότεροι εχθροί του Καίσαρα ήταν αναλφάβητοι και οι υπόλοιποι θα υπέθεταν ότι τα μηνύματα ήταν γραμμένα σε μία άγνωστη ξένη γλώσσα.[4] Δεν υπάρχουν καταγραφές για τεχνικές λύσης κωδίκων απλής αντικατάστασης. Οι παλαιότερες σωζόμενες καταγραφές χρονολογούνται στον 9ο αιώνα στα έργα του Άραβα Αλ Κιντί ο οποίος ανακάλυψε την μέθοδο ανάλυσης συχνοτήτων.[5]
Τον 19ο αιώνα, το τμήμα των προσωπικών διαφημίσεων των εφημερίδων χρησιμοποιούνταν για την ανταλλαγή κρυπτογραφημένων μηνυμάτων με απλούς κώδικες. Ο Ντέιβιντ Καν (1967) περιγράφει παραδείγματα εραστών που χρησιμοποιούσαν κρυπτογραφημένα με τον κώδικα του Καίσαρα μηνύματα για να επικοινωνήσουν μέσω των The Times.[6] Ακόμα και τόσο πρόσφατα όσο το 1915, ο κώδικας του Καίσαρα χρησιμοποιήθηκε από τον Ρωσικό στρατό σε αντικατάσταση πιο πολύπλοκων κωδίκων, οι οποίοι ήταν πολύ δύσκολοι για να εξοικειωθούν μαζί τους τα στρατεύματα. Επακόλουθο ήταν οι Γερμανοί και οι Αυστριακοί κρυπταναλυτές να μην έχουν ιδιαίτερες δυσκολίες να αποκρυπτογραφήσουν τα μηνύματά τους.[7]
Ο κώδικας του Καίσαρα μπορεί να βρεθεί σήμερα σε παιδικά παιχνίδια. Ένας κώδικας του Καίσαρα με μετατόπιση 13 χρησιμοποιείται από τον αλγόριθμο ROT13, μία απλή μέθοδο συσκότισης κειμένου που χρησιμοποιείται ευρέως στο Usenet για να συσκοτίζει το κείμενο (σε περιπτώσεις αστείων ή spoiler ιστοριών), αλλά δεν χρησιμοποιείται ως σοβαρή μέθοδος κρυπτογράφησης.[8]
Ο κώδικας Vigenère χρησιμοποιεί τον κώδικα του Καίσαρα με διαφορετική μετατόπιση σε κάθε θέση του κειμένου. Η τιμή της μετατόπισης καθορίζεται από την χρήση μιας επαναλαμβανόμενης λέξης κλειδί. Αν η λέξη κλειδί είναι τόσο μεγάλη όσο το μήνυμα, επιλεγμένη τυχαία, και δεν χρησιμοποιηθεί ποτέ ξανά, τότε ο κώδικας είναι σημειωματάριο μίας χρήσης, και έχει αποδειχτεί ότι δεν σπάει. Οι ιδανικές συνθήκες όμως είναι τόσο δύσκολο να ικανοποιηθούν που στην πράξη δεν γίνεται ποτέ. Λέξεις κλειδιά μικρότερες από το μήνυμα εισάγουν κυκλικό μοτίβο το οποίο μπορεί να εντοπιστεί με στατιστικώς προηγμένη εκδοχή της ανάλυσης συχνοτήτων.[9]
Τον Απρίλιο του 2006, ο φυγάς αρχηγός της μαφίας Μπερνάρντο Προβεζάνο συνελήφθη στη Σικελία, εν μέρει επειδή κάποια από τα μηνύματά του, γραμμένα σε παραλλαγή του κώδικα του Καίσαρα, αποκρυπτογραφήθηκαν. Ο κώδικας του Προβεζάνο έκανε χρήση αριθμών, έτσι ώστε το A γραφόταν ως 4, το B ως 5 και ούτω καθεξής.[10]
Το 2011, ο Ρατζίμπ Καρίμ καταδικάστηκε στο Ηνωμένο Βασίλειο για «αδικήματα τρομοκρατίας» αφού χρησιμοποίησε τον κώδικα του Καίσαρα για να επικοινωνήσει με ισλαμιστές ακτιβιστές από το Μπανγκλαντές, συζητώντας σχέδια για την ανατίναξη αεροπλάνων της British Airways ή την παρενόχληση των τηλεπικοινωνιακών της δικτύων. Παρόλο που και τα δύο μέρη είχαν πρόσβαση σε κατά πολύ καλύτερες τεχνικές κρυπτογράφησης (ο ίδιος ο Καρίμ χρησιμοποιούσε το PGP για αποθήκευση δεδομένων σε σκληρούς δίσκους), επέλεξαν να χρησιμοποιήσουν την δική τους μέθοδο (υλοποιημένη σε Microsoft Excel) «επειδή οι 'άπιστοι' το γνώριζαν [εν. το PGP] και έτσι ήταν λιγότερο ασφαλές».[11]
Σπάζοντας τον κώδικα
[Επεξεργασία | επεξεργασία κώδικα]| Μετατόπιση αποκρυπτογράφησης |
Υποψήφιο απλό κείμενο |
|---|---|
| 0 | exxegoexsrgi |
| 1 | dwwdfndwrqfh |
| 2 | cvvcemcvqpeg |
| 3 | buubdlbupodf |
| 4 | attackatonce |
| 5 | zsszbjzsnmbd |
| 6 | yrryaiyrmlac |
| ... | |
| 23 | haahjrhavujl |
| 24 | gzzgiqgzutik |
| 25 | fyyfhpfytshj |
Ο κώδικας του Καίσαρα μπορεί εύκολα να σπάσει ακόμα και με σενάριο κρυπτοκειμένου μόνο (ciphertext-only scenario). Μπορούν να ληφθούν υπόψη δύο περιπτώσεις
- ο επιτιθέμενος γνωρίζει (ή υποθέτει) ότι έχει χρησιμοποιηθεί κάποιου είδους κώδικας απλής αντικατάστασης, αλλά όχι ότι πρόκειται για τον κώδικα του Καίσαρα συγκεκριμένα.
- ο επιτιθέμενος γνωρίζει ότι πρόκειται για κώδικα του Καίσαρα, αλλά δεν γνωρίζει την τιμή της μετατόπισης.
Στην πρώτη περίπτωση ο κώδικας μπορεί να σπάσει χρησιμοποιώντας τις ίδιες τεχνικές όπως και σε ένα γενικό απλό κώδικα αντικατάστασης, όπως η ανάλυση συχνότητας ή οι λέξεις μοτίβα.[12] Ενώ θα λύνεται, είναι πιθανό ότι ο επιτιθέμενος θα διαπιστώσει σύντομα την κανονικότητα στη λύση και θα συμπεράνει ότι χρησιμοποιείται ο κώδικας του Καίσαρα.
Στη δεύτερη περίπτωση το σπάσιμο του κώδικα είναι ακόμα πιο εύκολο. Καθώς υπάρχει περιορισμένος μόνο αριθμός πιθανών μετακινήσεων (23 στα Ελληνικά), μπορούν να εξεταστούν με τη σειρά σε μία brute force attack.[13] Ένας τρόπος να γίνει αυτό είναι να γραφτεί ένα τμήμα του κρυπτογραφημένου κειμένου σε ένα πίνακα για όλες τις πιθανές μετατοπίσεις[14] - τεχνική που κάποιες φορές ονομάζεται «completing the plain component» (ολοκληρώνοντας το απλό συστατικό).[15] Το παράδειγμα που δίνεται είναι για το κρυπτογραφημένο κείμενο "EXXEGOEXSRGI", το κείμενο είναι αμέσως αναγνωρίσιμο με το μάτι στη μετατόπιση κατά 4.
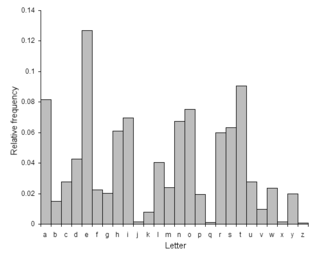
Μία άλλη προσέγγιση είναι η ταυτοποίηση των κατανομών συχνότητας των γραμμάτων. Σχεδιάζοντας τις συχνότητες των γραμμάτων στο κρυπτογραφημένο κείμενο, και γνωρίζοντας την αναμενόμενη κατανομή αυτών των γραμμάτων στην γλώσσα του κειμένο, ένας άνθρωπος μπορεί εύκολα να εντοπίσει την τιμή της μετατόπισης κοιτώντας την μετατόπιση συγκεκριμένων χαρακτηριστικών στο γράφημα. Αυτό είναι γνωστό ως ανάλυση συχνότητας. Για παράδειγμα στην αγγλική γλώσσα οι συχνότητες των γραμμάτων E, T (συνήθως τα πιο συχνά) και Q, Z (τυπικά τα λιγότερο συχνά) είναι ιδιαίτερα διακριτές.[16] Το ίδιο πράγμα μπορεί να γίνει και με υπολογιστή, μετρώντας το πόσο καλά η κατανομή συχνότητας ταιριάζει με την αναμενόμενη κατανομή.[17]
Για κείμενο φυσικής γλώσσας, θα υπάρχει, κατά πάσα πιθανότητα, μόνο μία αποκρυπτογράφηση, αν και για εξαιρετικά σύντομα κείμενα, μπορεί να υπάρχουν πολλαπλές λύσεις. Για παράδειγμα, το κρυπτογραφημένο κείμενο MPQY θα μπορούσε να αποκρυπτογραφηθεί είτε ως «aden» είτε ως «know» (αν υποτεθεί ότι το κείμενο είναι στα αγγλικά), ενώ κατά παρόμοιο τρόπο, το «ALIIP» μπορεί να είναι «dolls» ή «wheel» και το "AFCCP" να είναι «jolly» ή «cheer».
Πολλαπλές κρυπτογραφήσεις και αποκρυπτογραφήσεις δεν παρέχουν επιπρόσθετη ασφάλεια. Αυτό οφείλεται στο ότι δύο κρυπτογραφήσεις με μετατόπιση A και B θα είναι ισοδύναμες με μία κρυπτογράφησε με μετατόπιση A + B. Με μαθηματικούς όρους, η κρυπτογράφηση υπό διάφορα κλειδιά σχηματίζει μία ομάδα.[18]
Παραπομπές
[Επεξεργασία | επεξεργασία κώδικα]- ↑ Luciano, Dennis; Gordon Prichett (January 1987). «Cryptology: From Caesar Ciphers to Public-Key Cryptosystems». The College Mathematics Journal 18 (1): 2–17. doi:. https://archive.org/details/sim_college-mathematics-journal_1987-01_18_1/page/2.
- ↑ Wobst, Reinhard (2001). Cryptology Unlocked. Wiley. σελίδες 19. ISBN 978-0-470-06064-3.
- ↑ Reinke, Edgar C. (December 1992). «Classical Cryptography». The Classical Journal 58 (3): 114.
- ↑ Josef Pieprzyk· Thomas Hardjono· Jennifer Seberry (2003). Fundamentals of Computer Security. Springer. σελίδες 6. ISBN 3-540-43101-2.
- ↑ Singh, Simon (2000). The Code Book. Anchor. σελίδες 14–20. ISBN 0-385-49532-3.
- ↑ Kahn, David (1967). The Codebreakers. σελίδες 775–6. ISBN 978-0-684-83130-5.
- ↑ Kahn, David (1967). The Codebreakers. σελίδες 631–2. ISBN 978-0-684-83130-5.
- ↑ Wobst, Reinhard (2001). Cryptology Unlocked. Wiley. σελίδες 20. ISBN 978-0-470-06064-3.
- ↑ Kahn, David (1967). The Codebreakers. ISBN 978-0-684-83130-5.
- ↑ Leyden, John (2006-04-19). «Mafia boss undone by clumsy crypto». The Register. http://www.theregister.co.uk/2006/04/19/mafia_don_clueless_crypto/. Ανακτήθηκε στις 2008-06-13.
- ↑ «BA jihadist relied on Jesus-era encryption». The Register. 2011-03-22. http://www.theregister.co.uk/2011/03/22/ba_jihadist_trial_sentencing/. Ανακτήθηκε στις 2011-04-01.
- ↑ Beutelspacher, Albrecht (1994). Cryptology. Mathematical Association of America. σελίδες 9–11. ISBN 0-88385-504-6.
- ↑ Beutelspacher, Albrecht (1994). Cryptology. Mathematical Association of America. σελίδες 8–9. ISBN 0-88385-504-6.
- ↑ Leighton, Albert C. (April 1969). «Secret Communication among the Greeks and Romans». Technology and Culture 10 (2): 139–154. doi:. https://archive.org/details/sim_technology-and-culture_1969-04_10_2/page/139.
- ↑ Abraham Sinkov· Paul L. Irwin (1966). Elementary Cryptanalysis: A Mathematical Approach. Mathematical Association of America. σελίδες 13–15. ISBN 0-88385-622-0.
- ↑ Singh, Simon (2000). The Code Book. Anchor. σελίδες 72–77. ISBN 0-385-49532-3.
- ↑ Chris Savarese· Brian Hart (15 Ιουλίου 2002). «The Caesar Cipher». Αρχειοθετήθηκε από το πρωτότυπο στις 4 Ιουλίου 2008. Ανακτήθηκε στις 16 Ιουλίου 2008.
- ↑ Wobst, Reinhard (2001). Cryptology Unlocked. Wiley. σελίδες 31. ISBN 978-0-470-06064-3.



