Θεώρημα Ράμσεϋ

Στη συνδυαστική, το Θεώρημα Ράμσεϋ δηλώνει ότι σε οποιεσδήποτε χρωματισμένες κορυφές από ένα αρκετά μεγάλο πλήρες γράφημα, θα βρει κανείς μονοχρωματικό πλήρη υπογράφημα. Για δύο χρώματα, το θεώρημα Ramsey αναφέρει ότι για κάθε ζεύγος θετικών ακεραίων (r, s), υπάρχει ένας μικρότερος θετικός ακέραιος R (R, S) τέτοιος ώστε για κάθε 2-χρωματισμούς του πλήρες γράφημα R (r, s) κορυφές, υπάρχει ένα πλήρες μονοχρωματικό υπογράφημα είτε r ή s κορυφές. Εδώ R (R, S) σημαίνει έναν ακέραιο που εξαρτάται τόσο από r και s. Είναι κατανοητό να αντιπροσωπεύει το μικρότερο ακέραιο για την οποία το θεώρημα κατέχει.

Το θεώρημα του Ramsey είναι ένα θεμελιώδες αποτέλεσμα της Συνδυαστικής. Η πρώτη εκδοχή αυτού του αποτελέσματος αποδείχθηκε μέσω του F. P. Ramsey. Αυτό, ξεκίνησε τη συνδυαστική θεωρία που σήμερα ονομάζεται θεωρία ράμσεϋ,που επιδιώκει την κανονικότητα μέσα διαταραχή: γενικές προϋποθέσεις για την ύπαρξη υποδομών με τακτικές ιδιότητες. Σε αυτή την εφαρμογή είναι ένα ζήτημα της ύπαρξης μονοχρωματικά υποσύνολα, δηλαδή, υποσύνολα συνδεδεμένα άκρα του ένα μόνο χρώμα.

Η επέκταση αυτού του θεωρήματος ισχύει για κάθε πεπερασμένο αριθμό των χρωμάτων, και όχι μόνο για δύο. Ακριβέστερα, το θεώρημα δηλώνει ότι για οποιοδήποτε δεδομένο αριθμό χρωμάτων c, και οποιοδήποτε δεδομένο ακέραιοι n₁,...,n_c, υπάρχει ένας αριθμός, R(n₁, ..., n_c), έτσι ώστε όταν οι κορυφές ενός πλήρους γραφήματος R(n₁, ..., n_c) είναι χρωματισμένες με c διαφορετικά χρώματα, τότε για κάποιο i από 1 έως c,πρέπει να περιέχει ένα πλήρες υπογράφημα της τάξης n_i των οποίων οι κορυφές είναι όλες χρώμα i. Η ειδική περίπτωση παραπάνω έχει c = 2 (and n₁ = r and n₂ = s).

Παράδειγμα: R(3,3) = 6

A 2-χρωματισμός K₅ χωρίς μονοχρωματικό K₃

Στο ακόλουθο παράδειγμα, ο τύπος R(3,3) παρέχει μια λύση στο ζήτημα το οποίο ζητά από τον ελάχιστο αριθμό των κορυφών ενός γραφήματος πρέπει να περιέχει, προκειμένου να διασφαλιστεί ότι είτε (1) τουλάχιστον 3 κορυφές στο γράφημα που συνδέονται ή (2) τουλάχιστον 3 κορυφές στο γράφημα είναι ασύνδετες. Σημειώστε ότι, λόγω της συμμετρικής φύσεως του προβλήματος χώρου, R(r,s) είναι ίσο με R(s,r).

Ας υποθέσουμε ότι οι κορυφές ενός πλήρους γραφήματος 6 κορυφές χρώματος κόκκινο και μπλε. Διαλέγουμε μια κορυφή v. Υπάρχουν 5 κορυφές εκτός από τη v και έτσι (από αρχή περιστερώνα) τουλάχιστον 3 από αυτές θα πρέπει να είναι το ίδιο χρώμα. Χωρίς το πρόβλημα της γενικότητας μπορούμε να υποθέσουμε τουλάχιστον 3 από αυτές τις άκρες, που συνδέει την κορυφή v σε κορυφές r, s και t, είναι μπλε. (Αν όχι, η ανταλλαγή κόκκινο και μπλε σε ότι ακολουθεί.) Εάν κάποια από τις ακμές (R, S), (R, T), (s, t) είναι επίσης μπλε, τότε έχουμε ένα εντελώς μπλε τρίγωνο. Αν όχι, τότε αυτές οι τρεις πλευρές είναι όλα κόκκινα και έχουμε ένα εντελώς κόκκινο τρίγωνο. Δεδομένου ότι το επιχείρημα αυτό λειτουργεί για τις χρωστικές ουσίες, κάθε K6 περιέχει ένα μονοχρωματικό K3, και ως εκ τούτου, R (3,3) ≤ 6. Η δημοφιλής έκδοση αυτή ονομάζεται θεώρημα των φίλων και των αγνώστων.

Μια εναλλακτική απόδειξη λειτουργεί με διπλή μέτρηση. Στη συνέχεια, ως εξής: Μετρήστε τον αριθμό των διατεταγμένων τριπλών κορυφών x, y, z τέτοιο ώστε η άκρη (xy) να είναι κόκκινη και η ακμή (yz) είναι μπλε. Πρώτον, κάθε συγκεκριμένη κορυφή θα είναι η μέση είτε 0 × 5 = 0 (όλες οι ακμές από την κορυφή είναι το ίδιο χρώμα) 1 × 4 = 4 (τέσσερις έχουν το ίδιο χρώμα, το ένα είναι το άλλο χρώμα), ή 2 × 3 = 6 (τρεις έχουν το ίδιο χρώμα, δύο είναι το άλλο χρώμα), όπως τρίκλινα. Ως εκ τούτου, υπάρχουν πλέον 6 × 6 = 36 τέτοιες τριάδες. Δεύτερον, για κάθε μη-μονοχρωματικό τρίγωνο (xyz), υπάρχουν ακριβώς δύο τέτοιες τριάδες. Ως εκ τούτου, υπάρχουν πλέον 18 μη μονοχρωματικά τρίγωνα. Ως εκ τούτου, τουλάχιστον 2 από τα 20 τρίγωνα στο Κ6 είναι μονοχρωματικά.

Αντίθετα, είναι δυνατόν να 2-χρώμα ένα Κ5 χωρίς να δημιουργεί μονοχρωματικό K3, δείχνοντας ότι η R (3,3)> 5. Το μοναδικό χρώμα εμφανίζεται στα δεξιά. έτσι R(3,3) = 6.

Το έργο της απόδειξης ότι η R(3,3) ≤ 6 ήταν ένα από τα προβλήματα των William Lowell Putnam Mathematical Competition το 1953.

Απόδειξη του θεωρήματος

2-υπόθεση χρώμα

Αρχικά θα αποδείξουμε το θεώρημα για την περίπτωση 2-χρώμα, με μαθηματική επαγωγή για r + s. Είναι σαφές από τον ορισμό ότι για όλα τα n, R(n, 1) = R(1, n) = 1. Αυτό ξεκινά την επαγωγή. Έχουμε αποδείξει ότι το R(r, s) υπάρχει με την εύρεση μιας ρητής που δεσμεύεται γι 'αυτό. Από την επαγωγική υπόθεση R(r − 1, s) και R(r, s − 1) υπάρχει.

Λήμμα 1. R(r, s) ≤ R(r − 1, s) + R(r, s − 1):

Απόδειξη.Σκεφτείτε ένα πλήρες γράφημα για R(r − 1, s) + R(r, s − 1) κορυφές των οποίων οι ακμές είναι χρωματισμένες με δύο χρώματα. Διαλέξτε μια κορυφή v από τη γραφική παράσταση, και κατανείμετε τις υπόλοιπες κορυφές σε δύο σύνολα M και N,τέτοια ώστε για κάθε κορυφή w, το w ανήκει στο M αν (v, w) είναι μπλε, και w ανήκει στο N αν (v, w) είναι κόκκινο.Επειδή η γραφική παράσταση έχει R(r − 1, s) + R(r, s − 1) = |M| + |N| + 1 κορυφές, συνάγεται ότι είτε |M| ≥ R(r − 1, s) είτε |N| ≥ R(r, s − 1). Στην πρώτη περίπτωση, αν το Μ έχει ένα κόκκινο K_s στη συνέχεια το ίδιο κάνει και το αρχικό γράφημα και τελειώσαμε.Αλλιώς το M έχει ένα μπλε K_r−1 και έτσι το M ∪ {v} έχει μπλε K_r εξ ορισμού από το M.Η τελευταία περίπτωση είναι ανάλογη. Έτσι, ο ισχυρισμός είναι αληθής και έχουμε ολοκληρώσει την απόδειξη για τα 2 χρώματα.

Σημείωση.Στην περίπτωση 2 χρωμάτων, αν R(r − 1, s) και R(r, s − 1) είναι και οι δύο άρτιοι , η ανισότητα επαγωγής μπορεί να ενισχυθεί για να:

R(r, s) ≤ R(r − 1, s) + R(r, s − 1) − 1.

Γενική περίπτωση

Αποδεικνύουμε τώρα το αποτέλεσμα για τη γενική περίπτωση της με c χρώματα. Η απόδειξη είναι και πάλι από την επαγωγή, αυτή τη φορά σχετικά με τον αριθμό των χρωμάτων c. Έχουμε το αποτέλεσμα για c = 1 και c = 2 (ανωτέρω). Τώρα ας c> 2.

Λήμμα 2. R(n₁, ..., n_c) ≤ R(n₁, ..., n_c−2, R(n_c−1, n_c)).

Απόδειξη.Σκεφτείτε ένα γράφημα για t κορυφές και χρωματίζουν τις άκρες του με c χρώματα.Τώρα «πάμε αχρωματοψία» και υποθέτουμε ότι c − 1 και c έχουν το ίδιο χρώμα. Έτσι, η γραφική παράσταση είναι τώρα (c − 1)-χρωματισμένη.Από την επαγωγική υπόθεση, που περιέχει είτε ένα K_ni μονοχρωματικά με το χρώμα i για κάποια 1 ≤ i ≤ c − 2 ή ένα K_R(nc−1,nc)-χρωματισμένο με «θολό χρώμα». Στην πρώτη περίπτωση έχουμε τελειώσει. Στην τελευταία περίπτωση, μπορούμε να ανακτήσουμε πάλι την όραση μας και να δούμε από τον ορισμό ότι για R(n_c−1, n_c) εμείς πρέπει να έχουμε είτε μια (c − 1)-μονόχρωμη K_nc−1 είτε μια c-μονόχρωμη K_nc. Σε κάθε περίπτωση η απόδειξη είναι πλήρης.

Η δεξιά πλευρά της ανισότητας στο λήμμα 2 περιέχει Ramsey αριθμούς για c − 1 χρώματα και 2 χρώματα, και ως εκ τούτου υπάρχει και είναι ένας πεπερασμένος αριθμός t,από την επαγωγική υπόθεση. Έτσι, αποδεικνύοντας τον ισχυρισμό θα αποδειχθεί το θεώρημα.

Αριθμοί Ράμσεϋ

Οι αριθμοί R(r,s) στο θεώρημα Ramseym (και οι επεκτάσεις τους σε περισσότερα από δύο χρώματα) είναι γνωστά ως Αριθμοί Ramsey. Ένα άνω φράγμα για το R(r,s) μπορεί να εξαχθεί από την απόδειξη του θεωρήματος, και άλλα επιχειρήματα δίνουν χαμηλότερα όρια.(Το πρώτο κάτω φράγμα εφευρέθηκε από τον Paul Erdős χρησιμοποιώντας την πιθανολογική μέθοδος.)Ωστόσο, υπάρχει ένα τεράστιο χάσμα μεταξύ των πιο στενών χαμηλότερα ορίων και των πιο στενών άνω φραγμάτων. Ως εκ τούτου, υπάρχουν πολύ λίγοι αριθμοί r και s για το οποίο γνωρίζουμε την ακριβή τιμή του R(r,s). Υπολογίζοντας ένα κάτω φράγμα L για το R(r,s) απαιτεί συνήθως εμφάνιση μπλε / κόκκινο χρωματισμό του γραφήματος K_L−1 με καθόλου μπλε K_r υπογράφημα και καθόλου κόκκινο K_s υπογράφημα.Τα άνω όρια αυτά είναι συχνά πολύ πιο δύσκολο να προσδιοριστούν: ένα είτε πρέπει να ελέγξει όλους τους πιθανούς χρωματισμούς προκειμένου να επιβεβαιωθεί η απουσία του αντιπαραδείγματος, ή να παρουσιάσει ένα μαθηματικό επιχείρημα για την απουσία του. Ένα εξελιγμένο πρόγραμμα υπολογιστή δεν χρειάζεται να εξετάσει όλες τις χρωστικές ουσίες ξεχωριστά, προκειμένου να εξαλειφθούν όλα αυτά ; παρ 'όλα αυτά είναι ένα πολύ δύσκολο υπολογιστικό έργο για το υπάρχον λογισμικό που μπορεί να διαχειριστεί μόνο μικρά μεγέθη.

Η πολυπλοκότητα για την αναζήτηση όλων των πιθανών γραφημάτων (via ωμής βίας) είναι O(2^{(n−1)(n−2)/2})για ένα άνω όριο n κόμβων .

Όπως περιγράφεται παραπάνω, R(3,3) = 6. Είναι πολύ εύκολο να αποδείξουμε ότι R R(4,2) = 4, και, γενικότερα, ότι R(s,2) = s για κάθε s: ένα γράφημα για s − 1 κόμβους με όλα τα άκρα χρωματισμένα κόκκινα χρησιμεύει ως αντιπαράδειγμα και αποδεικνύει ότι R(s,2) ≥ s ; s μεταξύ χρωματισμούς ενός γραφήματος s κόμβων, ο χρωματισμός με όλα τα άκρα χρωματισμένα κόκκινα περιέχει ένα s-κόμβο κόκκινο υπογράφημα, και όλες οι άλλες χρωστικές ουσίες περιέχουν ένα 2-κόμβο μπλε υπογράφημα (δηλαδή, ένα ζεύγος κόμβων που συνδέονται με μπλε άκρη) Χρησιμοποιώντας τις ανισότητες επαγωγής, μπορεί να συναχθεί το συμπέρασμα ότι R(4,3) ≤ R(4,2) + R(3,3) − 1 = 9, και ως εκ τούτου R(4,4) ≤ R(4,3) + R(3,4) ≤ 18. Υπάρχουν δύο (4,4,16) γραφήματα (τα οποία είναι, 2-χρωστικές ενός πλήρους γραφήματος σε 16 κόμβους χωρίς 4-κόμβο κόκκινο η μπλε πλήρη υπογραφημάτων ) μεταξύ 6.4×10²² διαφορετικών 2-χρωστικών για 16-κόμβους γραφημάτων, και μόνο ένα (4,4,17) γραφήματα (το Paley graph τάξης 17) μεταξύ 2.46×10²⁶ χρωστικών. (Αυτό αποδείχτηκε από τους Evans, Pulham και Sheehan το 1979.) . Έπεται ότιR(4,4) = 18.

Το γεγονός ότι R(4,5)=25 καθιερώθηκε για πρώτη φορά από τους Brendan McKay και Stanisław Radziszowski το 1995.

Η ακριβής τιμή του R(5,5) είναι άγνωστη, αν και είναι γνωστό ότι είναι μεταξύ του 43 (Geoffrey Exoo) και του 49 (McKay and Radziszowski)

« Erdős ζητά από μας να φανταστούμε μια εξωγήινη δύναμη, πολύ πιο ισχυρή από ό,τι εμείς, που προσγειώνεται στη Γη και ζητάει την τιμή του R (5,5) ή θα καταστρέψει τον πλανήτη μας. Στην περίπτωση αυτή, ισχυρίζεται ότι θα πρέπει να συγκεντρώσουν όλους τους υπολογιστές μας και όλοι μαθηματικοί μας και να προσπαθήσει να βρει την τιμή. Αλλά ας υποθέσουμε, αντίθετα, ότι ζητούν R(6,6). Στην περίπτωση αυτή, ο ίδιος πιστεύει ότι θα πρέπει να προσπαθήσει να καταστρέψει τους εξωγήινους. » — Joel Spencer

Οι McKay, Radziszowski και Exoo μέθοδοι που χρησιμοποιούνται για την δημιουργία γραφημάτων με τη βοήθεια υπολογιστή σε εικασίες το 1997 όπου R(5,5) είναι ακριβώς 43. Ήταν σε θέση να κατασκευάσουν ακριβώς 656 (5,5,42) γραφήματα, φθάνουν στο ίδιο σύνολο γραφημάτων μέσω διαφορετικών οδών. Κανένα από τα 656 γραφήματα δεν μπορεί να επεκταθεί σε ένα (5,5,43) γράφημα.

Για R(r,s) με r, s > 5, μόνο αδύναμα όρια είναι διαθέσιμα. Κάτω όρια για R(6,6) και R(8,8) δεν έχουν βελτιωθεί από το 1965 και το 1972, αντίστοιχα.

R(r,s) για τιμές των r και s μεγαλύτερες του 10 δίνονται στον παρακάτω πίνακα.  Όπου η ακριβής τιμή είναι άγνωστη ο πίνακας μας δίνει τα καλύτερα γνωστά όρια.R(r,s) για τιμές των r και s μικρότερες από 3 δίνονται από τα R(1,s) = 1 και R(2,s) = s για κάθε τιμή του s. Η τυπική έρευνα για την ανάπτυξη της έρευνας Ramsey-αριθμός έχει γραφτεί από τον Stanisław Radziszowski.

r,s	1	2	3	4	5	6	7	8	9	10
1	1
2	1	2
3	1	3	6
4	1	4	9	18
5	1	5	14	25	43–49
6	1	6	18	36–41	58–87	102–165
7	1	7	23	49–61	80–143	113–298	205–540
8	1	8	28	58–84	101–216	132–495	217–1031	282–1870
9	1	9	36	73–115	126–316	169–780	241–1713	317–3583	565–6588
10	1	10	40–42	92–149	144–442	179–1171	289–2826	331–6090	581–12677	798–23556

Από τότε που R(r, s) = R(s, r), υπάρχει μια ασήμαντη συμμετρία σε όλη τη διαγώνιο.

Αυτός ο πίνακας είναι απόσπασμα από ένα μεγαλύτερο πίνακα που είχε συλλεχθεί από τον Stanisław Radziszowski.

Ασύμπτωτες

Η ανισότητα R(r, s) ≤ R(r − 1, s) + R(r, s − 1) εφαρμόζεται επαγωγικά και αποδεικνύεται οτι:

$R(r,s)\leq {\binom {r+s-2}{r-1}}.$

Συγκεκριμένα, αυτό το αποτέλεσμα, χάρης στους Erdős και Szekeres, μας δείχνει ότι όταν r = s,

$R(s,s)\leq (1+o(1)){\frac {4^{s-1}}{\sqrt {\pi s}}}.$

Ένα εκθετικό κάτω φράγμα,

$R(s,s)\geq (1+o(1)){\frac {s}{{\sqrt {2}}e}}2^{\frac {s}{2}},$

δόθηκε από τον Erdős το 1947 and και ήταν καθοριστικό για την πιθανό θεωρητική του προσέγγιση. Προφανώς υπάρχει μεγάλη διαφορά μεταξύ των δύο φραγμάτων: για παράδειγμα, για s = 10, έχουμε 101 ≤ R(10,10) ≤ 48620. Γενικά, οι παράγοντες της εκθετικής αύξησης κάθε φράγματος δεν έχουν βελτιωθεί μέχρι σήμερα και ακόμα σταθεροποιούνται ανάμεσα στο 4 και ${\sqrt {2}}$ αντίστοιχα. Δεν υπάρχει κάποιος ενδεδειγμένος τρόπος κατασκευής χαμηλότερου εκθετικού κάτω φράγματος. Τα πιο γνωστά άνω και κάτω φράγματα για διαγώνιους αριθμούς Ράμσευ αυτή τη στιγμή είναι:

$(1+o(1)){\frac {{\sqrt {2}}s}{e}}2^{\frac {s}{2}}\leq R(s,s)\leq s^{-{\frac {c\log s}{\log \log s}}}4^{s},$

Χάρις στους Spencer και Conlon αντίστοιχα.

Για τους εκτός-διαγωνίου αριθμους Ράμσευ-R(3,t), είναι γνωστό ότι είναι της τάξης ${\tfrac {t^{2}}{\log t}}$; αυτό μπορεί να εκφραστεί διαφορετικά, λέγοντας οτι ο μικρότερος πιθανός "ανεξάρτητος αριθμός" (independence number) σε ένα n-vertex ελεύθερο-τριγώνου γράφημα (tτριγώνου-ελεύθερο γράφημα) είναι $\Theta ({\sqrt {n\log n}})$. Το άνω φράγμα για R(3,t) δίνεται από τους Ajtai, Komlós, και Szemerédi, και το κάτω Kim. Γενικότερα για τους εκτός διαγωνίου αριθμους Ramsey R(s, t) με s επιλεγμένο και t αυξανόμενο, τα φράγματα με τη καλύτερη προσέγγιση είναι:

$c'_{s}{\frac {t^{\frac {s+1}{2}}}{(\log t)^{{\frac {s+1}{2}}-{\frac {1}{s-2}}}}}\leq R(s,t)\leq c_{s}{\frac {t^{s-1}}{(\log t)^{s-2}}},$

χάρις στους Bohman και Keevash και Ajtai, Komlós και Szemerédi αντίστοιχα.

Ένα πολύχρωμο παράδειγμα: R(3,3,3) = 17

Οι μόνες δύο 3-χρωστικές ουσίες K₁₆ χωρίς μονοχρωματικό K₃.

Ένας πολύχρωμος αριθμός Ράμσευ είναι ένας αριθμός Ράμσευ με 3 ή περισσότερα χρώματα. Υπάρχει μόνο ένας τετριμμένος πολύχρωμος αριθμός Ράμσευ για τον οποίο η ακριβής τιμή του είναι γνωστή, ο R(3,3,3) = 17.

Έστω ότι έχουμε την γωνία ενός πλήρους γραφήματος χρωματισμένη με τρία χρώματα, κόκκινο, κίτρινο και πράσινο. Έστω ακόμη ότι πως αυτή η άκρη του φραφήματος δεν έχει μονοχρωματικά τρίγωνα. Επιλέγουμε ενα ακρότατο v. Θεωρούμε το σύνολο των ακροτάτων τα οποία έχουν πράσινη πλευρά στο ακρότατο ν. Αυτό ονομάζεται "πράσινη γειτονιά του ν". Η πράσινη γειτονιά του ν δεν μπορεί να περιέχει άλλες πράσινες πλευρές, αφού αν είχε θα υπήρχαν τρίγωνα με τρεις πράσινες γωνίες στα δύο καταληκτικά σημεία αυτής της πράσινης γειτονιάς και του ακροτάτου ν. Συνεπώς, η περιεχόμενη γωνία χρωματιζόμενη στη πρασινη γειτονιά του ν έχει πλευρές χρωματιζόμενες μόνο με 2 χρώματα, το κίτρινο και το κόκκινο. Αφού R(3,3) = 6, η πράσινη γειτονιά του ν μπορει να περιέχει 5 ακρότατα. Ομοίως, οι κόκκινες και πράσινες γειτονιές του ν μπορούν να περιέχουν το πολυ 5 ακρότατα η κάθε μιαred and yellow. Αφού κάθε ακρότατο , εκτός από το ίδιο το ν ,είναι σε μία από τις πράσινες ,κόκκινες ή κίτρινες γειτονιές του ν, όλο το πλήρες γράφημα μπορεί να έχει 1 + 5 + 5 + 5 = 16 ακρότατα. Άρα, έχουμε R(3,3,3) ≤ 17.

Για να δούμε οτι το R(3,3,3) ≥ 17, επαρκεί για να ισοσταθμήσουμε μία γωνία χρωματίζοντας στην στο πλήρες γράφημα σε 16 ακρότατα με 3 χρώματα για να αποφύγουμε τα μονοχρωματικά τρίγωνα. Φαίνεται ότι υπάρχουν μόνο δύο χρωματισμοί στον K₁₆, οι αποκαλλούμενοι στρεβλοί και μη-στρεβλοί. Και οι δύο φαίνονται στο σχήμα στα δεξιά της σελίδας, με τον στρεβλό στο πάνω μέρος και τον μη-στρεβλό στο κάτω.Και στους δύο χρωματισμούς, παρατηρήστε οτι τα ακρότατα έχουν επισημανθεί, και οτι απο το v₁₁ εως το v₁₅ έχουν σκιαγραφηθεί διπλά,και στα αριστερά και στα δεξία ,για να απλοποιήσουμε.

Συνεπώς, R(3,3,3) = 17.

Clebsch graph

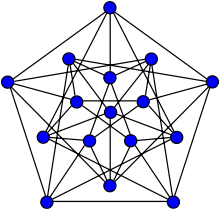
Αν επιλέξουμε ένα χρώμα σε οποιοδήποτε στρεβλό ή μη στρεβλό γράφημα K₁₆, και θεωρήσουμε το γράφημα του οποίου οι γωνίες είναι ακριβώς αυτές με το συγκεκριμμένο χρώμα, τότε θα έχουμε ένα διάγραμμα Clebsch (Clebsch γράφημα).

Είναι γνωστό ότι υπάρχουν 3 χρωματισμοί με 3 χρώματα στον K₁₅ οι οποίοι αποφεύγουν τα μονοχρωματικά τρίγωνα, και μπορούν να κατασκευαστούν σβήνοντας οποιοδήποτε ακρότατο απο το στρεβλό και μη στρεβλό διάγραμμα του K₁₆, διαδοχικά.

Είναι επίσης γνωστό ότι υπάρχουν 115 χρωματισμοί γωνιών με 3 χρώματα στον K₁₄ που αποφεύγουν τα μονοχρωματικά τρίγωνα,δεδομένου ότι θεωρουμε τους χρωματισμούς των γωνιών που διαφέρουν κατά μία μετάθεση χρώματος από το να γίνουν οι ίδιο.

Επεκτάσεις του θεωρήματος

Το θεώρημα μπορεί επίσης να επεκταθεί σε υπεργραφήματα. Ένα m-υπερ-γράφος είναι μια γραφική παράσταση του οποίου "άκρες" είναι σύνολα κορυφών m - σε ένα κανονικό γράφημα και μια ακμή είναι ένα σύνολο από 2 κορυφές. Η πλήρης δήλωση του θεωρήματος του Ramsey για υπεργραφήματα είναι ότι για κάθε ακέραιους m και c, και κάθε ακέραιοι n₁,...,n_c,υπάρχει ένας ακέραιος R(n₁, ..., n_c;c,m) οπότε, αν οι hyperedges ενός πλήρους m-υπεργράφημα της τάξης R(n₁,...,n_c;c,m), χρωματισμένα με διαφορετικά χρώματα C, τότε για κάποια i μεταξύ 1 και c, η υπεργράφημα πρέπει να περιλαμβάνει μια πλήρη υπο-m-υπεργράφημα της ni τάξη που hyperedges είναι όλα τα χρώματα i. Το θεώρημα αυτό συνήθως αποδεικνύεται από επαγωγή στο m, το «υπερ-ness» του γραφήματος. Η βασική περίπτωση για την απόδειξη είναι m = 2, το οποίο είναι ακριβώς το παραπάνω θεώρημα.

Απειροστικό θεώρημα Ramsey

Ένα περαιτέρω αποτέλεσμα, επίσης κοινώς ονομάζεται θεώρημα Ράμσεϊ, εφαρμόζεται σε άπειρες γραφικές παραστάσεις. Σε ένα πλαίσιο όπου πεπερασμένα γραφήματα συζητούνται επίσης είναι συχνά αποκαλείται το «Άπειρο Ramsey θεώρημα".Διαισθητικά όπως παρέχονται από την εικονογραφημένη αναπαράσταση ενός γραφήματος είναι μειωμένη κατά τη μετακίνηση από το πεπερασμένο στο άπειρο γραφήματα, θεωρήματα σε αυτόν τον τομέα είναι συνήθως διατυπώνονται σε σύνολο-θεωρητικές ορολογία.

Θεώρημα. Έστω X κάποιο αριθμήσιμο άπειρο σύνολο και το χρώμα των στοιχείων του X⁽ⁿ⁾ (υποσύνολα του X μεγέθους n) σε c διαφορετικά χρώματα. Τότε υπάρχει κάποιο άπειρο υποσύνολο M του X τέτοιο ώστε με μέγεθος n υποσυνόλων M όλα έχουν το ίδιο χρώμα.

Απόδειξη :Η απόδειξη δίνεται για c = 2 Είναι εύκολο να αποδείξει το θεώρημα για έναν αυθαίρετο αριθμό χρωμάτων χρησιμοποιώντας το επιχείρημα «αχρωματοψία», όπως παραπάνω.. Η απόδειξη γίνεται με (πλήρης) επαγωγή στο n, το μέγεθος των υποσυνόλων. Για n = 1, η δήλωση είναι ισοδύναμη με λέγοντας ότι αν χωρίσετε ένα άπειρο σύνολο σε δύο ομάδες, μία από αυτές είναι άπειρη. Αυτό είναι εμφανές. Υποθέτοντας ότι το θεώρημα ισχύει για n ≤ r, θα το αποδείξουμε για n = r + 1. Λαμβάνοντας υπόψη ένα 2-χρωματισμός των υποσυνόλων (r + 1)-στοιχείο του Χ, ας a₀ είναι ένα στοιχείο του Χ και αφήστε Υ = Χ \ {a₀}. Στη συνέχεια, να προκαλέσει μια 2-χρωματισμός των υποσυνόλων r-στοιχείο του Y, προσθέτοντας απλά a₀ σε κάθε υποσύνολο r-στοιχείου (για να πάρετε μια (r + 1)-υποσύνολο στοιχείο του Χ). Από την επαγωγική υπόθεση, υπάρχει ένας άπειρος Y₁ υποσύνολο εντός Y τέτοια ώστε κάθε στοιχείο r-υποσύνολο των Y₁ είναι χρωματισμένο το ίδιο χρώμα στην επαγόμενη χρωματισμό. Έτσι, υπάρχει μια a₀ στοιχείο και ένα άπειρο υποσύνολο Y₁ τέτοια ώστε όλη η (r + 1)-στοιχείου υποσύνολα του Χ που αποτελείται από a₀ και r στοιχεία των Y₁ έχουν το ίδιο χρώμα. Από το ίδιο επιχείρημα, υπάρχει ένα στοιχείο στο Y₁ και ένα άπειρο υποσύνολο των Y₁ Y₂ με τις ίδιες ιδιότητες. Επαγωγικά, παίρνουμε μια ακολουθία {a₀, a₁, a₂, ...} τέτοια ώστε το χρώμα του κάθε (r + 1)-υποσύνολο στοιχείο (a_i(1),(a_i(2)), ..., (a_i(r + 1)) με το i i(1) < i(2)<... <i(r + 1) εξαρτάται μόνο από την τιμή του i(1). Περαιτέρω, υπάρχουν άπειρες τιμές του i(1) έτσι ώστε αυτό το χρώμα θα είναι το ίδιο. Πάρτε αυτά τα a_i(n) να πάρει το επιθυμητό μονοχρωματικό σύνολο.

Η άπειρη προϋποθέτει την πεπερασμένη

Είναι δυνατόν να συναχθεί το πεπερασμένο θεώρημα Ramsey από την έκδοση του άπειρου, από την απόδειξη με αντίφαση.Ας υποθέσουμε ότι το πεπερασμένο θεώρημα Ramsey είναι ψευδή. Τότε υπάρχουν ακέραιοι c, n, T τέτοιοι ώστε για κάθε ακέραιο k, υπάρχει ένας c-χρωματισμός $[k]^{(n)}$ χωρίς ένα μονοχρωματικό σύνολο μεγέθους T.Ας C_k δηλώνουν τις c-χρωστικές ουσίες $[k]^{(n)}$ χωρίς ένα μονοχρωματικό σύνολο μεγέθους T.

Για κάθε k, ο περιορισμός μιας χρωστικής από C_k+1 σε $[k]^{(n)}$ (αγνοώντας το χρώμα όλων των συνόλων που περιέχουν k+1) είναι ένας χρωματισμός σε C_k.Ορίζουν $C_{k}^{1}$ να είναι οι χρωστικές ουσίες σε C_k οι οποίες είναι οι περιορισμοί των χρωστικών ουσιών στα C_k+1. Όσο C_k+1 δεν είναι κενή, ούτε είναι $C_{k}^{1}$.

Ομοίως, ο περιορισμός για τις χρωστικές ουσίες σε $C_{k+1}^{1}$ είναι σε $C_{k}^{1}$, επιτρέποντας έτσι να καθορίσει $C_{k}^{2}$ ως το σύνολο όλων αυτών των περιορισμών, ένα μη-κενό σύνολο. Συνεχίζοντας έτσι, ορίζουν $C_{k}^{m}$ για όλους τους ακέραιους m, k.

Τώρα, για κάθε ακέραιο k, $C_{k}\supseteq C_{k}^{1}\supseteq C_{k}^{2}\supseteq \dots$,και κάθε σύνολο, είναι μη κενό. Επιπλέον, C_k είναι πεπερασμένη, όπως $|C_{k}|\leq c^{\frac {k!}{n!(k-n)!}}$. Επομένως, η διασταύρωση όλων αυτών των συνόλων είναι μη κενή, και ας $D_{k}=C_{k}\cap C_{k}^{1}\cap C_{k}^{2}\cap \dots$.Στη συνέχεια, κάθε χρωματισμός σε D_k είναι ο περιορισμός μιας χρωστικής σε D_k+1.Ως εκ τούτου, με την unrestricting χρωστική σε D_k σε χρωστικές ουσίες D_k+1, και συνεχίζοντας αυτόν τον τρόπο, ένας κατασκευάζει ένα χρωματισμό $\mathbb {N} ^{(n)}$ χωρίς μονοχρωματικό σύνολο μεγέθους T. Αυτό έρχεται σε αντίθεση με το άπειρο θεώρημα Ramsey.

Αν μια κατάλληλη τοπολογική άποψη έχει ληφθεί, το επιχείρημα αυτό μετατρέπεται σε ένα τυπικό συμπαγές επιχείρημα δείχνοντας ότι η άπειρη έκδοση του θεωρήματος συνεπάγεται την πεπερασμένη έκδοση.

Κατευθυνόμενο γράφημα αριθμοί Ramsey

Είναι επίσης δυνατό να καθοριστούν οι αριθμοί Ramsey για κατευθυνόμενη γραφήματα. (Αυτά εισήχθησαν από P. Erdős & L. Moser.) Έστω R (n) είναι ο μικρότερος αριθμός Q τέτοιος ώστε κάθε πλήρες γράφημα με μεμονωμένα τόξα (ονομάζεται επίσης «τουρνουά») και με κόμβους ≥ Q περιέχει μία μη κυκλική (ονομάζεται επίσης "μεταβατικό") τουρνουά υπο n-κόμβο.

Αυτό είναι το ανάλογο κατευθυνόμενο γράφημα του τι (ανωτέρω) έχει κληθεί R (Ν, Ν? 2), ο μικρότερος αριθμός Ζ τέτοια ώστε κάθε 2-χρωματισμός των ακμών ενός πλήρους μη-κατευθυνόμενου γραφήματος με ≥ Ζ κόμβους, περιέχει ένα μονοχρωματικό πλήρες γράφημα n κόμβων. (Η κατευθυνόμενη αναλογική των δύο πιθανών χρώματα τόξου είναι οι δύο κατευθύνσεις των τόξων, το ανάλογο της «μονοχρωματικό" είναι "όλα τα arc-βέλη δείχνουν τον ίδιο τρόπο", δηλαδή "άκυκλων.")

Πράγματι, πολλοί που θεωρούν το κατευθυνόμενο γράφημα για να είναι πιο κομψό από το μη-κατευθυνόμενο. Έχουμε R(0) = 0, το R(1) = 1, το R(2) = 2, το R(3) = 4, το R(4) = 8, το R(5) = 14, το R(6) = 28 , 32 ≤ R(7) ≤ 55, και R(8) είναι ένα πρόβλημα και πάλι, σύμφωνα με Erdős, ότι κάποιος δεν θέλει ισχυρό αλλοδαπούς να θέσουν.

Αναφορές

• Ajtai, Miklós; Komlós, János; Szemerédi, Endre (1980), «A note on Ramsey numbers», J. Combin. Theory Ser. A 29 (3): 354–360, doi:10.1016/0097-3165(80)90030-8 .
• Bohman, Tom; Keevash, Peter (2010), «The early evolution of the H-free process», Invent. Math. 181 (2): 291–336, doi:10.1007/s00222-010-0247-x .
• Conlon, D. (2009), «A new upper bound for diagonal Ramsey numbers», Annals of Mathematics 170 (2): 941–960, doi:10.4007/annals.2009.170.941 .
• Do, Norman (2006). «Party problems and Ramsey theory». Austr. Math. Soc. Gazette 33 (5): 306-312. http://www.austms.org.au/Publ/Gazette/2006/Nov06/Nov06.pdf#page=48. 
• Erdős, Paul (1947), «Some remarks on the theory of graphs», Bull. Amer. Math. Soc. 53 (4): 292–294, doi:10.1090/S0002-9904-1947-08785-1 .
• Erdős, Paul; Szekeres, George (1935), «A combinatorial problem in geometry», Compositio Mathematica 2: 463–470, doi:10.1007/978-0-8176-4842-8_3, ISBN 978-0-8176-4841-1 .
• Exoo, G. (1989), «A lower bound for R(5,5)», Journal of Graph Theory 13: 97–98, doi:10.1002/jgt.3190130113 .
• Graham, R.; Rothschild, B.; Spencer, J. H. (1990), Ramsey Theory, New York: John Wiley and Sons .
• Ramsey, F. P. (1930), «On a problem of formal logic», Proceedings of the London Mathematical Society 30: 264–286, doi:10.1112/plms/s2-30.1.264 .
• Spencer, J. (1975), «Ramsey's theorem – a new lower bound», J. Combin. Theory Ser. A 18: 108–115, doi:10.1016/0097-3165(75)90071-0 .
• Bian, Zhengbing; Chudak, Fabian; Macready, William G.; Clark, Lane; Gaitan, Frank (2013), «Experimental determination of Ramsey numbers», Physical Review Letters 111: 130505-1 - 130505-6, doi:10.1103/PhysRevLett.111.130505 .

Δείτε επίσης

• Hazewinkel, Michiel, επιμ.. (2001), «Ramsey theorem», Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, http://www.encyclopediaofmath.org/index.php?title=p/r077240 
• Ramsey@Home είναι ένα distributed computing έργο που έχει σχεδιαστεί για να βρει νέα χαμηλότερα όρια για διάφορους αριθμούς Ramsey, χρησιμοποιώντας μια σειρά από διαφορετικές τεχνικές.
• Radziszowski's survey of small Ramsey numbers
• αυτός ο lisp code υπολογίζει άνω φράγματα για συγκεκριμένα νούμερα Ramsey δοθεί οι γενικοί κανόνες Radziszowski
• Survey of directed-graph Ramsey numbers
• Ramsey Number – from MathWorld (περιέχει κάτω και άνω όρια μέχρι R(19,19))
• Ramsey Number – Geoffrey Exoo (περιέχει R(5,5) > 42 αντι-απόδειξη)