Σύνδεση affine

Μια σύνδεση affine στη σφαίρα κυλά το affine εφαπτόμενο επίπεδο από το ένα σημείο στο άλλο. Καθώς το κάνει αυτό, το σημείο επαφής διαγράφει μια καμπύλη στο επίπεδο: το "ανάπτυγμα".

Στον κλάδο των ̼μαθηματικών̺ που ονομάζεται διαφορική γεωμετρία, μια σύνδεση affine είναι ένα γεωμετρικό αντικείμενο σε μια ομαλή πολλαπλή που συνδέει κοντινά διαστήματα εφαπτομένης, και έτσι επιτρέπει εφαπτόμενα διανυσματικά πεδία να διαφοροποιούνται σαν να ήταν λειτουργίες στην πολλαπλή με τιμές σε ένα σταθερό χώρο φορέα. Η έννοια της affine σύνδεσης έχει τις ρίζες του στη γεωμετρία του 19ου αιώνα και ο τανυστής λογισμός, αλλά δεν είχε αναπτυχθεί πλήρως μέχρι τις αρχές της δεκαετίας του 1920, από τον Élie Cartan (ως μέρος της γενικής θεωρίας του για τις συνδέσεις) και Hermann Weyl (που χρησιμοποιείται για την έννοια ως ένα μέρος των θεμελίων του για τη γενική σχετικότητα). Η ορολογία που οφείλεται σε Cartan και έχει τις ρίζες της στον εντοπισμό των χώρων εφαπτομένης στoν Ευκλείδειο χώρο R^n από μετάφραση: η ιδέα είναι ότι η επιλογή των affine σύνδεση κάνει μια πολλαπλή να φαίνεται απειροελάχιστη, όπως στον Ευκλείδειο χώρο όχι μόνο ομαλά, αλλά και ως χώρος affine.

Σε κάθε πολλαπλή θετική διάσταση υπάρχουν απείρως πολλές affine συνδέσεις. Εάν η πολλαπλή είναι περαιτέρω προικισμένη με μια Riemannian μετρικό τότε υπάρχει μια φυσική επιλογή σύνδεσης affine, που ονομάζεται η σύνδεση Levi-Civita. Η επιλογή μιας σύνδεσης affine είναι ισοδύναμη με τη συνταγογράφηση, έναν τρόπο διαφοροποίησης των πεδίων φορέα ο οποίος πληροί αρκετές λογικές ιδιότητες (γραμμικότητα και ο κανόνας του Leibniz). Αυτό δίνει έναν πιθανό ορισμό μιας σύνδεσης affine ως coveriant παράγωγο ή (γραμμική) σχέση στη δέσμη εφαπτομένης. Μια ακόμη επιλογή των affine συνδέσεων είναι ότι είναι ισοδύναμο με μια έννοια της παράλληλης μεταφοράς, το οποίο είναι μια μέθοδος για τη μεταφορά διανυσμάτων εφαπτομένης κατά μήκος καμπυλών. Αυτό καθορίζει επίσης μια παράλληλη μεταφορά στη δέσμη πλαισίου. Απειροελάχιστη παράλληλη μεταφορά στη δέσμη πλαισίου δίνει μια άλλη περιγραφή μιας σύνδεσης affine, είτε ως μια σύνδεση Cartan για την ομάδα affine ή ως κύρια σύνδεση στη δέσμη πλαισίου.

Οι κύριες ιδιότητες μιας σύνδεσης affine είναι η στρέψη και καμπυλότητα της. Τα μέτρα στρέψης ανάλογα με το πόσο στενά συνδεδεμένα είναι με το στήριγμα Lie των διανυσματικών πεδίων μπορεί να ανακτηθεί από τη σύνδεση affine. Συνδέσεις affine μπορούν επίσης να χρησιμοποιηθούν για να καθορίσουν (affine) geodesics σε ένα συλλέκτη, γενικεύοντας τις ευθείες γραμμές στον Ευκλείδειο χώρο, αν και η γεωμετρία των εν λόγω ευθειών γραμμών μπορεί να είναι πολύ διαφορετική από τη συνηθισμένη Ευκλείδεια γεωμετρία. Οι κύριες διαφορές συνοψίζονται στην καμπυλότητα της σύνδεσης.

Κίνητρα και ιστορία

Μια ομαλή πολλαπλή είναι ένα μαθηματικό αντικείμενο που μοιάζει τοπικά σαν μια ομαλή παραμόρφωση του Ευκλείδειου χώρου R^n: για παράδειγμα, μια ομαλή καμπύλη ή επιφάνεια φαίνεται τοπικά σαν μια ομαλή παραμόρφωση μιας γραμμής ή ενός επιπέδου. Ομαλή λειτουργία και διανυσματικά πεδία μπορούν να οριστούν σε πολλαπλότητες, όπως ακριβώς συμβαίνει στην Ευκλείδειο χώρο, και οι βαθμωτές λειτουργίες σε πολλαπλότητες μπορούν να διαφοροποιηθούν σε ένα φυσικό τρόπο. Ωστόσο, η διαφοροποίηση των διανυσματικών πεδίων είναι λιγότερο απλή: αυτό είναι ένα απλό θέμα στον Ευκλείδειο χώρο, επειδή ο χώρος εφαπτομένων φορέων που βασίζονται σε ένα σημείο Ρ μπορεί να προσδιοριστεί με φυσικό τρόπο (με μετάφραση) με το χώρο εφαπτομένης σε ένα κοντινό σημείο q. Σε γενικές γραμμές πολλαπλή, δεν υπάρχει τέτοια φυσική ταυτοποίηση των χώρων γύρω από το χώρο εφαπτομένης, και έτσι οι φορείς της εφαπτομένης σε κοντινά σημεία δεν μπορούν να συγκριθούν με έναν καλά καθορισμένο τρόπο. Η έννοια της σύνδεσης affine εισήχθη για την αντιμετώπιση αυτού του προβλήματος συνδέοντας κοντινά διαστήματα εφαπτομένης. Η προέλευση αυτής της ιδέας μπορεί να αναχθεί σε δύο κύριες πηγές: θεωρία επιφάνειας και tensor λογισμός.

Κίνητρα από την θεωρία της επιφάνειας

Σκεφτείτε μια λεία επιφάνεια S σε τρισδιάστατο Ευκλείδειο χώρο. Κοντά σε οποιοδήποτε σημείο,το S μπορεί να προσεγγιστεί από το εφαπτόμενο επίπεδο της σε εκείνο το σημείο, το οποίο είναι ένας συσχετισμένος υποχώρος του Ευκλείδειου χώρου. Διαφορικοί γεωμέτρες τον 19ο αιώνα ενδιαφέρονταν για την έννοια της ανάπτυξης στην οποία μία επιφάνεια κυλιόταν μαζί με μια άλλη, χωρίς να γλιστρά ή συστρέφεται. Ειδικότερα, το εφαπτόμενο επίπεδο προς ένα σημείο του S μπορεί να τυλίγεται στο S: είναι εύκολο να φανταστεί κανείς, όταν το S είναι μία επιφάνεια, όπως η 2-σφαίρας, η οποία είναι το λείο σύνορο μιας κυρτής περιοχής. Δεδομένου ότι το εφαπτόμενο επίπεδο είναι τυλιγμένο στο S, το σημείο επαφής είναι ίχνος μιας καμπύλης στο S. Αντίθετα, δίνεται μια καμπύλη στο S, το εφαπτόμενο επίπεδο μπορεί να τυλίγεται κατά μήκος αυτής της καμπύλης. Αυτό παρέχει έναν τρόπο για τον προσδιορισμό των επιπέδων εφαπτομένης σε διάφορα σημεία κατά μήκος της καμπύλης: συγκεκριμένα, ένας φορέας εφαπτομένης στο χώρο εφαπτομένης σε ένα σημείο επί της καμπύλης ταυτοποιείται με ένα μοναδικό φορέα εφαπτομένης σε οποιοδήποτε άλλο σημείο πάνω στην καμπύλη. Αυτές οι ταυτοποιήσεις δίνονται πάντα με affine μετασχηματισμούς από ένα εφαπτόμενο επίπεδο στο άλλο.

Αυτή η έννοια της παράλληλης μεταφοράς των φορέων εφαπτομένης, από συσχετισμένους μετασχηματισμούς, κατά μήκος μιας καμπύλης έχει ένα χαρακτηριστικό γνώρισμα: το σημείο επαφής της εφαπτομένης του επιπέδου με την επιφάνεια κινείται πάντα με την καμπύλη υπό παράλληλη μετάφραση (δηλαδή, όπως το εφαπτόμενο επίπεδο κυλίεται κατά μήκος της επιφάνειας,κινείται και το σημείο επαφής ). Αυτή η γενική κατάσταση είναι χαρακτηριστικό της Cartan σύνδεσης. Σε πιο σύγχρονες προσεγγίσεις, το σημείο επαφής θεωρείται ως η προέλευση του εφαπτόμενου επίπεδου (το οποίο στη συνέχεια είναι ένας διανυσματικός χώρος), και η κίνηση της καταγωγής διορθώνεται από μετάφραση, έτσι ώστε η παράλληλη μεταφορά να είναι γραμμική, παρά affine.

Κατά την άποψη της Cartan σύνδεσης, ωστόσο, οι affine υπoχώροι του Ευκλείδειου χώρου είναι μοντέλο επιφάνειας - είναι οι πιο απλές επιφάνειες σε Ευκλείδειο 3-χώρο, και είναι ομοιογενείς στην ομάδα affine επιπέδων - και σε κάθε λεία επιφάνεια έχει ένα μοναδικό μοντέλο επιφάνειας εφαπτόμενο σε αυτό σε κάθε σημείο. Αυτές οι επιφάνειες είναι μοντέλο Klein γεωμετρίας κατά την έννοια του προγράμματος Erlangen Felix Klein. Γενικότερα, ένας n-διάστατος χώρο affine είναι μια γεωμετρία Klein για την ομάδα affine Aff (n), ο σταθεροποιητής ενός σημείου είναι η γενική γραμμική ομάδα GL (n). Ένας συσχετισμένος n-συλλέκτη είναι τότε ένας συλλέκτης που μοιάζει απειροελάχιστα στις διαστάσεις affine χώρου.

Κίνητρα από tensor λογισμό

Το δεύτερο κίνητρο για συνδέσεις affine προέρχεται από την έννοια της covariant παραγώγου διανυσματικών πεδίων. Πριν από την έλευση των συντεταγμένων-ανεξάρτητων μεθόδων, ήταν απαραίτητο να συνεργαστεί με τα πεδία φορέων χρησιμοποιώντας τα συστατικά τους σε διαγράμματα συντεταγμένων. Αυτά τα στοιχεία μπορούν να διαφοροποιηθούν, αλλά τα παράγωγα δεν μετατρέπονται σε έναν εύχρηστο τρόπο κάτω από τις αλλαγές των συντεταγμένων. Διορθωτικοί όροι εισήχθησαν από τον Elwin Bruno Christoffel (μετά από τις ιδέες του Bernhard Riemann) το 1870, έτσι ώστε το (διορθωμένο) παράγωγο ενός διανυσματικού πεδίου κατά μήκος να μετατραπεί σε covariantly κάτω από μετασχηματισμούς συντεταγμένων - αυτοί οι όροι διόρθωσης στη συνέχεια έγιναν γνωστοί ως σύμβολα Christoffel. Αυτή η ιδέα αναπτύχθηκε στη θεωρία του απόλυτου διαφορικού λογισμού (γνωστή σήμερα ως tensor λογισμός) από Gregorio Ricci-Curbastro και μαθητής του Tullio Levi-Civita μεταξύ 1880 και αρχές του 20ου αιώνα.

Ο tensor λογισμός πραγματικά ήρθε στη ζωή με την έλευση της θεωρίας της γενικής σχετικότητας το 1915 Άλμπερτ Αϊνστάιν. Λίγα χρόνια μετά από αυτό, Levi-Civita επισημοποίησε τη μοναδική σύνδεση που σχετιζόταν με το Riemannian μετρικό, τώρα γνωστή ως σύνδεση Levi-Civita . Περισσότερες γενικές affine συνδέσεις μελετήθηκαν στη συνέχεια γύρω στο 1920, από τον Hermann Weyl, ο οποίος ανέπτυξε μια λεπτομερή μαθηματική βάση για τη γενική σχετικότητα, και από τον Élie Cartan, ο οποίος έκανε τη σύνδεση με τις γεωμετρικές ιδέες που προέρχονται από τη θεωρία επιφάνεια.

Προσεγγίσεις

Το σύμπλεγμα των ιστοριών έχει οδηγήσει στην ανάπτυξη διαφορετικών προσεγγίσεων και γενικεύσεων της affine σύνδεσης.

Η πιο δημοφιλής προσέγγιση είναι ίσως ο ορισμός του covariant παραγώγου. Από τη μία πλευρά, οι ιδέες του Weyl παρελήφθησαν από τους φυσικούς, με τη μορφή της θεωρίας βαθμίδας και της θεωρίας των covariant παραγώγων. Από την άλλη πλευρά, η έννοια της covariant διαφοροποίησης αποσπάται από τον Jean-Louis Koszul, ο οποίος ορίζει (γραμμικές ή Koszul) συνδέσεις στο φορέα δεσμών. Σε αυτή τη γλώσσα, μια σύνδεση affine είναι απλά ένα covariant παράγωγο ή (γραμμική) σχέση στη δέσμη εφαπτομένης.

Ωστόσο, η προσέγγιση αυτή δεν εξηγεί τη γεωμετρία στις συνδέσεις affine ούτε πώς απέκτησε το όνομά τους. Ο όρος έχει πραγματικά τις ρίζες του στον εντοπισμό των χώρων εφαπτομένης στη\ον Ευκλείδειο χώρο με τη μετάφραση: αυτή η ιδιότητα σημαίνει ότι το Ευκλείδειο n-επίπεδο είναι ένας affine χώρος. ( Εναλλακτικά, ο Ευκλείδειος χώρος είναι ένας κύριος ομοιογενής χώρος ή torsor κάτω από την ομάδα των μεταφράσεων, η οποία είναι μια υποομάδα της ομάδας affine). Όπως αναφέρθηκε στην εισαγωγή, υπάρχουν διάφοροι τρόποι για να κάνει αυτό ακριβώς: κάποιος χρησιμοποιεί το γεγονός ότι μια affine σύνδεση ορίζει μία έννοια της παράλληλης μεταφοράς των διανυσματικών πεδίων κατά μήκος μιας καμπύλης. Αυτό καθορίζει επίσης μια παράλληλη μεταφορά στη δέσμη πλαισίου. Απειροελάχιστη παράλληλη μεταφορά στη δέσμη πλαίσιο δίνει μια άλλη περιγραφή μιας σύνδεσης affine, είτε ως μια σύνδεση Cartan για την ομάδα affine υποθέσεων (n) ή ως κύριος GL (n) σύνδεση στη δέσμη πλαισίου.

Επίσημος ορισμός ως διαφόρικος τλεστής

Έστω Μ μια ομαλή πολλαπλή και έστω C ∞ (M, TM) είναι ο χώρος των διανυσματικών πεδίων στο M, δηλαδή, ο χώρος του ομαλών τομέων της TM δέσμης εφαπτομένης. Στη συνέχεια, μια affine σύνδεση στο M είναι μια διγραμμική απεικόνιση

${\begin{matrix}C^{\infty }(M,TM)\times C^{\infty }(M,TM)&\rightarrow &C^{\infty }(M,TM)\\(X,Y)&\mapsto &\nabla _{X}Y,\end{matrix}}$

τέτοιες ώστε για όλες τις ομαλές συναρτήσεις f σε C^∞(M,R) και όλα τα πεδία του φορέα X, Y στο M:

1. $\nabla _{fX}Y=f\nabla _{X}Y$, δηλαδή, ∇ είναι C^∞(M,R)-γραμμική στην πρώτη μεταβλητή
2. $\nabla _{X}(fY)=\mathrm {d} f(X)Y+f\nabla _{X}Y$, δηλαδή, ∇ satisfies Leibniz rule στη δεύτερη μεταβλητή.

Στοιχειώδης ιδιότητες

•Όπως προκύπτει από το κατάλυμα (1) η αξία των∇_XY σε ένα σημείο x ∈ M εξαρτάται μόνο από την αξία της Χ στο Χ και όχι στην αξία των Χ στο Μ - { Χ}. Προκύπτει επίσης από το κατάλυμα (2) προκύπτει ότι η αξία των ∇_xY σε ένα σημείο X ∈ M εξαρτάται μόνο από την αξία του Υ σε μια γειτονιά της Χ.

•Αν ∇¹, ∇² είναι συσχετισμένα συνδέσεις τότε η τιμή στο Χ του ∇¹_XY − ∇²_XY μπορεί να γραφεί Γ_x(X_x,Y_x) όπου ::Γ_x: T_xM × T_xM → T_xM

είναι διγραμμική και εξαρτάται ομαλά στο Χ (δηλαδή, καθορίζει μια ομαλή δέσμη homomorphism). Αντιστρόφως, αν ∇ είναι σύνδεση affine και Γ είναι μια τέτοια ομαλή homomorphism δέσμη διγραμμική (ονομάζεται μορφή σύνδεσης στο Μ), τότε ∇+Γ είναι μια σύνδεση affine.

•Αν Μ είναι ένα ανοικτό υποσύνολο του R^n, τότε η δέσμη εφαπτομένης του Μ είναι η ασήμαντη δέσμη M×Rⁿ. Σε αυτή την κατάσταση υπάρχει μια κανονική affine σύνδεση δ στο M: οποιοδήποτε πεδίο διάνυσμα Υ δίνεται από την ομαλή λειτουργία V από M έως R^n: τότε δ_XY είναι το διανυσματικό πεδίο που αντιστοιχεί στην ομαλή λειτουργία δV(Χ)=∂XY από το Μ στο R^n. Οποιαδήποτε άλλη affine σύνδεση ∇ στο M μπορεί επομένως να γραφτεί ∇ = d + Γ, όπου Γ είναι μια μορφή σύνδεσης στο Μ.

•Γενικότερα, ένας τοπικός ευτελισμός της δέσμης εφαπτομένης είναι ένας ισομορφισμός δέσμη μεταξύ του περιορισμού της ΤΜ σε ένα ανοικτό υποσύνολο U του M, και U × R^n. Ο περιορισμός της σύνδεσης affine ∇ σε U μπορεί να γραφεί υπό τη μορφή δ + Γ, όπου Γ είναι μια μορφή σύνδεσης στο U.

Παράλληλη μεταφορά για τις συνδέσεις Affine

Παράλληλη μεταφορά ενός φορέα εφαπτομένης κατά μήκος μιας καμπύλης στον τομέα.

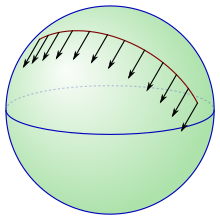
Σύγκριση των διανυσμάτων εφαπτομένης σε διαφορετικά σημεία σε μια πολλαπλή δεν είναι γενικά μια καλά καθορισμένη διαδικασία. Μια affine σύνδεση παρέχει έναn τρόπο να διορθωθεί αυτό χρησιμοποιώντας την έννοια της ̪παράλληλης μεταφορά, και μάλιστα αυτό μπορεί να χρησιμοποιηθεί για να δώσει έναν ορισμό μιας σύνδεσης affine.

Έστω Μ μία πολλαπλή με μία affine σύνδεση ∇. Τότε ένας φορέας πεδίου Χ λέγεται ότι είναι παράλληλες αν ∇ Χ = 0 με την έννοια ότι για οποιοδήποτε πεδίο διάνυσμα Υ, ∇ ΥΧ = 0. Διαισθητικά μιλώντας, παράλληλoi φορείς έχουν όλα τα παράγωγά τους ίσα με μηδέν και, συνεπώς, κατά κάποιο τρόπο σταθερό. Με την αξιολόγηση ένα παράλληλο διανυσματικό πεδίο σε δύο σημεία Χ και Υ,επιτυγχάνει μια ταυτοποίηση μεταξύ ενός φορέα εφαπτομένης στο χ και μία στο y. Τέτοιοι φορείς εφαπτομένης λέγονται ότι είναι παράλληλες μεταφορές από την άλλη.

Δυστυχώς, μη μηδενικά παράλληλα διανυσματικά πεδία δεν έχουν, σε γενικές γραμμές, ύπαρξη, γιατί η εξίσωση ∇ Χ = 0 είναι μία μερική διαφορική εξίσωση η οποία είναι υπερβολικά καθορισμένη: η προϋπόθεση για ολοκληρωσιμότητα αυτής της εξίσωσης είναι η εξαφάνιση της καμπυλότητας ∇ (βλέπε κατωτέρω). Ωστόσο, αν αυτή η εξίσωση περιορίζεται σε μία καμπύλη από x έως y γίνεται μία συνηθισμένη διαφορική εξίσωση. Υπάρχει τότε μια μοναδική λύση για κάθε αρχική τιμή του Χ στο x.

Ακριβέστερα, αν γ: I → M μια ομαλή καμπύλη μέσω παραμέτρων από ένα διάστημα [a, b] και ξ ∈ ΤχM, όπου χ = γ (α), τότε ένα διανυσματικό πεδίο Χ μήκος γ (και συγκεκριμένα, η αξία αυτή διανυσματικό πεδίο στο y = γ (β)) καλείται η παράλληλη μεταφορά του ξ κατά μήκος y εάν

 1.∇γ(t)Χ=0 , για t ∈ [α,β]
 2.Χγ(α)=ξ.

Επισήμως, η πρώτη προϋπόθεση σημαίνει ότι το Χ είναι παράλληλο σε σχέση με τη υποχώρηση σύνδεση στην υποχώρηση δέσμη γ * ΤΜ. Ωστόσο,σε ένα τοπικό trivialization είναι ένα σύστημα πρώτης τάξης των γραμμικών συνήθων διαφορικών εξισώσεων, η οποία έχει μία μοναδική λύση για κάθε αρχική κατάσταση δίνεται από τη δεύτερη προϋπόθεση (για παράδειγμα, από το θεώρημα Picard-Lindelöf).

Έτσι η παράλληλη μεταφορά παρέχει έναν τρόπο κινούμενων φορέων εφαπτομένης κατά μήκος μιας καμπύλης χρησιμοποιώντας τη σύνδεση affine να τους κρατήσει "δείχνουν προς την ίδια κατεύθυνση" σε μια διαισθητική έννοια, και αυτό παρέχει έναν γραμμικό ισομορφισμό μεταξύ των χώρων της εφαπτόμενης στα δύο άκρα της καμπύλης. Ο ισομορφισμός που λαμβάνεται με αυτόν τον τρόπο γενικά θα εξαρτάται από την επιλογή της καμπύλης: αν δεν το κάνει, τότε παράλληλες μεταφορές κατά μήκος κάθε καμπύλης μπορεί να χρησιμοποιηθεί για να καθορίσει παράλληλα διανυσματικά πεδία σε m, το οποίο μπορεί να συμβεί μόνο εάν η καμπυλότητα του ∇ είναι μηδέν .

Ένας γραμμικός ισομορφισμός καθορίζεται από τη δράση της σε μια διατεταγμένη βάση ή πλαίσιο. Ως εκ τούτου, παράλληλη μεταφορά μπορεί επίσης να χαρακτηριστεί ως ένας τρόπος για τη μεταφορά των στοιχείων (εφαπτομένης) ̪δέσμη πλαισίων GL(Μ) κατά μήκος μιας καμπύλης. Με άλλα λόγια, η σύνδεση affine παρέχει ένα lift για οποιασδήποτε γ καμπύλη σε Μ σε μια καμπύλη γ σε GL(Μ).

Επίσημος ορισμός για τη δέσμη πλαισίων

Μια σύνδεση affine μπορεί επίσης να οριστεί ως κύρια GL (n) σύνδεση ω στη δέσμη πλαισίων FM ή GL(M) ενός συλλέκτη Μ. Με περισσότερες λεπτομέρειες,ω είναι ένας ομαλός χάρτης από την εφαπτόμενη δέσμη T(FM) της δέσμης πλαισίου στο χώρο των ν*ν πινάκων (το οποίο είναι Lie algebra gl (n) από το GL(n) από τους αναστρέψιμους ν*ν πίνακες) ικανοποιώντας δύο ιδιότητες :

    1. το ω είναι  equivariant σε σχέση με τη δράση του GL(n) πάνω στο T(FM) και στο gl(n.
    2. το ω (Χξ) = ξ για οποιοδήποτε ξ στο gl(n), όπου  Χξ είναι το διανυσματικό πεδίο στο  FM αντίστοιχος του ξ.

Μια τέτοια σύνδεση ω ορίζει ,αμέσως, covariant παράγωγο όχι μόνο στη δέσμη εφαπτομένης, αλλά στο διάνυσμα δέσμες που συνδέονται στην κάθε ομάδα εκπροσώπησης από το GL(n), περιλαμβάνοντας δέσμες τανυστών και και tensor πυκνότητες. Αντιστρόφως, μία affine σύνδεση εφαπτόμενη δέσμη καθορίζει μία affine σύνδεση στη δέσμη πλαίσιο, για παράδειγμα ,απαιτώντας ό,τι το ω εξαφανίζεται σε φορείς εφαπτομένης στους ανελκυστήρες των καμπυλών στη δέσμη πλαισίου ορίζεται από παράλληλες μεταφορές. Η δέσμη πλαίσιο έρχεται επίσης εξοπλισμένη με μία μορφή συγκόλλησης θ : T(FM) → Rn η οποία είναι οριζόντια υπό την έννοια ότι εξαφανίζεται για τους κάθετους φορείς όπως οι αξίες σημείο των διανυσματικών πεδίων Χξ: πράγματι, θ ορίζεται πρώτα με την προβολή ενός φορέα εφαπτομένης(σε FM σε ένα πλαίσιο f)στο Μ, στη συνέχεια, με τη λήψη των συστατικών αυτού του φορέα εφαπτομένης στο Μ σε σχέση με το πλαίσιο f. Σημειώστε ότι θ είναι επίσης GL (n)-equivariant (όπου GL (n) ενεργεί εξ Rn από τον πολλαπλασιασμό της μήτρας).Το ζεύγος (θ, ω) ορίζουν μια δέσμη ισομορφισμός Τ (FM) με την τετριμμένη δέσμη Τ (FM) με την ασήμαντη δέσμη FM × aff(n), όπου aff(n) είναι το καρτεσιανό γινόμενο του Rn και gl (n) (θεωρείται ως η άλγεβρα Lie της ομάδας affine, η οποία είναι στην πραγματικότητα μία ημιευθέα προϊόντος - βλ. παρακάτω).

Affine συνδέσεις ως Cartan συνδέσεις

Affine συνδέσεις μπορούν να ορίζονται στο πλαίσιο γενικού πλαισίου Cartan του. 4Στη σύγχρονη προσέγγιση, αυτό έχει στενή σχέση με τον ορισμό των συνδέσεων affine στη δέσμη πλαισίου.Πράγματι, σε μια σύνθεση, μια σύνδεση Cartan είναι ένας απόλυτος παραλληλισμός της κύριας δέσμης ικανοποιώντας κατάλληλες ιδιότητες.Από αυτή την άποψη, ο aff (n)-αξίας 1-μορφή (θ, ω): T (FM) → aff (n) στη δέσμη πλαίσιο (μιας πολλαπλής affine) είναι μια σύνδεση Cartan. Ωστόσο, η αρχική προσέγγιση Cartan ήταν διαφορετικό από αυτό σε μια σειρά από τρόπους:

   • η έννοια των δεσμών πλαισίου ή οι κύριες δέσμες δεν υπάρχουν
   • μια σύνδεση θεωρήθηκε από την άποψη της παράλληλης μεταφοράς μεταξύ απειροελάχιστα κοντινά σημεία 5
   • αυτή η παράλληλη μεταφορά ήταν συσχετισμένη, και όχι γραμμική
   • τα αντικείμενα που μεταφέρονται δεν ήταν φορείς εφαπτομένης με τη σύγχρονη έννοια, αλλά και τα στοιχεία ενός χώρου affine με                      σημαδεμένο σημείο, το οποίο η σύνδεση Cartan προσδιορίζει τελικά με το χώρο εφαπτομένης.

Επεξηγήσεις και ιστορική διαίσθηση

Τα σημεία που έθεσε μόνο είναι εύκολο να εξηγήσουμε την ανάποδη, ξεκινώντας από τα κίνητρα που παρέχονται από τη θεωρία της επιφάνειας. Σε αυτήν την κατάσταση, αν και τα αεροπλάνα να κυλήσουν πάνω από την επιφάνεια είναι εφαπτόμενα επίπεδα σε μια αφελή έννοια, η έννοια ενός χώρου εφαπτομένης είναι πραγματικά μία απειροελάχιστη έννοια, 6, ενώ τα επίπεδα, όπως affine υπόχωροι του R3, είναι άπειρα σε έκταση.Ωστόσο, αυτά τα συσχετισμένα αεροπλάνα έχουν όλα ένα σημαδεμένο σημείο, το σημείο επαφής με την επιφάνεια, και είναι εφαπτόμενα στην επιφάνεια σε αυτό το σημείο. Κατά συνέπεια, η σύγχυση προκύπτει επειδή ένας affine χώρος συσχετισμένος με ένα σημαδεμένο σημείο μπορεί να ταυτιστεί με τον εφαπτόμενο χώρο του σε εκείνο το σημείο. Ωστόσο, η παράλληλη μεταφορά ορίζεται από τροχαίο δεν διορθώνει αυτήν την "καταγωγή":είναι συσχετισμένη και όχι γραμμική,η γραμμική παράλληλη μεταφορά μπορεί να ανακτηθεί εφαρμόζοντας μια μετάφραση.Αφαιρώντας αυτήν την ιδέα, ένας συσχετισμένος συλλέκτης θα πρέπει να είναι μια n-πολλαπλότητα M με ένα βελτιωμένο χώρο Ax,διάστασης n, που επισυνάπτεται σε κάθε x ∈ M σε ένα επισημασμένο σημείο ax ∈ Ax,μαζί με μία μέθοδο για τη μεταφορά των εν λόγω στοιχείων affine χώρους κατά μήκος κάθε καμπύλης C σε Μ. Αυτή η μέθοδος απαιτείται για να ικανοποιήσει πολλές ιδιότητες:

  1.για οποιαδήποτε δύο σημεία x, y στο C, παράλληλη μεταφορά είναι ένας συσχετισμένος μετασχηματισμός από Ax σε Ay
  2.παράλληλη μεταφορά ορίζεται απειροστά υπό την έννοια ότι είναι διαφορίσιμη σε κάθε σημείο C και εξαρτάται μόνο από τον φορέα εφαπτομένη C σε εκείνο το σημείο
  3.η παράγωγος της παράλληλης μεταφοράς στο x καθορίζει έναν γραμμικό ισομορφισμό από  TxM to T_{a_x}A_x.

Αυτά τα δύο τελευταία σημεία είναι αρκετά δύσκολο να γίνουν ακριβείς, 7, έτσι affine συνδέσεις ορίζονται απειροελάχιστα.Για να παρακινήσει αυτό, αρκεί να εξετάσουμε πώς συσχετισμένα πλαίσια αναφοράς μετατρέπονται απειροελάχιστα σε σχέση με την παράλληλη μεταφορά.(Αυτή είναι η προέλευση της μεθόδου Cartan της μετακίνησης πλαισίων.)Ένα πλαίσιο affine σε ένα σημείο αποτελείται από μια λίστα (ρ, e1, ..., en), όπου p ∈ Ax 8 και οι ei αποτελούν τη βάση του Tp (Ax). Η σύνδεση affine συνέχεια δίνεται συμβολικά από ένα πρώτης τάξης διαφορικό σύστημα.

Επιπλέον, οι χώροι affine Ax απαιτείται να είναι εφαπτομένη Μ στην άτυπη έννοια ότι η μετατόπιση κατά μήκος ax γ μπορεί να προσδιοριστεί (περίπου ή απειροστά) με τον φορέα εφαπτομένης γ '(t) στο γ σε χ = γ (t) (η οποία είναι η απειροελάχιστη μετατόπιση του Χ).Από

ax (γ (t + δt)) - ax (γ (t)) = θ (γ '(t)) δt, όπου θ ορίζεται από θ (Χ) = θ1 (Χ) e1 + ... + θn (Χ) en, αυτή η αναγνώριση δίνεται από θ, οπότε η απαίτηση είναι ότι θ πρέπει να είναι ένας γραμμικός ισομορφισμός σε κάθε σημείο.

Η εφαπτόμενη affine χώρο Ax, χαρακτηρίζεται επομένως διαισθητικά με ένα απειροελάχιστο affine γειτονιά του x. Η σύγχρονη άποψη κάνει όλη αυτή τη διαίσθηση πιο ακριβή χρησιμοποιώντας κύριες δέσμες (η βασική ιδέα είναι να αντικατασταθεί ένα πλαίσιο ή ένα μεταβλητό πλαίσιο από το χώρο όλων των πλαισίων και των λειτουργιών σε αυτό το διάστημα).Εμπνέεται επίσης από την έμπνευση του προγράμματος Erlangen Felix Klein, 9, στην οποία μια γεωμετρία ορίζεται να είναι ένα ομοιογενές χώρος. Affine χώρος είναι μια γεωμετρία με αυτή την έννοια, και είναι εξοπλισμένος με μια επίπεδη σύνδεση Cartan. Έτσι, μια γενική affine πολλαπλή θεωρείται ως καμπύλο παραμόρφωση της επίπεδης γεωμετρίας ενός μοντέλου του affine χώρου.

Ορισμός ως χώρου affine

Ανεπίσημα, ένας χώρος affine είναι ένας διανυσματικός χώρος χωρίς σταθερή επιλογή της προέλευσης. Περιγράφει τη γεωμετρία των σημείων και ελεύθερα διανύσματα στο χώρο.Ως συνέπεια της έλλειψης προέλευσης, τα σημεία στο συσχετισμένο χώρο δεν μπορούν να προστεθούν μαζί, καθώς αυτό απαιτεί επιλογή προέλευσης με το οποίο για να σχηματίσει το νόμο παραλληλογράμμου για την προσθήκη φορέα. Ωστόσο, ένα διάνυσμα v μπορεί να προστεθεί σε ένα σημείο Ρ με την τοποθέτηση του αρχικού σημείου του φορέα σε ρ και στη συνέχεια μεταφέροντας το ρ στο τερματικό σημείο .Η διαδικασία που περιγράφεται έτσι p → p + v είναι η μετάφραση του p κατά μήκος ν. Με τεχνικούς όρους, συσχετισμένο n-χώρο είναι ένα σύνολο An εξοπλισμένο με δωρεάν μεταβατική δράση της ομάδας φορέα Rn σε αυτό μέσω αυτής της πράξης της μετάφρασης των σημείων: ένα είναι συνεπώς ένας κύριος ομοιογενής χώρος για το φορέα της ομάδας Rn.

Η γενική γραμμική ομάδα GL (n) είναι η ομάδα των μετασχηματισμών του Rn που διατηρούν τη γραμμική δομή του Rn, υπό την έννοια ότι το Τ (AV + bw) = aT (ν) + bT (νν). Κατ 'αναλογία, η ομάδα affine Aff (n) είναι η ομάδα των μετασχηματισμών An διατηρώντας τη δομή affine.Έτσι, φ ∈ Aff (n) πρέπει να διατηρήσει τις μεταφράσεις, με την έννοια ότι

όπου Τ είναι ένας γενικός γραμμικός μετασχηματισμός.Ο χάρτης αποστολής φ ∈ Aff (n) T ∈ GL (n) είναι ομομορφισμός ομάδα.Ο πυρήνας της είναι η ομάδα των μεταφράσεων Rn. Ο σταθεροποιητής οποιουδήποτε σημείου p στο Α μπορεί έτσι να προσδιοριστεί με GL (n) χρησιμοποιώντας αυτήν την προεξοχή: αυτό αντιλαμβάνεται την ομάδα affine ως ημιευθέα προϊόν της GL (n) και Rn, και affine χώρο ως το ομογενές χώρο Aff (n) / GL (n).

Affine πλαίσια και η επίπεδη affine σύνδεση

Ένα πλαίσιο για affine Α αποτελείται από ένα σημείο p ∈ Α και μια βάση (e1, ..., en) του διανύσματοτικου χώρου ΤρΑ = Rn. Η γενική γραμμική ομάδα GL (n) ενεργεί ελεύθερα στο σύνολο FA όλων των πλαισίων affine με τον καθορισμό ρ και μετατρέποντας τη βάση (e1, ..., en) κατά τον συνήθη τρόπο, και ο χάρτης π στέλνοντας ένα πλαίσιο affine (ρ? e1, ..., en) στο p είναι το πηλίκο του χάρτη.Έτσι FA είναι ένα κύριο GL (n)-πακέτο πάνω Α. Η δράση του GL (n) εκτείνεται φυσικά σε μια ελεύθερη δράση μεταβατικό της ομάδας affine Aff (n) με FA, έτσι ώστε ΦΑ είναι ένα Aff (Ν)-torsor , και η επιλογή ενός πλαισίου αναφοράς προσδιορίζει FA → A με την κύρια δέσμη Aff (n) → Aff (n) / GL (n).

Στις FA υπάρχει μια συλλογή από n +1 συναρτήσεις που ορίζονται από

Μετά την επιλογή ενός basepoint για το Α, όλα αυτά είναι συναρτήσεις με τιμές στο Rn, έτσι ώστε να είναι δυνατόν να ληφθούν εξωτερικές παράγωγοί τους για να ληφθεί διαφορικό 1-μορφές με τιμές στον Rn. Δεδομένου ότι οι λειτουργίες εi δώσει μια βάση για Rn σε κάθε σημείο της FA, οι 1-μορφές πρέπει να εκφραστεί ως αθροίσματα της μορφής

για κάποια συλλογή (θi, ωjk) 1 ≤ i, j, k ≤ n της πραγματικής τιμής ενός- τύπου σε Aff (n). Αυτό το σύστημα του ενός τύπου για την κύρια δέσμη FA → Α ορίζει την σύνδεση affine στο A.

Λαμβάνοντας την εξωτερική παράγωγο δεύτερη φορά, και χρησιμοποιώντας το γεγονός ότι d2 = 0, καθώς και τη γραμμική ανεξαρτησία της εi, οι ακόλουθες σχέσεις λαμβάνονται:

Αυτές είναι οι εξισώσεις Maurer-Cartan για την ομάδα Lie Aff (n) (ταυτίζεται με FA με την επιλογή ενός πλαισίου αναφοράς). Επιπλέον:

      •το σύστημα Pfaffian θj = 0 (για όλα τα j) είναι ολοκληρώσιμη, και ολοκληρωμένη πολλαπλότητες του είναι οι ίνες της κύριας δέσμη Aff (n)   → A.
      •το σύστημα Pfaffian ωij = 0 (για όλα τα i, j) είναι επίσης ολοκληρώσιμη, και αναπόσπαστο πολλαπλότητες της ορισμό του παράλληλου μεταφορών στην FA.

Έτσι, οι τύπου (ωij) ορίζουν μια επίπεδη κύρια σύνδεση στο FA → Α.

Για μια αυστηρή σύγκριση με το κίνητρο, θα πρέπει να καθορίσει πραγματικά παράλληλη μεταφορά στην κύρια Aff (n)-δέσμη πάνω από Α.

Αυτό μπορεί να γίνει με το τράβηγμα πίσω FA από τον ομαλό χάρτης φ: Rn × A → Α που ορίζεται από τη μετάφραση. Στη συνέχεια, το σύνθετο φ '* FA FA → → Α είναι ένας κύριος Aff (n)-δέσμη πάνω από Α, και τα έντυπα (θi, ωjk) τραβήξτε προς τα πίσω για να δώσει μια επίπεδη κύρια Aff (n)-σύνδεση σε αυτή τη δέσμη.

Γενικές affine γεωμετρίες: τυπικοί ορισμοί

Ένας χώρος affine, όπως με ουσιαστικά οποιαδήποτε ομαλή γεωμετρία Klein, είναι μια πολλαπλή εξοπλισμένη με επίπεδη σύνδεση Cartan. Περισσότερες γενικές πολλαπλές affine ή γεωμετρίες affine λαμβάνονται εύκολα με τη ρίψη την κατάσταση επιπεδότητα εκφράζονται από τις εξισώσεις Maurer-Cartan.Υπάρχουν διάφοροι τρόποι για να προσεγγίσει τον ορισμό και δύο θα δοθούν. Και οι δύο ορισμοί διευκολύνονται από την συνειδητοποίηση ότι η 1-μορφές (θi, ωjk) σε επίπεδη μοντέλο ταιριάζουν μεταξύ τους για να δώσουν μια 1-μορφή με τιμές στην άλγεβρα Lie υποθέσεων (n) της ομάδας affine Aff (n).

Σε αυτούς τους ορισμούς, το Μ είναι μια ομαλή ν-πολλαπλή και Α = Aff (n) / GL (n) είναι ένας χώρος συσχετισμένος της ίδιας διάστασης.

Ορισμός μέσω απολύτου παραλληλισμού

Έστω Μ ένας συλλέκτης, και P μια κύρια GL (n)-δεσμίδα πάνω M. Στη συνέχεια, μία συσχετισμένη σύνδεση είναι μια 1-μορφή η σε P με τιμές σε υποθέσεων (n) ικανοποιεί τις ακόλουθες ιδιότητες

 1.η είναι equivariant σε σχέση με τη δράση του GL (n) με P και aff (n)
 2.η (Χξ) = ξ για κάθε ξ στο Lie άλγεβρα gl (n) όλων των n × n πινάκων?
 3.η είναι ένας γραμμικός ισομορφισμός του κάθε χώρου που εφάπτεται του P με aff (n).

Ο τελευταίος όρος σημαίνει ότι η είναι μια απόλυτη αμοιβαιότητα σε P, δηλαδή, προσδιορίζει τη δέσμη εφαπτομένης της P με ένα ασήμαντο πακέτο (σε αυτή την περίπτωση P × aff (n)). Το ζεύγος (P, η) καθορίζει τη δομή μιας γεωμετρίας affine στο M, καθιστώντας σε μια πολλαπλή affine.

Η άλγεβρα Lie aff affine (n) χωρίζει ως ημιευθέα προϊόν του Rn και gl (n) και έτσι η μπορεί να γραφτεί ως ένα ζεύγος (θ, ω), όπου θ παίρνει τιμές στο Rn και ω παίρνει τιμές στην gl (n). Οι προϋποθέσεις (1) και (2) είναι ισοδύναμες προς ω είναι ένας κύριος GL (n)-σύνδεση και θ είναι μια οριζόντια equivariant 1-μορφή, η οποία επάγει μία δεσμίδα από ομομορφισμός TM με την πακέτο που σχετίζεται Ρ × GL (n) Rn .Ο όρος (3) είναι ισοδύναμος με το γεγονός ότι αυτή η δέσμη ομορφισμό είναι ισομορφισμός. (Ωστόσο, αυτή η αποσύνθεση είναι μια συνέπεια της ειδικότερη δομή του ομίλου affine.) Δεδομένου ότι το Ρ είναι η δέσμη πλαισίου Ρ × GL (n) Rn, συνάγεται ότι θ παρέχει μια δέσμη ισομορφισμό μεταξύ Ρ και της δέσμης των πλαισίων FM από  Μ_ αυτό ανακτά τον ορισμό μιας σύνδεσης affine ως κύριο GL (n)-σύνδεσης FM από .

Οι 1-μορφές που προκύπτουν στο επίπεδο μοντέλο είναι ακριβώς τα συστατικά του θ και ω.

Ορισμός ως κύρια σύνδεση affine

Μια σύνδεση affine στο M αποτελεί κύρια Aff (n)-δέσμη Q πάνω από M, μαζί με ένα κύριο GL (n)-subbundle P από Q μια κύρια Aff (n)-σύνδεση α (α 1-μορφή Q με τιμές σε aff (n)), η οποία ικανοποιεί την ακόλουθη (generic) Cartan κατάσταση. Το συστατικό του Rn αποχώρηση του α σε P είναι ένα οριζόντιο equivariant 1-μορφή και έτσι ορίζει ένα ομορφισμό δεσμίδα από TM για να P × GL (n) Rn: αυτό που απαιτείται για να είναι ισομορφισμός.

Σχετικά με την δραστηριοποίηση

Δεδομένου Aff (ιδ) επενεργεί επί  Α, υπάρχει, συνδέεται με την κύρια δέσμη Q, μία δέσμη Α = Q × Aff (n) Α, η οποία είναι μια δέσμη ινών πάνω Μ του οποίου οι ίνες στο χ σε Μ είναι ένας συσχετισμένος χώρος Αχ. Ένα τμήμα από ένα Α (ορίζει ένα σημαδεμένο σημείο ax σε Ax για κάθε x ∈ M) καθορίζει μια κύρια GL (n)-subbundle P από Q (όπως η δέσμη των σταθεροποιητών αυτών σημαδεμένων σημείων) και αντιστρόφως.Η κύρια σύνδεση α ορίζει μια σύνδεση Ehresmann σε αυτό το πακέτο, ως εκ τούτου, μια έννοια της παράλληλης μεταφοράς. Η κατάσταση Cartan εξασφαλίζει ότι η διακεκριμένη ενότητα κινείται μια πάντα στο πλαίσιο της παράλληλης μεταφοράς.

Περαιτέρω ιδιότητες

Καμπυλότητα και στρέψη

Καμπυλότητα και στρέψη είναι τα κύρια αναλλοίωτα μιας σύνδεσης affine. Δεδομένου ότι υπάρχουν πολλοί τρόποι για ισοδύναμα να ορισθεί η έννοια της σύνδεσης affine, έτσι υπάρχουν πολλοί διαφορετικοί τρóποι για τον καθορισμó της καμπυλότητας και της στρέψης.

Από το σημείο σύνδεσης Cartan , η καμπυλότητα είναι η αποτυχία της affine τη σύνδεσης με η να ικανοποιούν την εξίσωση Maurer-Cartan

όπου ο δεύτερος όρος στην αριστερή πλευρά είναι το προϊόν επιβάρυνσης με τη βάση Lie σε aff (ιδ) να συνάπτει τις τιμές. Με την επέκταση της η μέσα στο ζεύγος (θ, ω) και χρησιμοποιώντας τη δομή της Lie άλγεβρας aff (n), αυτή η αριστερή πλευρά μπορεί να επεκταθεί σε δύο τύπους

όταν τα προϊόντα επιβάρυνσης αξιολογήθηκαν χρησιμοποιώντας τον πολλαπλασιασμό πινάκων. Η πρώτη έκφραση καλείται η στρέψη της σύνδεσης, και η δεύτερη ονομάζεται επίσης η καμπυλότητα.

Αυτές οι εκφράσεις είναι διαφορικής 2-μορφές στο συνολικό χώρο της μιας δέσμης πλαισίου. Ωστόσο, είναι οριζόντια και equivariant, και ως εκ τούτου καθορίζουν tensorial αντικείμενα. Αυτά μπορούν να καθοριστούν άμεσα από την επαγόμενη συναλλοίωτη παράγωγο ∇ σε ΤΜ ως ακολούθως.

Η στρέψη δίδεται από τον τύπο

Αν η ροπή εξαφανίζεται, η σύνδεση λέγεται ότι είναι στρέψης-ελεύθερη ή συμμετρική.

Η καμπυλότητα δίδεται από τον τύπο

Όταν και οι δύο καμπυλότητα και στρέψη εξαφανίζονται, η σύνδεση καθορίζει τη δομή άλγεβρα προ-Lie άλγεβραξαπλώστε στο χώρο των παγκόσμιων τμημάτων της δέσμης εφαπτομένης.

Η σύνδεση Levi-Civita

Αν (M, g) είναι μια Riemannian πολλαπλή, τότε υπάρχει μια μοναδική affine σύνδεση ∇ στο M με τις ακόλουθες δύο ιδιότητες:

    •η σύνδεση είναι στρέψης χωρίς, δηλαδή, T ∇ είναι μηδέν
    •παράλληλη μεταφορά είναι μια ισομετρία,i.e., δηλαδή, τα εσωτερικά προϊόντα (που ορίζονται χρησιμοποιώντας ζ) μεταξύ των διανυσμάτων εφαπτομένης είναι διατηρημένα.

Αυτή η σύνδεση ονομάζεται η σύνδεση Levi-Civita.

Ο δεύτερος όρος σημαίνει ότι η σύνδεση είναι μια μετρική σχέση με την έννοια ότι το Riemannian μετρικό g είναι παράλληλα:. ∇ g = 0 Σε τοπικές συντεταγμένες τα συστατικά της μορφής σύνδεσης ονομάζονται σύμβολα Christoffel: λόγω της μοναδικότητας του Levi-Civita σύνδεση,i.e., υπάρχει μια φόρμουλα για τα συστατικά αυτά από την άποψη των συστατικών της g.

Γεωδεσιακές

Από ευθείες γραμμές είναι μια έννοια σε affine γεωμετρία,i.e., συνδέσεις affine ορίζουν μια γενικευμένη έννοια της (μέσω παραμέτρων) ευθείες γραμμές σε κάθε πολλαπλή affine, που ονομάζεται affine geodesics. Αφηρημένα,i.e., μια παραμετρική καμπύλη γ: I → M είναι μια ευθεία γραμμή, αν διάνυσμα εφαπτομένης του παραμένει παράλληλο και equipollent με τον εαυτό του όταν μεταφέρεται κατά μήκος της γ.Από τη γραμμική άποψη, μια σύνδεση affine Μ διακρίνει τα geodesics affine με τον ακόλουθο τρόπο: μια ομαλή καμπύλη γ: I → Μ είναι affine γεωδαιτικής αν \ dot \ gamma είναι παράλληλο μεταφέρεται κατά μήκος γ, δηλαδή

$\tau _{t}^{s}{\dot {\gamma }}(s)={\dot {\gamma }}(t)$

όπου τts: ΤγsM → ΤγtM είναι η παράλληλη μεταφορά χάρτη που ορίζει τη σύνδεση.

Όσον αφορά την απειροελάχιστη σύνδεση ∇, η παράγωγος της εξίσωσης προϋποθέτει

$\nabla _{{\dot {\gamma }}(t)}{\dot {\gamma }}(t)=0$ for all t ∈ I

Αντιστρόφως, οποιαδήποτε λύση αυτής της διαφορικής εξίσωσης δίδει μία καμπύλη της οποίας η εφαπτομένη είναι παράλληλη φορέως μεταφέρεται κατά μήκος της καμπύλης. Για κάθε x ∈ M και κάθε X ∈ TXM,i.e., υπάρχει ένα μοναδικό affine γ γεωδαιτικών: I → M με γ (0) = x και \ dot \ gamma (0) = X και όπου Ι είναι το μέγιστο ανοικτό διάστημα στο R, που περιέχει από 0, στην οποία ορίζεται το γεωδαιτικός. Αυτό προκύπτει από το θεώρημα Picard-Lindelöf, και επιτρέπει τον ορισμό μιας εκθετικής στο χάρτη που σχετίζεται με τη σύνδεση affine.

Ειδικότερα, όταν το Μ είναι ένα (ψευδο-) Riemannian πολλαπλή και ∇ είναι η σύνδεση Levi-Civita, τότε το γεωδαιτικό affine είναι οι συνήθεις γεωδαισιακές των Riemannian γεωμετρία και είναι η τοπικά απόσταση ελαχιστοποίηση καμπύλες.

Οι γεωδαιτικές ορίζονται εδώ  μερικές φορές ονομάζονται affinely μέσω παραμέτρων, δεδομένου ότι μία συγκεκριμένη ευθεία γραμμή στο M καθορίζει μια παραμετρική καμπύλη γ μέσω της γραμμής μέχρι μια επιλογή από affine reparametrization γ (t) → γ (στο + b), όπου a και b είναι σταθερές . Ο φορέας εφαπτομένη μιας γεωδαιτικής affine είναι παράλληλος και κατά μήκος equipollent το ίδιο. Μια unparametrized γεωδαιτικός, ή αυτό που είναι απλώς παράλληλα προς την ίδια, χωρίς κατ 'ανάγκην να είναι equipollent, χρειάζεται μόνο να ικανοποιήσουν

$\nabla _{\dot {\gamma }}{\dot {\gamma }}=k{\dot {\gamma }}$

για κάποιο k η συνάρτηση ορίζεται κατα μήκος της γ. Οι Unparametrized γεωδαιτικές συχνά μελετήθηκαν από την άποψη προβολικών συνδέσεων.

Ανάπτυξη

Μια σύνδεση affine ορίζει μια έννοια της ανάπτυξης των καμπυλών. Διαισθητικά, η ανάπτυξη συλλαμβάνει την έννοια ότι, αν xt είναι μια καμπύλη στην M, τότε ο χώρος affine εφαπτομένη στο x0 μπορεί να έλαθει κατά μήκος της καμπύλης. Καθώς το κάνει αυτό, η σήμανση σημείο επαφής μεταξύ του χώρου εφαπτομένης και την πολλαπλή διαγράφει μια καμπύλη Ct σε αυτό το χώρο affine: την ανάπτυξη της xt.Από τυπική άποψη, ας τt0: TxtM → Tx0M είναι η γραμμική παράλληλη χάρτη των μεταφορών που σχετίζονται με τη σύνδεση affine. Τότε η ανάπτυξη Ct είναι η καμπύλη στο Tx0M ξεκινά στις 0 και είναι παράλληλη προς την εφαπτομένη της XT για όλο το χρόνο t:

${\dot {C}}_{t}=\tau _{t}^{0}{\dot {x}}_{t},\quad C_{0}=0.$

Ειδικότερα, xt είναι μια γεωδαισιακή αν και μόνο αν η ανάπτυξή της είναι μια affinely μέσω παραμέτρων ευθεία γραμμή στο Tx0M. [10]

Επιφανειακή θεωρία αναθεωρημένη

Εάν το Μ είναι μια επιφάνεια στο R3, είναι εύκολο να δούμε ότι η M έχει μια φυσική σύνδεση affine. Από το γραμμικό σημείο σύνδεσης του άποψη, η συναλλοίωτη παράγωγο ενός διανυσματικού πεδίου ορίζεται με την διαφοροποίηση της διανυσματικό πεδίο, θεωρείται ως ένα χάρτη από Μ έως R3, και στη συνέχεια, το αποτέλεσμα που προεξέχει ορθογώνια πίσω επάνω από τους χώρους εφαπτομένη Μ. Είναι εύκολο να δείτε ότι αυτή η σύνδεση είναι affine στρέψης-free.Επιπλέον, είναι μια μετρική σύνδεση σε σχέση με την Riemannian μετρικό στο M που επάγεται από το εσωτερικό γινόμενο για τα R3, ως εκ τούτου, είναι η σύνδεση Levi-Civita της παρούσας μετρική.

Παράδειγμα: Η μοναδιαία σφαίρα στο επίπεδο

Ας $\langle ,\rangle$ είναι η συνήθης εσωτερικό γινόμενο στο R3, και αφήστε το S2 είναι η μοναδιαία σφαίρα. Ο χώρος που εφάπτεται με το S2 σε ένα σημείο x είναι φυσικά ταυτίζεται με τον φορέα υπο-χώρο του R3 που αποτελείται από όλα τα διανύσματα ορθογώνια προς x. Συνάγεται ότι ένας φορέας στον τομέα Υ για S2 μπορεί να θεωρηθεί ως ένα Υ χάρτη: S2 → R3 η οποία πληροί

$\langle Y_{x},x\rangle =0,\quad \forall x\in \mathbf {S} ^{2}.$

Συμβολίζουμε με dY το διαφορικό ενός τέτοιου χάρτη. Τότε έχουμε:

Λήμμα. ο τύπος

$(\nabla _{X}Y)_{x}=\mathrm {d} Y_{x}(X)+\langle X_{x},Y_{x}\rangle x\,$

ορίζει μια σύνδεση affine στο S2 με εξαφάνιση στρέψης.

πόδειξη. Είναι εύκολο να αποδείξει ότι ∇ ικανοποιεί την ταυτότητα Leibniz και είναι C ∞ (S2) γραμμική στην πρώτη μεταβλητή. Έτσι, το μόνο που χρειάζεται να αποδειχθεί είναι ότι ο παραπάνω χάρτης δεν ορίζουν πράγματι ένα πεδίο διάνυσμα εφαπτομένης. Δηλαδή, θα πρέπει να αποδείξετε ότι για κάθε x στο S2

$\langle (\nabla _{X}Y)_{x},x\rangle =0\qquad (1).$

Εξετάστε το χάρτη

${\begin{cases}f:\mathbf {S} ^{2}\to \mathbf {R} \\x\longmapsto \langle Y_{x},x\rangle .\end{cases}}$

Ο χάρτης f είναι σταθερή, ως εκ τούτου απόκλιση του εξαφανίζεται. ειδικότερα

$\mathrm {d} f_{x}(X)=\langle (\mathrm {d} Y)_{x}(X),x\rangle +\langle Y_{x},X_{x}\rangle =0.\,$

Η εξίσωση (1) ανωτέρω ακολούθως.