Κανόνας πεπερασμένης υποδιαίρεσης

Προοπτική προβολή ενός δωδεκαεδρικού ψηφιδωτού στο H3. Σηµειώστε την αναδροµική δοµή: κάθε πεντάγωνο περιέχει µικρότερα πεντάγωνα, τα οποία περιέχουν µικρότερα πεντάγωνα. Αυτό είναι ένα παράδειγμα ενός κανόνα υποδιαίρεσης που προκύπτει από ένα πεπερασμένο σύμπαν (δηλ. μια κλειστή 3-πολλαπλότητα).

Στα μαθηματικά, ένας κανόνας πεπερασμένης υποδιαίρεσης είναι ένας αναδρομικός τρόπος διαίρεσης ενός πολυγώνου ή άλλου δισδιάστατου σχήματος σε όλο και μικρότερα τεμάχια. Οι κανόνες υποδιαίρεσης είναι κατά μία έννοια γενικεύσεις των κανονικών γεωμετρικών φράκταλ. Αντί να επαναλαμβάνουν το ίδιο ακριβώς σχέδιο ξανά και ξανά, έχουν μικρές παραλλαγές σε κάθε στάδιο, επιτρέποντας μια πλουσιότερη δομή, διατηρώντας παράλληλα το κομψό ύφος των φράκταλ. Οι κανόνες υποδιαίρεσης έχουν χρησιμοποιηθεί στην αρχιτεκτονική, τη βιολογία και την επιστήμη των υπολογιστών, καθώς και στη μελέτη των υπερβολικών πολλαπλών. Τα πλακίδια αντικατάστασης είναι ένας καλά μελετημένος τύπος κανόνα υποδιαίρεσης.

Ορισμός

Ένας κανόνας υποδιαίρεσης χρησιμοποιεί ένα πλακίδιο του επιπέδου με πολύγωνα και το μετατρέπει σε ένα νέο πλακίδιο υποδιαιρώντας κάθε πολύγωνο σε μικρότερα πολύγωνα. Είναι πεπερασμένος αν υπάρχουν μόνο πεπερασμένοι τρόποι με τους οποίους κάθε πολύγωνο μπορεί να υποδιαιρεθεί. Κάθε τρόπος υποδιαίρεσης ενός πλακιδίου ονομάζεται τύπος πλακιδίου. Κάθε τύπος πλακιδίου αντιπροσωπεύεται από μια ετικέτα (συνήθως ένα γράμμα). Κάθε τύπος πλακιδίου υποδιαιρείται σε μικρότερους τύπους πλακιδίων. Κάθε ακμή υποδιαιρείται επίσης σύμφωνα με πεπερασμένα πολλά είδη ακμών. Οι πεπερασμένοι κανόνες υποδιαίρεσης μπορούν να υποδιαιρέσουν μόνο πλακίδια που αποτελούνται από πολύγωνα με ετικέτες από τύπους πλακιδίων. Τέτοια πλακίδια ονομάζονται σύμπλοκα υποδιαίρεσης για τον κανόνα υποδιαίρεσης. Δεδομένου οποιουδήποτε συμπλέγματος υποδιαίρεσης για έναν κανόνα υποδιαίρεσης, μπορούμε να το υποδιαιρέσουμε ξανά και ξανά για να πάρουμε μια ακολουθία από πλακίδια .

Παραδείγματος χάριν, η δυαδική υποδιαίρεση έχει έναν τύπο πλακιδίων και έναν τύπο ακμών:

Ο κανόνας δυαδικής υποδιαίρεσης

Δεδομένου ότι ο μόνος τύπος πλακιδίων είναι το τετράπλευρο, η δυαδική υποδιαίρεση μπορεί να υποδιαιρέσει μόνο πλακίδια που αποτελούνται από τετράπλευρα. Αυτό σημαίνει ότι τα μόνα σύμπλοκα υποδιαίρεσης είναι πλακοστρώσεις από τετράπλευρα. Το πλακίδιο μπορεί να είναι κανονικό, χωρίς όμως να είναι απαραίτητο:

Αρχίζουμε με ένα σύμπλεγμα με τέσσερα τετράπλευρα και υποδιαιρούμε δύο φορές. Όλα τα τετράγωνα είναι πλακίδια τύπου Α.

Εδώ ξεκινάμε με ένα σύμπλεγμα από τέσσερα τετράπλευρα και το υποδιαιρούμε δύο φορές. Όλα τα τετράπλευρα είναι πλακίδια τύπου Α.

Παραδείγματα κανόνων πεπερασμένης υποδιαίρεσης

Η βαρυκεντρική υποδιαίρεση είναι ένα παράδειγμα κανόνα υποδιαίρεσης με έναν τύπο ακμής (που υποδιαιρείται σε δύο ακμές) και έναν τύπο πλακιδίου (ένα τρίγωνο που υποδιαιρείται σε 6 μικρότερα τρίγωνα). Οποιαδήποτε τριγωνική επιφάνεια είναι ένα σύμπλεγμα βαρυκεντρικής υποδιαίρεσης.

Το πλακίδιο Πενρόζε μπορεί να παραχθεί από έναν κανόνα υποδιαίρεσης σε ένα σύνολο τεσσάρων τύπων πλακιδίων (οι καμπύλες γραμμές στον παρακάτω πίνακα βοηθούν μόνο να δείξουν πώς τα πλακίδια ταιριάζουν μεταξύ τους):

Όνομα	Αρχικά πλακίδια	Γενιά 1	Γενιά 2	Γενιά 3
Μισός χαρταετός
Μισό βέλος
Ήλιος
Αστέρι

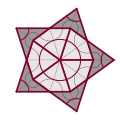
Ορισμένοι ορθολογικοί χάρτες οδηγούν σε κανόνες πεπερασμένης υποδιαίρεσης Αυτό περιλαμβάνει τους περισσότερους χάρτες Lattès.

Κάθε πρώτος, μη διαιρεμένος εναλλασσόμενος κόμβος ή συμπλήρωμα συνδέσμου έχει έναν κανόνα υποδιαίρεσης, με κάποια πλακίδια που δεν υποδιαιρούνται, που αντιστοιχούν στο όριο του συμπληρώματος συνδέσμου. Οι κανόνες υποδιαίρεσης δείχνουν πώς θα έμοιαζε ο νυχτερινός ουρανός σε κάποιον που ζει σε ένα συμπλήρωμα κόμβου- επειδή το σύμπαν τυλίγεται γύρω από τον εαυτό του (δηλαδή δεν είναι απλά συνδεδεμένο), ένας παρατηρητής θα έβλεπε το ορατό σύμπαν να επαναλαμβάνεται σε ένα άπειρο μοτίβο. Ο κανόνας υποδιαίρεσης περιγράφει αυτό το μοτίβο.

Ο κανόνας υποδιαίρεσης φαίνεται διαφορετικός για διαφορετικές γεωμετρίες. Αυτός είναι ένας κανόνας υποδιαίρεσης για τον τρίφυλλο κόμβο, ο οποίος δεν είναι υπερβολικός κόμβος:

Κανόνας υποδιαίρεσης του τριφυλλιού

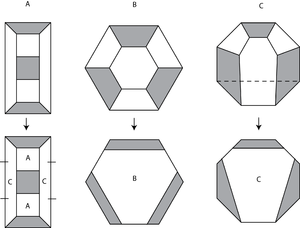
Και αυτός είναι ο κανόνας υποδιαίρεσης για τους δακτυλίους Borromean, ο οποίος είναι υπερβολικός:

Κανόνας υποδιαίρεσης Borromean

Σε κάθε περίπτωση, ο κανόνας υποδιαίρεσης ενεργεί σε κάποιο πλακίδιο της σφαίρας (π.χ. στον νυχτερινό ουρανό), αλλά είναι ευκολότερο να σχεδιάσουμε απλώς ένα μικρό μέρος του νυχτερινού ουρανού, που αντιστοιχεί σε ένα μόνο πλακίδιο που υποδιαιρείται επανειλημμένα. Αυτό συμβαίνει για τον κόμβο του τριφυλλιού:

Υποδιαιρέσεις του συμπλέγματος υποδιαιρέσεων για το συμπλήρωμα τριφυλλιού.

Και για τα δαχτυλίδια Borromean:

Υποδιαιρέσεις του συμπλέγματος υποδιαιρέσεων για το συμπλήρωμα των δακτυλίων Borromean.

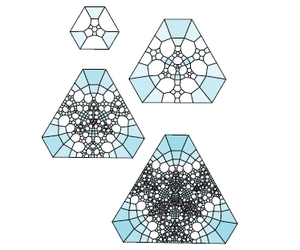
Κανόνες υποδιαίρεσης σε υψηλότερες διαστάσεις

Οι κανόνες υποδιαίρεσης μπορούν εύκολα να γενικευτούν σε άλλες διαστάσεις. Επίσης, η δυαδική υποδιαίρεση μπορεί να γενικευτεί σε άλλες διαστάσεις (όπου οι υπερκύβοι διαιρούνται από κάθε μεσαίο επίπεδο), όπως στην απόδειξη του θεωρήματος Χάινε- Μπορέλ.

Αυστηρός ορισμός

Ένας κανόνας υποδιαίρεσης για τον τετράτορο. Οι επιφάνειες των πλακιδίων B που υποδιαιρούνται μπορούν να αγγίζουν μόνο τα πλακίδια C, και οι επιφάνειες των πλακιδίων B που δεν αγγίζουν μόνο τα πλακίδια A.

Ένας κανόνας πεπερασμένης υποδιαίρεσης $R$ αποτελείται από τα εξής.

1. Ένα πεπερασμένο 2-διάστατο σύμπλεγμα CW $S_{R}$, το οποίο αποκαλείται σύμπλεγμα υποδιαίρεσης, με σταθερή δομή κελιών, έτσι ώστε το $S_{R}$ να είναι η ένωση των κλειστών 2 κελιών του. Υποθέτουμε ότι για κάθε κλειστό 2-κύτταρο ${\tilde {s}}$ του $S_{R}$ υπάρχει μια δομή CW $s$ σε ένα κλειστό 2-δίσκο έτσι ώστε το $s$ να έχει τουλάχιστον δύο κορυφές, οι κορυφές και οι ακμές του $s$ να περιέχονται στο $\partial s$, και ο χαρακτηριστικός χάρτης $\psi _{s}:s\rightarrow S_{R}$ που απεικονίζει πάνω στο ${\tilde {s}}$ περιορίζεται σε ομοιομορφισμό πάνω σε κάθε ανοικτό κελί.

2. Ένα πεπερασμένο δισδιάστατο σύμπλεγμα CW $R(S_{R})$, το οποίο αποτελεί υποδιαίρεση του $S_{R}$.

3.Ένας συνεχής κυψελοειδής χάρτης $\phi _{R}:R(S_{R})\rightarrow S_{R}$ που ονομάζεται χάρτης υποδιαίρεσης, του οποίου ο περιορισμός σε κάθε ανοιχτό κελί είναι ομοιομορφισμός σε ένα ανοιχτό κελί.

Κάθε σύμπλεγμα CW $s$ στον παραπάνω ορισμό (με τον δεδομένο χαρακτηριστικό του χάρτη $\psi _{s}$) ονομάζεται τύπος πλακιδίου.

Ένα σύμπλεγμα $R$ για έναν κανόνα υποδιαίρεσης $R$ είναι ένα 2-διάστατο σύμπλεγμα CW $X$ που είναι η ένωση των κλειστών 2 κελιών του, μαζί με έναν συνεχή κυτταρικό χάρτη $f:X\rightarrow S_{R}$ του οποίου ο περιορισμός σε κάθε ανοικτό κελί είναι ομοιομορφισμός. Μπορούμε να υποδιαιρέσουμε το $X$ σε ένα σύμπλεγμα $R(X)$ απαιτώντας ότι ο επαγόμενος χάρτης $f:R(X)\rightarrow R(S_{R})$ περιορίζεται σε ομοιομορφισμό σε κάθε ανοικτό κελί. Το $R(X)$ είναι πάλι ένα $R$-σύμπλεγμα με χάρτη $\phi _{R}\circ f:R(X)\rightarrow S_{R}$. Επαναλαμβάνοντας αυτή τη διαδικασία, λαμβάνουμε μια ακολουθία υποδιαιρεμένων $R$-συμπλεγμάτων $R^{n}(X)$ με χάρτες $\phi _{R}^{n}\circ f:R^{n}(X)\rightarrow S_{R}$.

Η δυαδική υποδιαίρεση είναι ένα παράδειγμα:

Ο κανόνας δυαδικής υποδιαίρεσης.

Το σύμπλεγμα υποδιαίρεσης μπορεί να δημιουργηθεί με τη συγκόλληση των απέναντι άκρων του τετραγώνου, μετατρέποντας το σύμπλεγμα υποδιαίρεσης $S_{R}$ σε τόρο. Ο χάρτης υποδιαίρεσης $\phi$ είναι ο χάρτης διπλασιασμού στον τόρο, τυλίγοντας τον μεσημβρινό γύρω από τον εαυτό του δύο φορές και το γεωγραφικό μήκος γύρω από τον εαυτό του δύο φορές. Πρόκειται για έναν χάρτη τετραπλής κάλυψης. Το επίπεδο, πλακοστρωμένο με τετράγωνα, είναι ένα σύμπλεγμα υποδιαίρεσης για αυτόν τον κανόνα υποδιαίρεσης, με τον χάρτη δομής $f:\mathbb {R} ^{2}\rightarrow R(S_{R})$ που δίνεται από τον τυπικό χάρτη κάλυψης. Με την υποδιαίρεση, κάθε τετράγωνο στο επίπεδο υποδιαιρείται σε τετράγωνα του ενός τετάρτου του μεγέθους.

Ιδιότητες οιονεί ισομετρίας

Το ιστορικό γράφημα του κανόνα υποδιαίρεσης των μεσαίων τρίτων

Οι κανόνες υποδιαίρεσης μπορούν να χρησιμοποιηθούν για τη μελέτη των οιονεί ισομετρικών ιδιοτήτων ορισμένων χώρων. Με δεδομένο έναν κανόνα υποδιαίρεσης $R$ και ένα σύμπλεγμα υποδιαίρεσης $X$, µπορούµε να κατασκευάσουµε ένα γράφηµα που ονοµάζεται ιστορικό γράφηµα και καταγράφει τη δράση του κανόνα υποδιαίρεσης. Αυτός ο γράφος αποτελείται από τους διπλούς γράφους κάθε βήματος $R^{n}(X)$, και τις άκρες που συνδέουν κάθε πλακίδιο στο $R^{n}(X)$ με τις υποδιαιρέσεις του στο $R^{n+1}(X)$.

Οι ιδιότητες οιονεί ισομετρίας του γραφήματος ιστορίας μπορούν να μελετηθούν με τη χρήση κανόνων υποδιαίρεσης. Παραδείγματος χάριν, ο γράφος ιστορίας είναι οιονεί ισομετρικός με τον υπερβολικό χώρο ακριβώς όταν ο κανόνας υποδιαίρεσης είναι σύμμορφος, όπως περιγράφεται στο συνδυαστικό θεώρημα απεικόνισης του Ρίμαν.

Εφαρμογές

Εφαρμογές των κανόνων υποδιαίρεσης.

Ένα παράδειγμα ενός κανόνα υποδιαίρεσης που χρησιμοποιείται στην ισλαμική τέχνη γνωστή ως girih..

Τα τρία πρώτα βήματα της υποδιαίρεσης Catmull-Clark ενός κύβου με την επιφάνεια υποδιαίρεσης από κάτω.

Η φύση της διακλάδωσης των βρόγχων μπορεί να διαμορφωθεί με κανόνες πεπερασμένης υποδιαίρεσης.

Τα κεραμίδια Girih της ισλαμικής αρχιτεκτονικής είναι αυτοομοειδή κεραμίδια που μπορούν να διαμορφωθούν με πεπερασμένους κανόνες υποδιαίρεσης. Το 2007, ο Πίτερ Τζ. Λου του Πανεπιστημίου Χάρβαρντ και ο καθηγητής Πολ Τζ. Στάινχαρντ του Πανεπιστημίου Πρίνστον δημοσίευσαν μια εργασία στο περιοδικό Science, στην οποία προτείνουν ότι τα κεραμίδια Girih διαθέτουν ιδιότητες συμβατές με τα αυτο-ομοειδή οιονεί κρυσταλλικά μορφοκλασματικά κεραμίδια, όπως τα κεραμίδια Penrose (παρουσίαση 1974, προγενέστερες εργασίες που ξεκίνησαν γύρω στο 1964), τα οποία προηγούνται κατά πέντε αιώνες .

Οι επιφάνειες υποδιαίρεσης στα γραφικά υπολογιστών χρησιμοποιούν κανόνες υποδιαίρεσης για να βελτιώσουν μια επιφάνεια σε ένα δεδομένο επίπεδο ακρίβειας. Αυτές οι επιφάνειες υποδιαίρεσης (όπως η επιφάνεια υποδιαίρεσης Catmull-Clark) παίρνουν ένα πλέγμα πολυγώνων (ο τύπος που χρησιμοποιείται στις τρισδιάστατες ταινίες κινουμένων σχεδίων) και το βελτιώνουν σε ένα πλέγμα με περισσότερα πολύγωνα προσθέτοντας και μετακινώντας σημεία σύμφωνα με διάφορους αναδρομικούς τύπους. Αν και πολλά σημεία μετακινούνται κατά τη διαδικασία αυτή, κάθε νέο πλέγμα είναι, από συνδυαστική άποψη, μια υποδιαίρεση του παλιού πλέγματος (πράγμα που σημαίνει ότι για κάθε ακμή και κορυφή στο παλιό πλέγμα, μπορείτε να προσδιορίσετε μια αντίστοιχη ακμή και κορυφή στο νέο πλέγμα, καθώς και αρκετές άλλες άκρες και κορυφές).

Οι κανόνες υποδιαίρεσης εφαρμόστηκαν από τους Cannon, Floyd και Parry (2000) στη μελέτη των μοτίβων ανάπτυξης μεγάλης κλίμακας των βιολογικών οργανισμών. Οι Cannon, Floyd και Parry ανέπτυξαν ένα μαθηματικό πρότυπο ανάπτυξης το οποίο έδειξε ότι ορισμένα συστήματα που καθορίζονται από απλούς πεπερασμένους κανόνες υποδιαίρεσης μπορούν να οδηγήσουν σε αντικείμενα (στο παράδειγμά τους, έναν κορμό δέντρου) των οποίων η μορφή μεγάλης κλίμακας ταλαντώνεται άγρια με την πάροδο του χρόνου, παρόλο που οι τοπικοί νόμοι υποδιαίρεσης παραμένουν οι ίδιοι. Οι Cannon, Floyd και Parry εφάρμοσαν επίσης το μοντέλο τους στην ανάλυση των προτύπων ανάπτυξης των ιστών αρουραίων. Πρότειναν ότι η "αρνητικά καμπυλωτή" (ή μη ευκλείδεια) φύση των μικροσκοπικών προτύπων ανάπτυξης των βιολογικών οργανισμών είναι ένας από τους βασικούς λόγους για τους οποίους οι οργανισμοί μεγάλης κλίμακας δεν μοιάζουν με κρυστάλλους ή πολυεδρικά σχήματα αλλά στην πραγματικότητα σε πολλές περιπτώσεις μοιάζουν με αυτοομοιόμορφα φράκταλ. Ειδικότερα, πρότειναν ότι μια τέτοια "αρνητικά καμπυλωτή" τοπική δομή εκδηλώνεται στην ιδιαίτερα διπλωμένη και ιδιαίτερα συνδεδεμένη φύση του εγκεφάλου και του πνευμονικού ιστού.

Η εικασία Cannon

Οι Cannon, Floyd και Parry μελέτησαν για πρώτη φορά τους κανόνες πεπερασμένης υποδιαίρεσης σε μια προσπάθεια να αποδείξουν την ακόλουθη εικασία:

Η εικασία Cannon: Κάθε υπερβολική ομάδα Γκρόμοφ με μια 2-σφαίρα στο άπειρο δρα γεωμετρικά στον υπερβολικό 3-χώρο.

Εδώ, μια γεωμετρική δράση είναι μια συμπαγής, κατάλληλα ασυνεχής δράση με ισομετρίες. Αυτή η εικασία λύθηκε εν μέρει από τον Γκριγκόρι Πέρελμαν (Grigory Perelman) στην απόδειξη της εικασίας της γεωμετρίας, η οποία δηλώνει (εν μέρει) ότι κάθε υπερβολική ομάδα Γκρόμοφ που είναι ομάδα 3-πολλαπλοτήτων πρέπει να δρα γεωμετρικά στον υπερβολικό 3-χώρο. Ωστόσο, απομένει ακόμη να αποδειχθεί ότι μια υπερβολική ομάδα Γκρόμοφ με 2 σφαίρες στο άπειρο είναι μια ομάδα 3-πολλαπλοτήτων.

Οι Cannon και Σουένσον έδειξαν ότι μια υπερβολική ομάδα με μια 2-σφαίρα στο άπειρο έχει έναν σχετικό κανόνα υποδιαίρεσης. Αν αυτός ο κανόνας υποδιαίρεσης είναι σύμμορφος με μια ορισμένη έννοια, η ομάδα θα είναι μια ομάδα 3-πολλαπλών με τη γεωμετρία του υπερβολικού 3-χώρου .

Συνδυαστικό θεώρημα απεικόνισης Ρίμαν

Οι κανόνες υποδιαίρεσης δίνουν μια ακολουθία από πλακίδια μιας επιφάνειας, και τα πλακίδια δίνουν μια ιδέα της απόστασης, του μήκους και του εμβαδού (αφήνοντας κάθε πλακίδιο να έχει μήκος και εμβαδόν 1). Στο όριο, οι αποστάσεις που προκύπτουν από αυτά τα πλακίδια μπορεί να συγκλίνουν κατά κάποιο τρόπο σε μια αναλυτική δομή στην επιφάνεια. Το Συνδυαστικό Θεώρημα Χαρτογράφησης Ρίμαν δίνει αναγκαίες και ικανές συνθήκες για να συμβεί αυτό.

Η διατύπωσή της χρειάζεται κάποιο υπόβαθρο. Ένα πλακίδιο $T$ ενός δακτυλίου $R$ (δηλαδή, ένας κλειστός δακτύλιος) δίνει δύο αναλλοίωτες, $M_{\sup }(R,T)$ και $m_{\inf }(R,T)$, που ονομάζονται προσεγγιστικά moduli. Αυτά είναι παρόμοια με τα κλασικά modulus ενός δακτυλίου. Ορίζονται με τη χρήση συναρτήσεων βάρους. Μια συνάρτηση βάρους $\rho$ αναθέτει έναν μη αρνητικό αριθμό που ονομάζεται βάρος σε κάθε πλακίδιο του $T$. Σε κάθε μονοπάτι στο $R$ μπορεί να δοθεί ένα μήκος, που ορίζεται ως το άθροισμα των βαρών όλων των πλακιδίων στο μονοπάτι. Ορίζουμε το ύψος $H(\rho )$ του $R$ υπό $\rho$ ως το infimum του μήκους όλων των πιθανών μονοπατιών που συνδέουν το εσωτερικό όριο του $R$ με το εξωτερικό όριο. Η περίμετρος $C(\rho )$ του $R$ υπό $\rho$ είναι το infimum του μήκους όλων των δυνατών μονοπατιών που κυκλώνουν τον δακτύλιο (δηλαδή δεν είναι μηδενικά ομοιογενή στο R). Το εμβαδόν $A(\rho )$ του $R$ υπό $\rho$ ορίζεται ως το άθροισμα των τετραγώνων όλων των βαρών στο $R$ . Στη συνέχεια, ορίζουμε ότι

$M_{\sup }(R,T)=\sup {\frac {H(\rho )^{2}}{A(\rho )}},$

$m_{\inf }(R,T)=\inf {\frac {A(\rho )}{C(\rho )^{2}}}.$

Να σημειωθεί ότι είναι αναλλοίωτες σε αλλαγές στην κλίμακα της μετρικής.

Μια ακολουθία $T_{1},T_{2},\ldots$ από πλακίδια είναι σύμμορφη ($K$) αν το πλέγμα πλησιάζει το 0 και:

1. Για κάθε δακτύλιο $R$, τα προσεγγιστικά moduli $M_{\sup }(R,T_{i})$ και $m_{\inf }(R,T_{i})$, για όλα τα $i$ επαρκώς μεγάλα, βρίσκονται σε ένα ενιαίο διάστημα της μορφής $[r,Kr]$και
2. Δίνεται ένα σημείο $x$ i στην επιφάνεια, μια γειτονιά $N$ του $x$ και ένας ακέραιος $I$, υπάρχει ένας δακτύλιος $R$ στο $N\smallsetminus \{x\}$ που διαχωρίζει το x από το συμπλήρωμα του $N$, έτσι ώστε για όλα τα μεγάλα $i$ τα προσεγγιστικά moduli του $R$ να είναι όλα μεγαλύτερα από το $I$.

Δήλωση θεωρήματος

Αν μια ακολουθία $T_{1},T_{2},\ldots$ από πλακίδια μιας επιφάνειας είναι σύμμορφη ($K$) με την παραπάνω έννοια, τότε υπάρχει μια σύμμορφη δομή στην επιφάνεια και μια σταθερά $K'$ που εξαρτάται μόνο από την $K$ στην οποία οι κλασσικές και οι προσεγγιστικές μοντούλες (από την $T_{i}$ για $i$ αρκετά μεγάλο) οποιουδήποτε δεδομένου δακτυλίου είναι $K'$-συγκρίσιμες, που σημαίνει ότι βρίσκονται σε ένα ενιαίο διάστημα $[r,K'r]$.

Συνέπειες

Το Θεώρημα Συνδυαστικής Απεικόνισης Ρίμαν υποδηλώνει ότι μια ομάδα $G$ δρα γεωμετρικά στην $\mathbb {H} ^{3}$ αν και μόνο αν είναι υπερβολική κατά Gromov, έχει μια σφαίρα στο άπειρο και ο φυσικός κανόνας υποδιαίρεσης στη σφαίρα οδηγεί σε μια ακολουθία πλακοστρώσεων που είναι σύμμορφη με την παραπάνω έννοια. Έτσι, η εικασία Cannon θα ήταν αληθής αν όλοι αυτοί οι κανόνες υποδιαίρεσης ήταν σύμμορφοι.

Εξωτερικός σύνδεσμος

• Bill Floyd's research page. This page contains most of the research papers by Cannon, Floyd and Parry on subdivision rules, as well as a gallery of subdivision rules.

Δείτε επίσης

• Αλγόριθμος διαμαντιού τετραγώνου
• Καμπύλη που γεμίζει το χώρο
• Νιφάδα του Κοχ
• Καμπύλη Χίλμπερτ
• Καμπύλη του δράκου
• Σπόγγος του Μένγκερ

• Σύνολο Μάντελμπροτ
• Σύνολο Julia
• Οικοδομήσιμο Σύμπαν