Κλειστό σύστημα
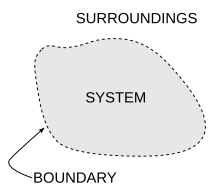
Ένα κλειστό σύστημα είναι ένα φυσικό σύστημα (physical system) που δεν επιτρέπει συγκεκριμένους τύπους μεταφοράς (όπως μεταφορά μάζας) μέσα ή έξω από το σύστημα. Η προδιαγραφή του, ποιοι τύποι μεταφοράς αποκλείονται, ποικίλει στα κλειστά συστήματα της φυσικής, της χημείας ή της μηχανικής.
Στη φυσική[Επεξεργασία | επεξεργασία κώδικα]
Στην κλασσική μηχανική[Επεξεργασία | επεξεργασία κώδικα]
Στη μη σχετιστική (nonrelativistic) κλασική μηχανική, ένα κλειστό σύστημα είναι ένα φυσικό σύστημα που δεν ανταλλάσσει οποιαδήποτε ύλη με το περιβάλλον του και δεν υπόκειται σε καμιά δύναμη της οποίας η προέλευση είναι εξωτερική ως προς το σύστημα.[1][2] Ένα κλειστό σύστημα στην κλασική μηχανική μπορεί να θεωρηθεί ένα απομονωμένο σύστημα (isolated system) στη θερμοδυναμική.
Στη θερμοδυναμική[Επεξεργασία | επεξεργασία κώδικα]
Στη θερμοδυναμική, ένα κλειστό σύστημα μπορεί να ανταλλάξει ενέργεια (ως θερμότητα ή έργο (φυσική)), αλλά όχι ως ύλη, με το περιβάλλον του. Ένα απομονωμένο σύστημα δεν μπορεί να ανταλλάξει οποιαδήποτε θερμότητα, έργο, ή ύλη με το περιβάλλον, ενώ ένα ανοικτό σύστημα μπορεί να ανταλλάξει ενέργεια και ύλη. [3][4][5][6][7][8][9] (Αυτό το σχήμα ορισμού των όρων δεν χρησιμοποιείται ομοιόμορφα, αν και είναι βολικό για κάποιους σκοπούς. Ειδικά, κάποιοι συγγραφείς χρησιμοποιούν τον όρο 'κλειστό σύστημα' αντί του εδώ χρησιμοποιούμενου όρου 'απομονωμένο σύστημα'.[10][11]) Για ένα απλό σύστημα, με έναν μόνο τύπο σωματιδίων (άτομα ή μόρια), ένα κλειστό σύστημα ισοδυναμεί με έναν σταθερό αριθμό σωματιδίων. Όμως, για συστήματα που βρίσκονται σε χημική αντίδραση, μπορούν να δημιουργούνται και να καταστρέφονται όλα τα είδη από τη διεργασία της αντίδρασης. Σε αυτήν την περίπτωση, το γεγονός ότι το σύστημα είναι κλειστό, εκφράζεται δηλώνοντας ότι ο συνολικός αριθμός κάθε στοιχειακού ατόμου διατηρείται, ανεξάρτητα από το είδος του μορίου στο οποίο μπορεί να ανήκει. Μαθηματικά:
όπου είναι ο αριθμός των μορίων τύπου j, είναι ο αριθμός των ατόμων του στοιχείου i στο μόριο j και bi είναι ο συνολικός αριθμός των ατόμων του στοιχείου i στο σύστημα, που παραμένει σταθερό, επειδή το σύστημα είναι κλειστό. Θα υπάρχει μια τέτοια εξίσωση για κάθε διαφορετικό στοιχείο στο σύστημα.
Στη χημεία[Επεξεργασία | επεξεργασία κώδικα]
Στη χημεία, ένα κλειστό σύστημα είναι ένα σύστημα όπου κανένα αντιδρόν ή προϊόν δεν μπορεί να διαφύγει.
Στη μηχανική[Επεξεργασία | επεξεργασία κώδικα]
Σε ένα περιεχόμενο επιστημών μηχανικών (engineering), ένα κλειστό σύστημα είναι ένα δεσμευμένο σύστημα, δηλαδή καθορισμένο, στο οποίο κάθε εισαγωγή είναι γνωστή και κάθε συνισταμένη είναι γνωστή (ή μπορεί να είναι γνωστή) μέσα σε έναν συγκεκριμένο χρόνο.
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Rana, N.C.· P.S. Joag (1991). Classical Mechanics. σελ. 78. ISBN 978-0-07-460315-4.
- ↑ Landau, L.D.· E.M. Lifshitz (1976). Mechanics (third έκδοση). σελ. 8. ISBN 978-0-7506-2896-9.
- ↑ Prigogine, I., Defay, R. (1950/1954). Chemical Thermodynamics, Longmans, Green & Co, London, p. 66.
- ↑ Tisza, L. (1966). Generalized Thermodynamics, M.I.T Press, Cambridge MA, pp. 112–113.
- ↑ Guggenheim, E.A. (1949/1967). Thermodynamics. An Advanced Treatment for Chemists and Physicists, (1st edition 1949) 5th edition 1967, North-Holland, Amsterdam, p. 14.
- ↑ Münster, A. (1970). Classical Thermodynamics, translated by E.S. Halberstadt, Wiley–Interscience, London, pp. 6–7.
- ↑ Haase, R. (1971). Survey of Fundamental Laws, chapter 1 of Thermodynamics, pages 1–97 of volume 1, ed. W. Jost, of Physical Chemistry. An Advanced Treatise, ed. H. Eyring, D. Henderson, W. Jost, Academic Press, New York, lcn 73–117081, p. 3.
- ↑ Tschoegl, N.W. (2000). Fundamentals of Equilibrium and Steady-State Thermodynamics, Elsevier, Amsterdam, ISBN 0-444-50426-5, p. 5.
- ↑ Silbey, R.J., Alberty, R.A., Bawendi, M.G. (1955/2005). Physical Chemistry, fourth edition, Wiley, Hoboken NJ, p. 4.
- ↑ Callen, H.B. (1960/1985). Thermodynamics and an Introduction to Thermostatistics, (1st edition 1960) 2nd edition 1985, Wiley, New York, ISBN 0-471-86256-8, p. 17.
- ↑ ter Haar, D., Wergeland, H. (1966). Elements of Thermodynamics, Addison-Wesley Publishing, Reading MA, p. 43.



