Αυξητικά υλικά
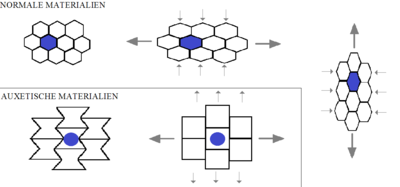
Αυξητικά υλικά, απλώς αυξητικά (αγγλ. Auxetics, Auxetic structures) είναι δομές ή υλικά τα οποία έχουν αρνητικό λόγο Poisson.[1]
Αρνητικό λόγος Poisson
[Επεξεργασία | επεξεργασία κώδικα]Ο λόγος αυτός, στην επιστήμη των υλικών αλλά και στη μηχανική, είναι ένα μέτρο του φαινομένου Poisson, δηλ. όταν τα υλικά αυτά επιμηκύνονται δηλ. τεντώνονται, γίνονται παχύτερα κάθετα στην εφαρμοζόμενη δύναμη. Αυτό συμβαίνει λόγω της ιδιαίτερης εσωτερικής τους δομής και του τρόπου παραμόρφωσης όταν το δείγμα φορτίζεται σε έναν μόνο άξονα (μονοαξονικά). Μπορεί επίσης να παραμένουν μορφολογικά ίδια (κάθετα δηλαδή στη φόρτιση). Αυτό συμβαίνει εξαιτίας της ιδιαίτερης μορφής τους (βλ. κυψέλες - honeycombs) ή της εσωτερικής σύστασής τους.

Τι είναι;
[Επεξεργασία | επεξεργασία κώδικα]Τα αυξητικά υλικά μπορεί να είναι απλά μόρια, ή κρυσταλλικά ή να είναι συνήθως χημικές δομές από μακρομόρια. Μπορεί να έχουν εφαρμογές σε εξειδικευμένες χρήσεις[2], όπως αλεξίσφαιρα γιλέκα, υλικά αποθήκευσης ή στοίβαξης, απορροφητικά υλικά, ειδικά αθλητικά είδη (προφύλαξης), πολύστρωτα σύνθετα, κ.α.[3]
Προέλευση όρου
[Επεξεργασία | επεξεργασία κώδικα]Ο διεθνής τεχνικός όρος, Auxetics, προέρχεται από την ελληνική λέξη «αὐξητικός» (auxetikos) και καθιερώθηκε το 1996 από τον καθηγητή Ken Evans του Πανεπιστημίου Exeter.[4][5]
Παραδείγματα
[Επεξεργασία | επεξεργασία κώδικα]Ορισμένα παραδείγματα αυξητικών υλικών, συμπεριλαμβάνουν:
- Αφρός αυξητικής πολυουρεθάνης[6][7]
- Χριστοβαλίτης (Cristobalite) [8]
- Πολυμερή υγρής κρυστάλλωσης[9]
- Κρυσταλλικά υλικά με βάση: Li, Na, K, Cu, Rb, Ag, Fe, Ni, Co, Cs, Au, Be, Ca, Zn, Sr, Sb, MoS, BAsO[10][11][12]
- Ορισμένα πετρώματα και ορυκτά[13]
- Γραφένιο[14][15]
- Μη ανθρακούχοι νανοσωλήνες[16][17]
- Ιστοί ορισμένων οστών
- Τένοντες[18]
- Πολυμερή τύπου Gore-Tex[19]
- Χαρτί (ορισμένου τύπου)[20][21]
- Οριγκάμι (ήτοι, Ιαπωνία καλλιτεχνία διπλώματος χαρτιού)[22][23] and other periodic patterns derived from it.[24][25]
- Τεχνητές δομές με μηδενικό Poisson's ratio.[26][27][28][29][30][31]
- Ορισμένα υφαντά[32][33]
- Φελλός.
Παραπομπές
[Επεξεργασία | επεξεργασία κώδικα]- ↑ https://www.hindawi.com/journals/amse/2014/753496/
- ↑ «Hook's law». The Economist. 1 December 2012. https://www.economist.com/news/technology-quarterly/21567203-materials-auxetic-substances-which-get-fatter-rather-thinner-when-stretched. Ανακτήθηκε στις 1 March 2013.
- ↑ https://hellanicus.lib.aegean.gr/handle/11610/9062
- ↑ Quinion, Michael (9 November 1996), Auxetic, http://www.worldwidewords.org/turnsofphrase/tp-aux1.htm.
- ↑ Evans, Ken (1991), «Auxetic polymers: a new range of materials.», Endeavour 15 (4): 170–174, doi:.
- ↑ Li, Yan; Zeng, Changchun (2016). «On the successful fabrication of auxetic polyurethane foams: Materials requirement, processing strategy and conversion mechanism». Polymer 87: 98–107. doi:.
- ↑ Li, Yan; Zeng, Changchun (2016). «Room‐Temperature, Near‐Instantaneous Fabrication of Auxetic Materials with Constant Poisson's Ratio over Large Deformation». Advanced Materials 28 (14): 2822–2826. doi:. PMID 26861805.
- ↑ Yeganeh-Haeri, Amir; Weidner, Donald J.; Parise, John B. (31 July 1992). «Elasticity of α-Cristobalite: A Silicon Dioxide with a Negative Poisson's Ratio» (στα αγγλικά). Science 257 (5070): 650–652. doi:. ISSN 0036-8075. PMID 17740733. Bibcode: 1992Sci...257..650Y. https://archive.org/details/sim_science_1992-07-31_257_5070/page/650.
- ↑ Verma, Prateek; He, Chaobin; Griffin, Anselm C. (23 August 2020). «Implications for Auxetic Response in Liquid Crystalline Polymers: X‐Ray Scattering and Space‐Filling Molecular Modeling». physica status solidi (b): 2000261. doi:.
- ↑ Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S. (2013). «Classification of cubic auxetics» (στα αγγλικά). Physica Status Solidi B 250 (10): 2038–2043. doi:.
- ↑ Gorodtsov, V.A.; Lisovenko, D.S. (2019). «Extreme values of Young's modulus and Poisson's ratio of hexagonal crystals» (στα αγγλικά). Mechanics of Materials 134: 1–8. doi:.
- ↑ Grima-Cornish, JN; Vella-Zarb, L; Grima, JN (2020). «Negative Linear Compressibility and Auxeticity in Boron Arsenate». Annalen der Physik 532 (5): 1900550. doi:. Bibcode: 2020AnP...53200550G.
- ↑ Burke, Maria (7 June 1997), «A stretch of the imagination», New Scientist 154 (2085): 36, https://www.newscientist.com/article/mg15420854.200-a-stretch-of-the-imagination.html
- ↑ Grima, J. N.; Winczewski, S.; Mizzi, L.; Grech, M. C.; Cauchi, R.; Gatt, R.; Attard, D.; Wojciechowski, K.W. και άλλοι. (2014). «Tailoring Graphene to Achieve Negative Poisson's Ratio Properties». Advanced Materials 27 (8): 1455–1459. doi:. PMID 25504060.
- ↑ Grima, Joseph N.; Grech, Michael C.; Grima‐Cornish, James N.; Gatt, Ruben; Attard, Daphne (2018). «Giant Auxetic Behaviour in Engineered Graphene» (στα αγγλικά). Annalen der Physik 530 (6): 1700330. doi:. ISSN 1521-3889. Bibcode: 2018AnP...53000330G.
- ↑ Goldstein, R.V.; Gorodtsov, V.A.; Lisovenko, D.S.; Volkov, M.A. (2014). «Negative Poisson's ratio for cubic crystals and nano/microtubes» (στα αγγλικά). Physical Mesomechanics 17 (2): 97–115. doi:.
- ↑ Bryukhanov, I.A.; Gorodtsov, V.A.; Lisovenko, D.S. (2019). «Chiral Fe nanotubes with both negative Poisson's ratio and Poynting's effect. Atomistic simulation» (στα αγγλικά). Journal of Physics: Condensed Matter 31 (47): 475304. doi:. PMID 31398716. Bibcode: 2019JPCM...31U5304B.
- ↑ «Negative Poisson's ratios in tendons: An unexpected mechanical response». Acta Biomater. 24: 201–208. 2015. doi:. PMID 26102335. http://eprints.staffs.ac.uk/3517/1/AA_Negative_Possionsratio_Paper_M.pdf.
- ↑ Auxetic materials, 9 March 2001, http://www.azom.com/details.asp?ArticleID=168.
- ↑ Baum et al. 1984, Tappi journal, Öhrn, O. E. (1965): Thickness variations of paper on stretching, Svensk Papperstidn. 68(5), 141.
- ↑ Verma, Prateek; Shofner, ML; Griffin, AC (2013). «Deconstructing the auxetic behavior of paper». Physica Status Solidi B 251 (2): 289–296. doi:. Bibcode: 2014PSSBR.251..289V.
- ↑ Mark, Schenk (2011). Folded Shell Structures, PhD Thesis (PDF). University of Cambridge, Clare College.
- ↑ Lv, Cheng; Krishnaraju, Deepakshyam; Konjevod, Goran; Yu, Hongyu; Jiang, Hanqing (2015). «Origami based Mechanical Metamaterials». Scientific Reports 4: 5979. doi:. PMID 25099402.
- ↑ Eidini, Maryam; Paulino, Glaucio H. (2015). «Unraveling metamaterial properties in zigzag-base folded sheets». Science Advances 1 (8): e1500224. doi:. ISSN 2375-2548. PMID 26601253. Bibcode: 2015SciA....1E0224E.
- ↑ Eidini, Maryam (2016). «Zigzag-base folded sheet cellular mechanical metamaterials». Extreme Mechanics Letters 6: 96–102. doi:.
- ↑ Tiemo Bückmann (May 2012). «Tailored 3D Mechanical Metamaterials Made by Dip-in Direct-Laser-Writing Optical Lithography». Advanced Materials 24 (20): 2710–2714. doi:. PMID 22495906.
- ↑ Grima‐Cornish, James N.; Grima, Joseph N.; Evans, Kenneth E. (2017). «On the Structural and Mechanical Properties of Poly(Phenylacetylene) Truss-Like Hexagonal Hierarchical Nanonetworks» (στα αγγλικά). Physica Status Solidi B 254 (12): 1700190. doi:. ISSN 1521-3951. Bibcode: 2017PSSBR.25400190G.
- ↑ Cabras, Luigi; Brun, Michele (2014). «Auxetic two-dimensional lattices with Poisson's ratio arbitrarily close to −1» (στα αγγλικά). Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences 470 (2172): 20140538. doi:. ISSN 1364-5021. Bibcode: 2014RSPSA.47040538C.
- ↑ Carta, Giorgio; Brun, Michele; Baldi, Antonio (2016). «Design of a porous material with isotropic negative Poisson's ratio» (στα αγγλικά). Mechanics of Materials 97: 67–75. doi:.
- ↑ Cabras, Luigi; Brun, Michele (2016). «A class of auxetic three-dimensional lattices» (στα αγγλικά). Journal of the Mechanics and Physics of Solids 91: 56–72. doi:. Bibcode: 2016JMPSo..91...56C.
- ↑ Kaminakis, N; Stavroulakis, G (2012). «Topology optimization for compliant mechanisms, using evolutionary-hybrid algorithms and application to the design of auxetic materials». Composites Part B Engineering 43 (6): 2655–2668. doi:.
- ↑ Verma, Prateek; Lin, A; Wagner, KB; Shofner, ML; Griffin, AC (2015). «Inducing out-of-plane auxetic behavior in needle-punched nonwovens». Physica Status Solidi B 252 (7): 1455–1464. doi:. Bibcode: 2015PSSBR.252.1455V.
- ↑ Verma, Prateek; Shofner, Meisha L.; Lin, Angela; Wagner, Karla B.; Griffin, Anselm C. (2016). «Induction of auxetic response in needle-punched nonwovens: Effects of temperature, pressure, and time» (στα αγγλικά). Physica Status Solidi B 253 (7): 1270–1278. doi:. ISSN 1521-3951. Bibcode: 2016PSSBR.253.1270V.


