Παλινδρόμηση (στατιστική)
Η παλινδρόμηση είναι μια ευρέως χρησιμοποιούμενη στατιστική τεχνική μοντελοποίησης για την έρευνα της συσχέτισης μεταξύ μίας εξαρτώμενης μεταβλητής και μιας ή περισσότερων ανεξάρτητων μεταβλητών [1]. Χρησιμοποιείται με σκοπό την εκχώρηση δεδομένων σε μία πραγματική μεταβλητή πρόβλεψης[2], όπως ισχύει και στην περίπτωση της κατηγοριοποίησης όταν είναι διακριτή, αλλιώς καλείται παλινδρόμηση αν η μεταβλητή είναι συνεχής[3].Η παλινδρόμηση προϋποθέτει ότι τα σχετικά δεδομένα ταιριάζουν με μερικά γνωστά είδη συνάρτησης και μετά καθορίζει την καλύτερη συνάρτηση αυτού του είδους που μοντελοποιεί τα δεδομένα που έχουν δοθεί[4]. Αποτέλεσμα της παλινδρόμησης όταν χρησιμοποιείται ως τεχνική εξόρυξης δεδομένων, αποτελεί ένα μοντέλο που χρησιμοποιείται αργότερα για να προβλέψει τις τιμές της κατηγορίας για τα νέα δεδομένα. Τέτοια παραδείγματα εφαρμογής της παλινδρόμησης αποτελεί η πρόβλεψη της ζήτησης για ένα νέο προϊόν ή υπηρεσία συναρτήσει των δαπανών διαφήμισης ή ο υπολογισμός της ταχύτητας του ανέμου σε σχέση με την θερμοκρασία, την υγρασία και την ατμοσφαιρική πίεση του περιβάλλοντος.
Ιστορία[Επεξεργασία | επεξεργασία κώδικα]
Η στατιστική εμφανίστηκε, με την μορφή που την γνωρίζουμε σήμερα, τον 17ο αιώνα. Κατά την εξέλιξή της ανά τους αιώνες προέκυψαν διάφορες χρήσεις της λέξης "στατιστικής". Πολλοί ταυτίζουν τον όρο στατιστική με την καταγραφή δεδομένων διοίκησης που καταλήγουν σε μη αμφισβητήσιμους αριθμούς για την καλύτερη δυνατή εξαγωγή αποτελεσμάτων. Για άλλους είναι ένας κλάδος που διδάσκεται στο πανεπιστήμιο και χρησιμοποιείται σε άλλους επιστημονικούς κλάδους, όπως την ιατρική, την βιολογία, την οικονομία κ.ο.κ. Αυτό που αποτέλεσε κομβικό σημείο στην εξέλιξη της Στατιστικής, είναι η εισαγωγή, η εφαρμογή και η αξιοποίηση των εννοιών της μέσης τιμής, της διακύμανσης, της παλινδρόμησης και της συσχέτισης[5]. Ο Galton παρατηρεί ότι: «είναι δύσκολο να καταλάβει κανείς γιατί οι στατιστικοί απέκτησαν τη συνήθεια να περιορίζουν τις έρευνές τους στις μέσες τιμές και δεν ικανοποιούνται περισσότερο από μια ευρύτερη προοπτική. Φαίνεται να αγνοούν τα θέλγητρα της ποικιλίας». δεν εμπιστευόταν τις μέσες τιμές και στα πλαίσια των ευγονικών του ενασχολήσεων ενδιαφερόταν για τις διαφορές μεταξύ των όντων, άρα και τις αποκλίσεις από τη μέση τιμή. Σε αντιδιαστολή με το νόμο της κανονικής κατανομής χρησιμοποιεί αυτό που ονομάζει «νόμο των παρεκκλίσεων από τη μέση τιμή». Οι εργασίες του Galton καταλήγουν σε μια ανακάλυψη που καταστρέφει το σχήμα του Quetelet: μια κανονική κατανομή αντί να είναι ένδειξη ομοιογένειας, μπορεί να προκύπτει ως συνιστώσα πολλών διαφορετικών κατανομών που αντιστοιχούν σε επιμέρους πληθυσμούς με μέσες τιμές πολύ διαφορετικές μεταξύ τους. Έτσι, η μέση τιμή μιας κανονικής κατανομής γίνεται ένα κινούμενο κέντρο βάρους που εξαρτάται από τη σύνθεση των εσωτερικών δυνάμεων των κοινωνιών. Η διαπίστωση αυτή οδηγεί τον Galton στην ανακάλυψη της παλινδρόμησης[5].
Μοντέλα Παλινδρόμησης[Επεξεργασία | επεξεργασία κώδικα]
Όπως αναφέραμε και στην αρχή η Παλινδρόµηση (Regression) είναι µια στατιστική τεχνική µοντελοποίησης για την έρευνα της συσχέτισης µεταξύ µίας εξαρτώµενης µεταβλητής και µιας ή περισσότερων ανεξάρτητων μεταβλητών.Το Γενικευµένο Νευρωνικό ∆ίκτυο Παλινδρόµησης (Generalized Regression Neural Network -GRNN) µπορεί να εκτελέσει διεργασίες παλινδρόµησης για να κατασκευάσει ένα µοντέλο παλινδρόµησης. Τα µοντέλα παλινδρόµησης περιλαµβάνουν τις ακόλουθες µεταβλητές[1]:
- Οι άγνωστες παράµετροι συσχέτισης που δηλώνονται ως (διάνυσµα).
- Οι ανεξάρτητες µεταβλητές (διάνυσµα).
- Η εξαρτώµενη µεταβλητή .
Ένα µοντέλο παλινδρόµησης συσχετίζει το Υ σε µία συνάρτηση παλιδρόμησης/regression των και . . Ο συνήθης φορµαλισµός είναι .
Η Ανάλυση Παλινδρόµησης μας βοηθά να κατανοήσουμε την μεταβολή της εξαρτώµενης µεταβλητής Υ όταν µεταβάλλεται µία από τις ανεξάρτητες µεταβλητές Χ, ενώ οι άλλες ανεξάρτητες µεταβλητές κρατιούνται σταθερές. Συνήθως, επιδιώκεται να εξακριβωθεί η αιτιώδης επίδραση µιας µεταβλητής επάνω σε άλλη. Για παράδειγμα, η επίδραση της αύξησης τιµών προϊόντων µε την προσφορά/ζήτηση. Η επίδραση της παροχής χρημάτων στο ρυθμό πληθωρισμού. Για τέτοια ζητήματα, συγκεντρώνονται τα δεδομένα που αφορούν τις µεταβλητές ενδιαφέροντος και υιοθετείται η παλινδρόµηση για να υπολογίσει την ποσοτική επίδραση των µεταβλητών επάνω στη µεταβλητή που επηρεάζουν. Αξιολογείται επίσης η "στατιστική σημασία" των κατ' εκτίμηση συσχετίσεων, δηλαδή ο βαθµός εµπιστοσύνης (confidence) ότι η αληθινή συσχέτιση είναι κοντά στην κατ' εκτίμηση. Η ανάλυση παλινδρόµησης για πρόβλεψη και πρόγνωση έχει ουσιαστική επικάλυψη µε τον τοµέα της µηχανικής µάθησης [1].
Γραμμική παλινδρόμηση[Επεξεργασία | επεξεργασία κώδικα]
Η παλινδρόμηση είναι μια τεχνική που χρησιμοποιείται για τη μοντελοποίηση και την ανάλυση αριθμητικών δεδομένων, μιας εξαρτημένης μεταβλητής και κάποιων ανεξάρτητων μεταβλητών. Το μοντέλο είναι μια συνάρτηση συσχέτισης της εξαρτημένης μεταβλητής από τις ανεξάρτητες. Η μοντελοποίηση μπορεί να γίνει χωρίς να είναι γνωστή απο πριν η γνώση για τον τρόπο με τον οποίο συνδέεται η εξαρτημένη μεταβλητή από τις ανεξάρτητες και τότε ονομάζεται εμπειρική μοντελοποίηση.Στην γραμμική παλινδρόμηση, η απαίτηση του μοντέλου που θα παραχθεί είναι: η εξαρτημένη μεταβλητή yi να είναι ένας γραμμικός συνδυασμός των ανεξαρτήτων μεταβλητών[6].
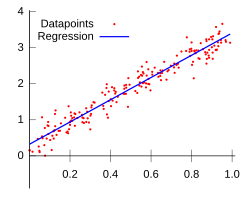
Απλή Γραμμική παλινδρόμηση[Επεξεργασία | επεξεργασία κώδικα]
Στην απλή γραμμική παλινδρόμηση υπάρχει η ανεξάρτητη μεταβλητή , και δύο παράμετροι . Το μοντέλο έχει τη μορφή[6]:
- με όπου είναι το σφάλμα της πρόβλεψης.
Παραδοχές για την εφαρμογή του απλού γραμμικού μοντέλου[Επεξεργασία | επεξεργασία κώδικα]
Γραμμικότητα[Επεξεργασία | επεξεργασία κώδικα]
Η κατανομή της έχει, για τα διάφορα επίπεδα της , μέση τιμή ή όπου, και παράμετροι που εκτιμώνται από το δείγμα . Άρα, υποθέτουμε ότι οι μέσες τιμές της , για τα διάφορα επίπεδα της Χ, είναι γραμμικές συναρτήσεις της Χ (ότι βρίσκονται δηλαδή σε ευθεία γραμμή). Σημειώνουμε ότι στο μοντέλο , τυχαίες μεταβλητές είναι μόνο οι και [7].
Ομοσκεδαστικότητα-Σταθερότητα Διασποράς[Επεξεργασία | επεξεργασία κώδικα]
Οι κατανομές της έχουν ίδια διασπορά για όλα τα επίπεδα της , δηλαδή, . [7].
Ανεξαρτησία[Επεξεργασία | επεξεργασία κώδικα]
Οι τιμές της Υ που αντιστοιχούν στα διάφορα επίπεδα της Χ είναι ανεξάρτητες μεταξύ τους. Εξαρτημένα Υ εμφανίζονται συνήθως όταν παίρνουμε παρατηρήσεις από την ίδια πειραματική μονάδα σε διαφορετικές χρονικές στιγμές (π.χ. μετράμε την πίεση ή το βάρος του ιδίου ατόμου ανά εβδομάδα). Επίσης, σε περιπτώσεις όπου χρησιμοποιούνται μηχανές (π.χ. όργανα μέτρησης, κ.τλ) που αλλάζει η απόδοσή ανάλογα με τη χρήση αν ο χειριστής βελτιώνεται (ή χειροτερεύει) με την πάροδο του χρόνου. Είναι επομένως αναγκαίο, όταν έχουμε πειραματικά δεδομένα που παίρνονται με χρονική σειρά, να κάνουμε ένα διάγραμμα υπολοίπων ως προς το χρόνο έστω και αν ο χρόνος δεν χρησιμοποιείται ως μεταβλητή στο μοντέλο [7].
Κανονικότητα[Επεξεργασία | επεξεργασία κώδικα]
Η κατανομή της για όλα τα επίπεδα της είναι κανονική. Η κανονικότητα μπορεί να ελεγχθεί με διάφορους τρόπους όπως:
- Με ιστόγραμμα
- Με φυλλογράφημα (steam and leaf plot)
- Με θηκόγραμμα (box plot)
- Με διάγραμμα πιθανοτήτων (normal probability plot)
- Με στατιστικούς ελέγχους καλής προσαρμογής (goodness–of-fit test) όπως KolmogorovSmirnov test ή test.
Όταν διαπιστώνεται παραβίαση της κανονικότητας μπορούμε, σε πολλές περιπτώσεις, να αντιμετωπίσουμε το πρόβλημα με κατάλληλους μετασχηματισμούς στις μεταβλητές[7].
Λογιστική Παλινδρόµηση[Επεξεργασία | επεξεργασία κώδικα]
Το λογιστικό μοντέλο είναι ένα μη γραμμικό μοντέλο, τα σφάλματα, του οποίου δεν υπακούν στην κανονική κατανομή και η μεταβλητή απόκρισης είναι διακριτή.
Η λογιστική παλινδρόμηση χρησιμοποιείται όταν επιθυμούμε να προβλέψουμε την απουσία ή την παρουσία ενός χαρακτηριστικού, ή ενός συμβάντος. Είναι μια γενίκευση της απλής γραμμικής παλινδρόμησης για την

περίπτωση όπου η εξαρτημένη μεταβλητή (Υ) είναι δίτιμη ( δηλαδή παίρνει την τιμή 0 όταν απουσιάζει το χαρακτηριστικό ή την τιμή 1 όταν υπάρχει το χαρακτηριστικό)[8]. Ένα παράδειγμα της εφαρμογής της είναι η εξέταση της εμφάνισης στεφανιαίας νόσου σε ένα νοσοκομείο σε ένα δείγμα ανδρών σε σχέση με την ηλικία, εάν καπνίζουν, τη συστολική και διαστολική πίεση του αίματος, τα επίπεδα της χοληστερόλης και το βάρος τους. Σε αυτή την περίπτωση, κωδικοποίησαν με 0 τα άτομα που δεν έχουν πάθει έμφραγμα τα τελευταία 10 χρόνια και με 1 τα άτομα που έχουν υποστεί έμφραγμα.
Το γραμμικό μοντέλο είναι αδύνατο να χρησιμοποιηθεί όταν η μεταβλητή Υ είναι δυαδική και έχουμε τα εξής τρία προβλήματα:
- Τα σφάλματα δεν είναι κανονικά.
- Τα σφάλματα έχουν άνισες διασπορές
- Περιορισμός στη συνάρτηση απόκρισης
Παρόλο που στα δύο πρώτα προβλήματα είναι δυνατό να τα παραλείψουμε και να χρησιμοποιήσουμε την γραμμική παλινδρόµηση, εφαρμόζοντας κάποιες άλλες τεχνικές, το τρίτο πρόβλημα μας το απαγορεύει ρητά, γιατί δεν μπορεί να αντιμετωπιστεί με διαφορετικό τρόπο.
Απλό Λογιστικό Μοντέλο[Επεξεργασία | επεξεργασία κώδικα]
Το μοντέλο που χρησιμοποιούμε όταν η Yi είναι δίτιμη είναι το λογιστικό, το οποίο ορίζεται ως εξής: όπου : ανεξάρτητη τ.μ. Bernoulli και
όπου [8]
Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]
- Xiangliang Zhang. «Linear Regression» (PDF). King Abdullah University of Science and Technology. Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 10 Νοεμβρίου 2014. Ανακτήθηκε στις 30 Απριλίου 2013. (pdf)
Αναφορές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ 1,0 1,1 1,2 ΓΙΑΝΝΗΣ ΚΟΚΚΙΝΟΣ.,(2011). ΠΑΡΑΛΛΗΛΟΙ ΑΛΓΟΡΙΘΜΟΙ ΕΞΟΡΥΞΗΣ ΓΝΩΣΗΣ ΑΠΟ ΒΑΣΕΙΣ ΔΕΔΟΜΕΝΩΝ ΜΕ ΤΕΧΝΗΤΑ ΝΕΥΡΩΝΙΚΑ ΔΙΚΤΥΑ ΚΑΙ ΜΗΧΑΝΕΣ ΔΙΑΝΥΣΜΑΤΩΝ ΥΠΟΣΤΗΡΙΞΗΣ.Ανακτήθηκε στις 2 Οκτώβρη από http://dspace.lib.uom.gr/bitstream/2159/14399/1/KokkinosIoannisMsc2011.pdf
- ↑ Μιχάλης Βαζιργιάννης, Μαρία Χαλκίδη, Εξόρυξη Γνώσης από Βάσεις Δεδομένων και τον Παγκόσμιο Ιστό, Εκδ. Gutenberg
- ↑ ΝΤΑΛΛΑ ΜΙΡΕΛΑ.,(2009). ΕΦΑΡΜΟΓΗ ΑΛΓΟΡΙΘΜΩΝ ΕΠΑΓΩΓΙΚΟΥ ΛΟΓΙΚΟΥ ΠΡΟΓΡΑΜΜΑΤΙΣΜΟΥ ΣΤΗ ΣΧΕΣΙΑΚΗ ΕΞΟΡΥΞΗ ∆Ε∆ΟΜΕΝΩΝ.Ανακτήθηκε στις 2 Οκτώβρη από http://nemertes.lis.upatras.gr/jspui/bitstream/10889/2656/1/Nimertis_Dalla.pdf
- ↑ Κεχαγιά – Παρδάλη Ευθαλία.,(2006). Αλγόριθμοι Εξόρυξης Χωρικών ∆εδομένων Εφαρμογή σε Αλγόριθμους Συσταδοποίησης.Ανακτήθηκε στις 2 Οκτώβρη από http://www.dbnet.ece.ntua.gr/~kpatro/theses/geodb/Kehagia_thesis.pdf Αρχειοθετήθηκε 2015-05-12 στο Wayback Machine.
- ↑ 5,0 5,1 Ηλίας Αθανασιάδης.,(2005). Μια κοινωνιολογική και ιστορική παρουσίαση της Στατιστικής.Ανακτήθηκε στις 6 Οκτώβρη από http://www.rhodes.aegean.gr/ptde/revmata/issue3/1ΒΙΒΛΙΟΠΑΡΟΥΣΙΑΣΗ%20ΑΘΑΝΑΣΙΑΔΗΣ%20ΡΕΥ%203.pdf
- ↑ 6,0 6,1 Τσαρακτσίδης Γεώργιος.,(2008). Εξόρυξη γνώσης από βάση δεδομένων ηλεκτρονικών δημοπρασιών από τον δικτυακό τόπο eBay.Ανακτήθηκε στις 6 Οκτώβρη από http://vivliothmmy.ee.auth.gr/76/1/ΔΙΠΛΩΜΑΤΙΚΗ_ΕΡΓΑΣΙΑ_-_ΤΣΑΡΑΚΤΣΙΔΗΣ_ΓΕΩΡΓΙΟΣ_(4006).pdf
- ↑ 7,0 7,1 7,2 7,3 Παπαδόπουλος Γεώργιος. Εργαστήριο. Μαθηματικών & Στατιστικής. Ανακτήθηκε στις 8 Οκτώβρη από http://www.aua.gr/gpapadopoulos/files/regression9.pdf
- ↑ 8,0 8,1 Ξενή Μαρία. Λογιστική Παλινδρόμηση & Διαχωριστική Ανάλυση. Ανακτήθηκε στις 8 Οκτώβρη από http://nemertes.lis.upatras.gr/jspui/bitstream/10889/5174/1/Diplwmatiki.pdf























