Πόσο είναι το μήκος των ακτών της Βρετανίας; Στατιστική αυτοομοιότητα και μορφοκλασματική διάσταση
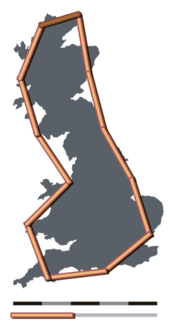

Πόσο είναι το μήκος των ακτών τις Βρετανίας; Στατιστική αυτοομοιότητα και μορφοκλασματική διάσταση (How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension) είναι ο τίτλος μίας διατριβής του μαθηματικού Μπενουά Μάντελμπροτ, η οποία πρωτοδημοσιεύτηκε στο περιοδικό Science το 1967.[1] Σε αυτή τη διατριβή ο Μάντελμπροτ εξετάζει αυτοόμοιες καμπύλες με διάσταση Χάουσντορφ μεταξύ 1 και 2. Αυτές οι καμπύλες είναι παραδείγματα φράκταλ, αν και ο Μάντελμπροτ δεν χρησιμοποιεί τον όρο στη διατριβή, καθώς τον εισηγήθηκε το 1975. Η διατριβή αποτελεί την πρώτη του Μάντελμπροτ πάνω στο θέμα των φράκταλ.[2]
Περίληψη[Επεξεργασία | επεξεργασία κώδικα]
Η διατριβή εξετάζει το παράδοξο των ακτογραμμών: την ιδιότητα του μετρούμενου μήκους της ακτογραμμής να εξαρτάται από την κλίμακα μέτρησης. Εμπειρικά δεδομένα υποδεικνύουν ότι όσο μικρότερο είναι το βασικό μήκος μέτρησης, τόσο μεγαλύτερο προκύπτει το μετρούμενο μήκος. Αν κανείς μετρούσε την ακτογραμμή με ένα χάρακα ενός μέτρου θα έβγαζε μικρότερο αποτέλεσμα από μία μέτρηση με ένα χάρακα 30 εκατοστών. Αυτό προκύπτει γιατί στη δεύτερη περίπτωση ο χάρακας θα τοποθετούνταν σε πιο καμπύλη πορεία από αυτή της πρώτης περίπτωσης. Τα εμπειρικά στοιχεία υποδεικνύουν ένα κανόνα ο οποίος αν γενικευθεί δείχνει ότι το μετρούμενο μήκος αυξάνεται χωρίς όριο καθώς η κλίμακα μέτρησης μειώνεται προς το μηδέν.
Από την εξέταση συνεπάγεται ότι δεν έχει νόημα η συζήτηση για το μήκος μιας ακτογραμμής, και πρέπει να βρεθεί ένας άλλος τρόπος ποσοτικοποίησης της. Ο Μάντελμπροτ εξετάζει ένα εμπειρικό νόμο που ανακαλύφθηκε από τον Λιούις Φράι Ρίτσαρντσον, ο οποίος παρατήρησε ότι το μετρούμενο μήκος L(G) διαφόρων γεωγραφικών ορίων ήταν συνάρηση της κλίμακας μέτρησης G. Συγκεντρώνοντας δεδομένα από διάφορα παραδείγματα ο Ρίτσαρντσον συμπέρανε ότι το L(G) μπορεί να προσεγγιστεί από μία συνάρτηση της μορφής
όπου το M είναι θετική σταθερά και το D είναι σταθερά, καλούμενη διάσταση, και είναι μεγαλύτερη ή ίση του 1. Διαισθητικά, αν η ακτογραμμή φαίνεται λεία θα πρέπει να έχει διάσταση κοντά στο 1, και όσο πιο ανώμαλη είναι τόσο πιο κοντά στο 2 θα πρέπει να είναι η διάστασή της. Τα παραδείγματα στην έρευνα του Ρίτσαρντσον έχουν διαστάσεις που κυμαίνονται από το 1.02 για την ακτογραμμή της Νότιας Αφρικής έως 1.25 για την δυτική ακτογραμμή της Βρετανίας.
Ο Μάντελμπροτ στη συνέχεια περιγράφει διάφορες μαθηματικές καμπύλες, που σχετίζονται με την νιφάδα του Κοχ, και οι οποίες ορίζονται με τέτοιο τρόπο που είναι αυστηρώς αυτοόμοιες. Ο Μάντελμπροτ δείνει το πως υπολογίζεται η διάσταση Χάουσντορφ για κάθε μία από αυτές, η οποία έχει διάσταση D μεταξύ 1 και 2 (αναφέρει επίσης, αλλά δεν δίνει κατασκευή, την καμπύλη Πεάνο, η οποία έχει διάσταση ακριβώς 2). Σημειώνει ότι η προσέγγιση αυτών των καμπυλών με τμήματα μήκους G έχουν μήκος της μορφής . Η ομοιότητα με τον νόμο του Ρίτσαρντσον είναι αξιοσημείωτη. Στη διατριβή δεν ισχυρίζεται ότι κάποια ακτογραμμή έχει στην πραγματικότητα μορφοκλασματική διάσταση. Αντιθέτως, σημειώνει ότι ο εμπειρικός νόμος του Ρίτσαρντσον είναι συμβατός με την ιδέα ότι γεωγραφικές καμπύλες, όπως οι ακτογραμμές, μπορούν να μοντελοποιηθούν με τυχαία αυτοόμοια σχήματα με μορφοκλασματική διάσταση.
Προς το τέλος ο Μάντελμπροτ εξετάζει εν συντομία το πως μπορεί κανείς να προσεγγίσει την μελέτη φρακταλοειδών αντικειμένων της φύσης τα οποία φαίνονται περισσότερο τυχαία παρά κανονικά. Για αυτό ορίζει στατιστικά αυτοόμοια σχήματα και λέει ότι αυτά συναντώνται στη φύση.
Η διατριβή αυτή είναι σημαντική καθώς αποτελεί το σημείο καμπής στην πρώιμη σκέψη του Μάντελμπροτ για τα φράκταλ.[3] Είναι παράδειγμα σύνδεσης μαθηματικών αντικειμένων με φυσικές μορφές το οποίο είναι θέμα του μεγαλύτερου μέρους του μεταγενέστερου έργου του.
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Benoît Mandelbrot, 1967, How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension. Science, New Series, Vol. 156, No. 3775. (May 5, 1967), σσ. 636-638. doi:10.1126/science.156.3775.636
- ↑ "Dr. Mandelbrot traced his work on fractals to a question he first encountered as a young researcher: how long is the coast of Britain?", Benoît Mandelbrot, Novel Mathematician, Dies at 85, The New York Times
- ↑ "What is the essence of a coastline, for example ? Mandelbrot asked this question in a paper that became a turning point for his thinking: "How Long Is the Coast of Britain"", James Gleick, Chaos: Making a New Science, σ.94.


