Κώνος φωτός
| Αυτό το λήμμα δεν ανήκει σε καμία κατηγορία. Μπορείτε να βοηθήσετε προσθέτοντας μία ή περισσότερες κατηγορίες σε αυτό. Αφαιρέστε αυτό το πρότυπο μόλις προσθέσετε κατηγορίες στη σελίδα. |

Στην ειδική και γενική σχετικότητα, ένας κώνος φωτός είναι το μονοπάτι που θα διανύσει μια λάμψη φωτός, που προέρχεται από ένα μόνο γεγονός στο χωροχρόνο (εντοπισμένο σε ένα μόνο σημείο στο διάστημα και μια στιγμή στο χρόνο) και ταξιδεύει προς όλες τις κατευθύνσεις.
Λεπτομέριες[Επεξεργασία | επεξεργασία κώδικα]
Αν κάποιος φανταστεί το φως που περιορίζεται σε ένα δισδιάστατο επίπεδο, το φως από το φλας απλώνεται σε έναν κύκλο μετά το συμβάν E και εάν γράψουμε τον αναπτυσσόμενο κύκλο με τον κατακόρυφο άξονα του γραφήματος να αντιπροσωπεύει το χρόνο, το αποτέλεσμα είναι ένας κώνος, γνωστός ως μελλοντικός κώνος φωτός. Ο κώνος του παρελθόντος φωτός συμπεριφέρεται όπως ο μελλοντικός κώνος φωτός αντίστροφα, ένας κύκλος που συστέλλεται σε ακτίνα με την ταχύτητα του φωτός έως ότου συγκλίνει σε ένα σημείο στην ακριβή θέση και χρόνο του συμβάντος Ε. Στην πραγματικότητα, υπάρχουν τρεις διαστάσεις χώρου, έτσι το φως θα σχημάτιζε πραγματικά μια διαστελλόμενη ή συσπειρωμένη σφαίρα σε τρισδιάστατο χώρο και όχι έναν κύκλο σε 2D, και ο κώνος φωτός θα ήταν στην πραγματικότητα μια τετραδιάστατη έκδοση ενός κώνου του οποίου οι διατομές σχηματίζουν τρισδιάστατες σφαίρες (ανάλογο σε έναν κανονικό τρισδιάστατο κώνο του οποίου οι διατομές σχηματίζουν 2D κύκλους), αλλά η ιδέα είναι πιο εύκολο να απεικονιστεί με τον αριθμό των χωρικών διαστάσεων να μειώνεται από τρεις σε δύο.
Αυτή η άποψη της ειδικής σχετικότητας προτάθηκε για πρώτη φορά από τον πρώην καθηγητή του Albert Einstein Χέρμαν Μινκόβσκι και είναι γνωστή ως χώρος Minkowskii. Ο σκοπός ήταν να δημιουργηθεί ένας αμετάβλητος χωροχρόνος για όλους τους παρατηρητές. Για να υποστηρίξει την αιτιώδη συνάφεια, ο Μινκόβσκι περιόρισε τον χωροχρόνο σε μη ευκλείδεια υπερβολική γεωμετρία.[1]
Επειδή τα σήματα και άλλες αιτιώδεις επιρροές δεν μπορούν να ταξιδέψουν γρηγορότερα από το φως (βλ. Ειδική σχετικότητα), ο κώνος φωτός παίζει ουσιαστικό ρόλο στον καθορισμό της έννοιας της αιτιότητας: για ένα δεδομένο συμβάν Ε, το σύνολο των γεγονότων που βρίσκονται πάνω ή μέσα στον κώνο του παρελθόντος του Ε θα ήταν επίσης το σύνολο όλων των γεγονότων που θα μπορούσαν να στείλουν ένα σήμα που θα είχε χρόνο να φτάσει στο Ε και να το επηρεάσει με κάποιο τρόπο. Για παράδειγμα, δέκα χρόνια πριν από το E, αν λάβουμε υπόψη το σύνολο όλων των γεγονότων στον προηγούμενο φωτεινό κώνο του E που συνέβη εκείνη την εποχή, το αποτέλεσμα θα ήταν μια σφαίρα (2D: δίσκος) με ακτίνα δέκα έτη φωτός με επίκεντρο τη θέση όπου θα εμφανιστεί το Ε. Έτσι, οποιοδήποτε σημείο πάνω ή μέσα στη σφαίρα θα μπορούσε να στείλει ένα σήμα που κινείται με την ταχύτητα του φωτός ή πιο αργά που θα είχε χρόνο να επηρεάσει το συμβάν Ε, ενώ σημεία έξω από τη σφαίρα εκείνη τη στιγμή δεν θα μπορούσαν να έχουν καμία αιτιώδη επίδραση στο Ε Ομοίως, το σύνολο των γεγονότων που βρίσκονται πάνω ή μέσα στον μελλοντικό φωτεινό κώνο του Ε θα είναι επίσης το σύνολο των γεγονότων που θα μπορούσαν να λάβουν ένα σήμα που αποστέλλεται από τη θέση και τον χρόνο του Ε, οπότε ο μελλοντικός κώνος φωτός περιέχει όλα τα γεγονότα που θα μπορούσε δυνητικά να επηρεαστεί αιτιωδώς από την Ε. Τα γεγονότα που δεν βρίσκονται ούτε στο παρελθόν, ούτε στο μέλλον του κώνου φωτός του Ε δεν μπορούν να επηρεάσουν ή να επηρεαστούν από το Ε στη σχετικότητα και ονομάζονται οπουδήποτε αλλού.[2]
Μαθηματική κατασκευή[Επεξεργασία | επεξεργασία κώδικα]
Στην ειδική σχετικότητα, ένας κώνος φωτός (ή μηδενικός κώνος) είναι η επιφάνεια που περιγράφει τη χρονική εξέλιξη μιας λάμψης φωτός στον χωροχρόνο του Μινκόβσκι. Αυτό μπορεί να απεικονιστεί σε 3 διαστάσεις χώρου εάν οι δύο οριζόντιοι άξονες επιλεγούν ως χωρικές διαστάσεις, ενώ ο κάθετος άξονας είναι ο χρόνος.[3]
Ο κώνος φωτός κατασκευάζεται ως εξής: Λαμβάνοντας ως συμβάν έστω p την λάμψη φωτός (παλμός φωτός) τη στιγμή t0, όλα τα γεγονότα που μπορούν να επιτευχθούν με αυτόν τον παλμό από το p σχηματίζουν τον μελλοντικό κώνο φωτός του p, ενώ εκείνα τα γεγονότα που μπορούν να στείλουν έναν παλμό φωτός σε p σχηματίζουν τον προηγούμενο κώνο φωτός του.
Δεδομένου ενός συμβάντος Ε ο κώνος φωτός ταξινομεί όλα τα γεγονότα στο χωροχρόνο σε 5 διαφορετικές κατηγορίες:
- Εκδηλώσεις για τον μελλοντικό κώνο φωτός του E.
- Γεγονότα σχετικά με τον προηγούμενο κώνο φωτός του Ε.
- Τα γεγονότα εντός του μελλοντικού κώνου φωτός του Ε είναι εκείνα που επηρεάζονται από ένα σωματιδιακό υλικό που εκπέμπεται στο Ε.
- Τα γεγονότα μέσα στον προηγούμενο κώνο φωτός του Ε είναι εκείνα που μπορούν να εκπέμψουν ένα σωματικό σωματίδιο και να επηρεάσουν αυτό που συμβαίνει στο Ε.
- Όλα τα άλλα γεγονότα βρίσκονται στο (απόλυτο) οτιδήποτε αλλού του E και είναι αυτά που δεν μπορούν να επηρεάσουν ή να επηρεαστούν από το E.
Οι παραπάνω ταξινομήσεις ισχύουν σε οποιοδήποτε πλαίσιο αναφοράς. δηλαδή, ένα γεγονός που κρίνεται ότι βρίσκεται στον κώνο φωτός από έναν παρατηρητή, θα κριθεί επίσης ότι είναι στον ίδιο κώνο φωτός από όλους τους άλλους παρατηρητές, ανεξάρτητα από το πλαίσιο αναφοράς τους. Αυτός είναι ο λόγος για τον οποίο η ιδέα είναι τόσο ισχυρή.
Τα παραπάνω αναφέρονται σε ένα συμβάν που συμβαίνει σε μια συγκεκριμένη τοποθεσία και σε μια συγκεκριμένη ώρα. Το να πούμε ότι ένα συμβάν δεν μπορεί να επηρεάσει ένα άλλο σημαίνει ότι το φως δεν μπορεί να περάσει από τη θέση του ενός στο άλλο σε δεδομένο χρονικό διάστημα. Το φως από κάθε συμβάν θα φτάσει τελικά στην προηγούμενη τοποθεσία του άλλου, αλλά αφού συμβούν αυτά τα γεγονότα.
Καθώς ο χρόνος προχωρά, ο μελλοντικός φωτός κώνος ενός δεδομένου γεγονότος θα μεγαλώσει και θα περιλαμβάνει όλο και περισσότερες τοποθεσίες (με άλλα λόγια, η τρισδιάστατη σφαίρα που αντιπροσωπεύει την εγκάρσια τομή του 4D φωτός κώνου σε μια συγκεκριμένη χρονική στιγμή γίνεται μεγαλύτερη με την πάροδο του χρόνου). Ωστόσο, αν φανταστούμε ότι ο χρόνος τρέχει αντίστροφα από ένα δεδομένο γεγονός, ο κώνος του παρελθόντος φωτός του γεγονότος θα περιλάμβανε επίσης όλο και περισσότερες τοποθεσίες σε παλαιότερες και παλαιότερες εποχές. Οι πιο μακρινές τοποθεσίες θα είναι σε μεταγενέστερες εποχές: για παράδειγμα, αν λάβουμε υπόψη τον παρελθόντα κώνο φωτός ενός γεγονότος που λαμβάνει χώρα στη Γη σήμερα, ένα αστέρι 10.000 έτη φωτός μακριά θα ήταν μόνο μέσα στον κώνο του παρελθόντος φωτός σε χρονικά διαστήματα 10.000 ετών ή περισσότερο στο παρελθόν. Ο προηγούμενος κώνος φωτός ενός γεγονότος στη σημερινή Γη, στις άκρες του, περιλαμβάνει πολύ μακρινά αντικείμενα (κάθε αντικείμενο στο παρατηρήσιμο σύμπαν), αλλά μόνο όπως φαίνονταν πολύ καιρό πριν, όταν το Σύμπαν ήταν νέο.
Δύο γεγονότα σε διαφορετικές τοποθεσίες, ταυτόχρονα (σύμφωνα με ένα συγκεκριμένο πλαίσιο αναφοράς), βρίσκονται πάντα έξω από τους παλιούς και μελλοντικούς κώνους φωτός του άλλου , το φως δεν μπορεί να ταξιδέψει ακαριαία (αυτό προκύπτει στο δικό μας αδρανειακό σύστημα,οι εξισώσεις της ειδ.σχετικότητας για το φως δίνουν μηδέν χρόνο μεταξύ δύο γεγονότων Α και Β, το ίδιο ισχύει για το χωροχρονικό μήκος). Άλλοι παρατηρητές μπορεί να δουν τα γεγονότα να συμβαίνουν σε διαφορετικές χρονικές στιγμές και σε διαφορετικές τοποθεσίες, αλλά με τον ένα ή τον άλλο τρόπο, τα δύο γεγονότα θα φαίνονται ομοίως έξω από τους κώνους του άλλου.
Εάν χρησιμοποιείται σύστημα μονάδων όπου η ταχύτητα του φωτός στο κενό ορίζεται ως ακριβώς 1, για παράδειγμα εάν ο χώρος μετριέται σε δευτερόλεπτα φωτός και ο χρόνος μετράται σε δευτερόλεπτα, τότε, εφόσον ο άξονας του χρόνου έλκεται ορθογώνια στους χωρικούς άξονες, καθώς ο κώνος διχοτομεί τους άξονες του χρόνου και του χώρου, θα δείχνει κλίση 45 °, επειδή το φως διανύει απόσταση ενός φωτός-δευτερολέπτου στο κενό κατά τη διάρκεια ενός δευτερολέπτου. Δεδομένου ότι η ειδική σχετικότητα απαιτεί η ταχύτητα του φωτός να είναι ίση σε κάθε αδρανειακό πλαίσιο, όλοι οι παρατηρητές πρέπει να φτάσουν στην ίδια γωνία 45 ° για τους κώνους φωτός τους ή διότι η εφ(45 °) ισούται με 1. Συνήθως ένα διάγραμμα Minkowski χρησιμοποιείται για να απεικονίσει αυτήν την ιδιότητα των μετασχηματισμών του Lorentz. Αλλού, αναπόσπαστο μέρος των φωτεινών κώνων είναι η περιοχή του χωροχρόνου έξω από τον κώνο φωτός σε ένα δεδομένο γεγονός (ένα σημείο στο χωροχρόνο). Τα γεγονότα που βρίσκονται αλλού το ένα από το άλλο είναι αμοιβαία μη παρατηρήσιμα και δεν μπορούν να συνδεθούν αιτιακά.
(Το σχήμα των 45 ° έχει νόημα μόνο στον χώρο-χώρο, καθώς προσπαθούμε να κατανοήσουμε το χωροχρόνο κάνοντας σχέδια χώρου-χώρου. Η κλίση του χώρου-χώρου μετριέται με γωνίες και υπολογίζεται με τριγωνομετρικές συναρτήσεις. Μετράται η κλίση του χωροχρόνου με ταχύτητα και υπολογίζεται με υπερβολικές συναρτήσεις.)
Γενική Σχετικότητα[Επεξεργασία | επεξεργασία κώδικα]
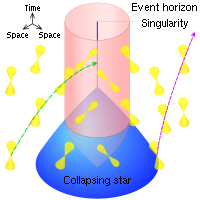
Σε επίπεδο χωροχρόνο, ο μελλοντικός φωτός κώνος ενός γεγονότος είναι το όριο του αιτιώδους μέλλοντός του και ο κώνος του παρελθόντος είναι το όριο του αιτιώδους παρελθόντος του.
Σε έναν καμπύλο χωροχρόνο, αν υποθέσουμε ότι ο χωροχρόνος είναι παγκοσμίως υπερβολικός, εξακολουθεί να ισχύει ότι ο μελλοντικός κώνος φωτός ενός γεγονότος περιλαμβάνει το όριο του αιτιώδους μέλλοντός του (και ομοίως για το παρελθόν). Ωστόσο, οι βαρυτικοί φακοί μπορούν να προκαλέσουν αναδίπλωση μέρους του κώνου φωτός στον εαυτό του, με τέτοιο τρόπο ώστε μέρος του κώνου να βρίσκεται αυστηρά μέσα στο αιτιώδες μέλλον (ή παρελθόν) και όχι στο όριο.
Οι φωτεινοί κώνοι επίσης δεν μπορούν να γέρνουν έτσι ώστε να είναι «παράλληλοι» αυτό αντανακλά το γεγονός ότι ο χωροχρόνος είναι καμπύλος και είναι ουσιαστικά διαφορετικός από τον χώρο του Μινκόβσκι. Σε περιοχές κενού (εκείνα τα σημεία του χωροχρόνου χωρίς ύλη), αυτή η αδυναμία κλίσης όλων των κώνων φωτός έτσι ώστε να είναι όλοι παράλληλοι αντανακλάται στη μη εξαφάνιση του τανυστή Weyl.
Δείτε επίσης[Επεξεργασία | επεξεργασία κώδικα]
Αναφορές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Cox, Brian, 1968- (2009). Why does E=mc2 : (and why should we care?). Forshaw, J. R. (Jeffrey Robert), 1968-. Cambridge, MA: Da Capo Press. ISBN 978-0-306-81758-8. OCLC 246894061.
- ↑ Curiel, Erik (2019). «Singularities and Black Holes > Light Cones and Causal Structure (Stanford Encyclopedia of Philosophy)». plato.stanford.edu. Stanford Encyclopedia of Philosophy. Ανακτήθηκε στις 3 Μαρτίου 2020.
- ↑ Penrose, Roger (2005), The Road to Reality, London: Vintage Books, ISBN 978-0-09-944068-0
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- The Einstein-Minkowski Spacetime: Introducing the Light Cone
- The Paradox of Special Relativity
- RSS feed of stars in one's personal light cone
