Ιδιοτιμές και ιδιοδιανύσματα

Σ'αυτή τη διάτμητη χαρτογράφηση το κόκκινο βέλος αλλάζει κατεύθυνση, αλλά το μπλε όχι. Το μπλε βέλος είναι ένα ιδιοδιάνυσμα αυτής της διάτμητης χαρτογράφησης, και αφού το μήκος του είναι αμετάβλητο, η ιδιοτιμή του είναι ίση με 1.

Ενα ιδιοδιάνυσμα ενός τετραγωνικού πίνακα $A$ είναι ένα μη μηδενικό διάνυσμα $v$ που, όταν πολλαπλασιαστεί με τον $A$, ισούται με το αρχικό διάνυσμα, πολλαπλασιασμένο με έναν αριθμό $\lambda$, έτσι ώστε:

$Av=\lambda v$

Ο αριθμός $\lambda$ ονομάζεται ιδιοτιμή του $A$ που αντιστοιχεί στο $v$.

Στην αναλυτική γεωμετρία, για παράδειγμα, ένα διάνυσμα με 3 στοιχεία, μπορεί να ταυτιστεί με ένα βέλος σε ένα τρισδιάστατο χώρο, ξεκινώντας από την αρχή των αξόνων. Σ'αυτην την περιπτωση, ένα ιδιοδιάνυσμα ενός 3x3 πίνακα $A$ είναι ένα βέλος η κατεύθυνση του οποίου ή διατηρείται, ή γίνεται ακριβώς η αντίθετη, μετά τον πολλαπλασιασμό με τον $A$. Η αντίστοιχη ιδιοτιμή είναι αυτή που καθορίζει πως αλλάζει το μήκος του βέλους από τη διαδικασία, και εάν η κατεύθυνση του αντιστρέφεται ή όχι.

Στην αφηρημένη γραμμική άλγεβρα, οι έννοιες αυτές συνήθως επεκτείνονται σε πιο γενικές καταστάσεις, όπου οι παράγοντες που χρησιμοποιούνται σε πραγματική κλίμακα, αντικαθίστανται από σώματα κάθε διάστασης (όπως για παράδειγμα οι αλγεβρικοί ή οι μιγαδικοί αριθμοί), οι καρτεσιανές συντεταγμένες $\mathbb {R} ^{n}$ που αντικαθίστανται από τυχαίους διανυσματικούς χώρους (όπως για παράδειγμα των συνεχών συναρτήσεων, των πολυωνύμων ή των τριγωνομετρικών σειρών), και ο πολλαπλασιασμός πινάκων που αντικαθίσταται από κάθε γραμμικό τελεστή που απεικονίζει διανύσματα σε διανύσματα (όπως η παράγωγος από το διαφορικό λογισμό). Σ'αυτές τις περιπτώσεις, το "διάνυσμα" σε "ιδιοδιάνυσμα" μπορεί να αντικατασταθεί από έναν πιο ακριβή όρο, όπως "ιδιοσυνάρτηση","ιδιομορφή","ιδιοπροσωπία", ή "ιδιοκατάσταση". Επομένως, για παράδειγμα, η εκθετική συνάρτηση $f(x)=a^{x}$ είναι μια ιδιοσυνάρτηση του παράγωγου φορέα " ${}'$ ", με ιδιοτιμή $\lambda =\ln a$, αφού η παράγωγος της είναι η $f'(x)=(\ln a)a^{x}=\lambda f(x)$.

Το σύνολο όλων των ιδιοδιανυσμάτων ενός πίνακα (ή γραμμικού τελεστή), με το καθένα να ταιριάζει στην αντίστοιχη ιδιοτιμή του, καλείται το "ιδιοσύστημα" του πίνακα αυτού. Ο ιδιοχώρος ενός πίνακα $A$ είναι το σύνολο όλων των ιδιοδιανυσμάτων με την ίδια ιδιοτιμή, συμπεριλαμβανομένου και του μηδενικού διανύσματος. Μια ιδιοβάση του $A$ είναι κάθε βάση του συνόλου όλων των διανυσμάτων που αποτελείται απο γραμμικά ανεξάρτητα ιδιοδιανύσματα του $A$. Ενας πίνακας με στοιχεία πραγματικούς αριθμούς μπορεί να μην έχει καμία ιδιοτιμή, αλλά ένας πίνακας με στοιχεία μιγαδικούς αριθμούς, έχει πάντα τουλάχιστον μία μιγαδική ιδιοτιμή.

Οι όροι χαρακτηριστικό διάνυσμα, χαρακτηριστικη τιμή, και χαρακτηριστικός χώρος χρησιμοποιούνται και σε αυτές τις έννοιες.

Οι ιδιοτιμές και τα ιδιοδιανύσματα έχουν πολλές εφαρμογές και στα θεωρητικά, αλλά και στα εφαρμοσμένα μαθηματικά. Χρησιμοποιούνται στην παραγοντοποίηση πινάκων, στην Κβαντική μηχανική, και σε πολλούς άλλους τομείς.

Ορισμός

Ιδιοδιανύσματα και ιδιοτιμές ενός πραγματικού πίνακα

Ο πίνακας $A$ απλά "τεντώνει" το διάνυσμα $x$, χωρίς να αλλάζει την κατεύθυνσή του, επομένως το $x$ είναι ένα ιδιοδιάνυσμα του $A$.

Σε πολλά περιβάλλοντα, ένα διάνυσμα μπορεί να θεωρηθεί σαν μία λίστα με πραγματικούς αριθμούς (που ονομάζονται "στοιχεία"), γραμμένους κάθετα με παρενθέσεις γύρω από όλη τη λίστα, όπως τα διανύσματα "u" και "v" παρακάτω. Λέμε ότι δύο διανύσματα είναι γραμμικά εξαρτημένα μεταξύ τους, όταν έχουν το ίδιο πλήθος στοιχείων, και κάθε στοιχείο του ενός διανύσματος προκύπτει αν πολλαπλασιάσουμε το αντίστοιχο στοιχείο του άλλου διανύσματος, με ένα σταθερό αριθμό (γνωστό και ως "γραμμικό συντελεστή"). Για παράδειγμα, τα διανύσματα

$u={\begin{bmatrix}1\\3\\4\end{bmatrix}}\quad \quad \quad$ και $\quad \quad \quad v={\begin{bmatrix}-20\\-60\\-80\end{bmatrix}}$

είναι γραμμικά εξαρτημένα μεταξύ τους, αφού κάθε στοιχείο του $v$ είναι -20 φορές το στοιχείο στην αντίστοιχη θέση του $u$.

Ενα διάνυσμα με 3 στοιχεία, όπως το $u$ ή το $v$ παραπάνω, μπορεί να αντιπροσωπεύουν ένα σημείο σε ένα τρισδιάστατο χώρο, αντιστοιχίζοντας το με Καρτεσιανές συντεταγμένες. Μας βοηθάει να σκεφτούμε τέτοια διανύσματα ως τη μύτη ενός βέλους, η αρχή του οποίου βρίσκεται στην αρχή των αξόνων του συστήματος συντεταγμένων. Σ'αυτη την περίπτωση, η συνθήκη "το $u$ είναι παράλληλο με το $v$" σημαίνει ότι τα δύο βέλη κείτονται στην ίδια εύθεια γραμμή, και μπορεί να διαφέρουν μόνο στο μήκος και τη φορά, κατά μήκος της ευθείας αυτής.

Αν πολλαπλασιάσουμε οποιονδήποτε τετραγωνικό πίνακα $A$ με $n$ γραμμές και $n$ στήλες με ένα τέτοιο διάνυσμα $v$, το αποτέλεσμα θα είναι ένα νέο διάνυσμα $w=Av$, επίσης με $n$ γραμμές και μία στήλη. Ετσι έχουμε

${\begin{bmatrix}v_{1}\\v_{2}\\\vdots \\v_{n}\end{bmatrix}}\quad \quad$ αντιστοιχεί στο ${\begin{bmatrix}w_{1}\\w_{2}\\\vdots \\w_{n}\end{bmatrix}}\;=\;{\begin{bmatrix}A_{1,1}&A_{1,2}&\ldots &A_{1,n}\\A_{2,1}&A_{2,2}&\ldots &A_{2,n}\\\vdots &\vdots &\ddots &\vdots \\A_{n,1}&A_{n,2}&\ldots &A_{n,n}\\\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\\\vdots \\v_{n}\end{bmatrix}}$

όπου, για κάθε δείκτη $i$,

$w_{i}=A_{i1}v_{1}+A_{i2}v_{2}+\cdots +A_{in}v_{n}=\sum _{j=1}^{n}A_{ij}v_{j}$

Γενικά, αν το $v$ δεν είναι το μηδενικό διάνυσμα, τα διανύσματα $v$ και $Av$ δε θα είναι παράλληλα. Οταν "είναι" παράλληλα (δηλαδή όταν υπάρχει πραγματικός αριθμός $\lambda$ τέτοιος ώστε $Av=\lambda v$) λέμε ότι το $v$ είναι ένα ιδιοδιάνυσμα του $A$. Σ'αυτη την περίπτωση, ο γραμμικός συντελεστής $\lambda$ ορίζεται να είναι η ιδιοτιμή που αντιστοιχεί σ'αύτο το ιδιοδιάνυσμα.

Συγκεκριμένα, πολλαπλασιασμός με έναν 3x3 πίνακα $A$ μπορεί να αλλάξει και την κατεύθυνση και το μέγεθος ενός βέλους $v$ στον τρισδιάστατο χώρο. Παρολαυτά, αν $v$ είναι ένα ιδιοδιάνυσμα του $A$ με ιδιοτιμή $\lambda$, η διαδικασία μπορει να αλλάξει μόνο το μήκος του ή να αναστρέψει τη φορά του (να κάνει το βέλος να δείχνει στην ακριβώς αντίθετη κατεύθυνση). Συγκεκριμένα, το μήκος του βέλους θα αυξηθεί αν $|\lambda |>1$, θα παραμείνει ίδιο αν $|\lambda |=1$, και θα μειωθεί αν $|\lambda |<1$. Επιπλέον, η κατεύθυνση θα παραμείνει η ίδια αν $\lambda >0$, και θα αναστραφεί, αν $\lambda <0$. Αν $\lambda =0$, το μήκος του βέλους γίνεται μηδέν.

Ενα παράδειγμα

Ο πίνακας μετασχηματισμού ${\bigl [}{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}{\bigr ]}$ διατηρεί την κατεύθυνση των διανυσμάτων που είναι παράλληλα στο ${\bigl [}{\begin{smallmatrix}1\\1\end{smallmatrix}}{\bigr ]}$ (σε μπλε) και ${\bigl [}{\begin{smallmatrix}1\\-1\end{smallmatrix}}{\bigr ]}$ (σε μωβ). Τα σημεία που κείτονται στη βασική ευθεία, παράλληλη σε ένα ιδιοδιάνυσμα, παραμένουν στην ευθεία αυτή και μετά τον μετασχηματισμό. Τα διανύσματα με κόκκινο δεν είναι ιδιοδιανύσματα, επομένως η κατεύθυνση τους αλλάζει από το μετασχηματισμό. Δείτε επίσης: Μια επεκτεταμένη έκδοχη, που δείχνει και τα 4 τεταρτοκύκλια.

Για τον πίνακα μετασχηματισμού

$A={\begin{bmatrix}3&1\\1&3\end{bmatrix}},$

το διάνυσμα

$v={\begin{bmatrix}4\\-4\end{bmatrix}}$

είναι ένα ιδιοδιάνυσμα με ιδιοτιμή 2. Πράγματι,

$Av={\begin{bmatrix}3&1\\1&3\end{bmatrix}}{\begin{bmatrix}4\\-4\end{bmatrix}}={\begin{bmatrix}3\cdot 4+1\cdot (-4)\\1\cdot 4+3\cdot (-4)\end{bmatrix}}$

$={\begin{bmatrix}8\\-8\end{bmatrix}}=2\cdot {\begin{bmatrix}4\\-4\end{bmatrix}}.$

Αντίθετα, το διάνυσμα

$v={\begin{bmatrix}0\\1\end{bmatrix}}$

δεν είναι ένα ιδιοδιάνυσμα, αφού

${\begin{bmatrix}3&1\\1&3\end{bmatrix}}{\begin{bmatrix}0\\1\end{bmatrix}}={\begin{bmatrix}3\cdot 0+1\cdot 1\\1\cdot 0+3\cdot 1\end{bmatrix}}={\begin{bmatrix}1\\3\end{bmatrix}},$

και αυτό το διάνυσμα δεν είναι πολλαπλάσιο του αρχικού διανύσματος $v$.

Αλλο ένα παράδειγμα

Για τον πίνακα

$A={\begin{bmatrix}0&1&0\\0&2&0\\0&0&3\end{bmatrix}},$

έχουμε

$A{\begin{bmatrix}1\\0\\0\end{bmatrix}}={\begin{bmatrix}0\\0\\0\end{bmatrix}}=0\cdot {\begin{bmatrix}1\\0\\0\end{bmatrix}},\quad \quad$

$A{\begin{bmatrix}0\\0\\1\end{bmatrix}}={\begin{bmatrix}0\\0\\3\end{bmatrix}}=3\cdot {\begin{bmatrix}0\\0\\1\end{bmatrix}},\quad \quad$ και

$A{\begin{bmatrix}1\\2\\0\end{bmatrix}}={\begin{bmatrix}2\\4\\0\end{bmatrix}}=2\cdot {\begin{bmatrix}1\\2\\0\end{bmatrix}}.$

Επομένως, τα διανύσματα $[1,0,0]^{\top }$, $[0,0,1]^{\top }$ και $[1,2,0]^{\top }$ είναι ιδιοδιανύσματα του $A$ που αντιστοιχούν στις ιδιοτιμές 0, 3, και 2, αντίστοιχα. (Εδώ το σύμβολο ${}^{\top }$ δηλώνει την αναστροφή πίνακα, στην προκειμένη περίπτωση, μετατρέποντας τα διανύσματα-γραμμές, σε διανύσματα-στήλες.)

Τετριμμένες περιπτώσεις

Ο ταυτoτικός πίνακας $I$ (όπου το τυχαίο σημείο του $I_{ij}$ είναι 1 αν $i=j$, και 0 σε κάθε άλλη περίπτωση) αντικατοπτρίζει κάθε διάνυσμα στον εαυτό του. Έτσι κάθε διάνυσμα είναι ένα ιδιοδιάνυσμα του $I$, με ιδιοτιμή 1.

Γενικότερα, αν ο $A$ είναι ένας διαγώνιος πίνακας (με $A_{ij}=0$ όταν $i\neq j$), και $v$ ένα διάνυσμα παράλληλο στον άξονα $i$ (το οποίο είναι $v_{i}\neq 0$, και $v_{j}=0$ αν $j\neq i$), τότε $Av=\lambda v$ όπου $\lambda =A_{ii}$. Δηλαδή, οι ιδιοτιμές ενός διαγώνιου πίνακα είναι τα στοιχεία της κύριας διαγωνίου του. Αυτή είναι τετριμμένα και η περίπτωση ενός οποιουδήποτε 1 ×1 πίνακα

Γενικός ορισμός

Η έννοια των ιδιοτιμών και των ιδιοδιανυσμάτων επεκτείνεται φυσικά σε αόριστους γραμμικούς μετασχηματισμούς σε αόριστους ιδιοχώρους. Ονομαστικά, ας είναι $\mathbb {V}$ οποιοσδήποτε ιδιοχώρος μέσα σε μία πεδίο $\mathbb {K}$ τών μονοδιάστατων, και ας είναι $T$ μια χαρτογράφηση γραμμικού μετασχηματισμού $\mathbb {V}$ σε $\mathbb {V}$. Λέμε πως ένα μη μηδενικό διάνυσμα $v$ ενός $\mathbb {V}$ είναι ένα ιδιοδιάνυσμα του $T$ αν(και μόνο αν) υπάρχει ένα μονοδιάστατο $\lambda$ σε $\mathbb {K}$ έτσι ώστε

$T(v)=\lambda v$.

Αυτή η εξίσωση καλείται εξίσωση ιδιοτιμής για το $T$, και το μονοδιάστατο $\lambda$ είναι η ιδιοτιμή του $T$ που αντιστοιχεί στο διάνυσμα $v$. Το $T(v)$ είναι το αποτέλεσμα της εφαρμογής του $T$ στο διάνυσμα $v$, ενώ $\lambda v$ το αποτέλεσμα του μοναδιαίου $\lambda$ στο $v$. Ο ορισμός για τους πίνακες είναι μια ειδική περίπτωση αυτού του γενικού ορισμού. Ονομαστικά ο ιδιοχώρος $\mathbb {V}$ είναι το σύνολο όλων των διανυσμάτων στηλών μιας συγκεκριμένης διάστασης $n$×1, και $T$ είναι ένας γραμμικός μετασχηματισμός που συνίσταται στoν πολλαπλασιασμό $n\times n$ ενός διανύσματος με τον δοσμένο πίνακα $A$.

Μερικοί συντάκτες επιτρέπουν στο $v$ να είναι το μηδενικό διάνυσμα στον ορισμό του ιδιοδιανύσματος. Κάτι τέτοιο είναι λογικό εφόσον ορίσουμε προσεκτικά τις ιδιοτιμές και τα ιδιοδιανύσματα: Αν θέλουμε να συμπεριλάβουμε στον ορισμό το μηδενικό διάνυσμα ώς ιδιοδιάνυσμα, πρέπει πρώτα να ορίσουμε μια ιδιοτιμή του $T$ ώς ένα μοναδιαίο $\lambda$ σε $\mathbb {K}$ έτσι ώστε να υπάρχει ένα μη μηδενικό διάνυσμα $v$ σε $\mathbb {V}$ με $Tv=\lambda v$. Όταν ορίζουμε ένα ιδιοδιάνυσμα να είναι ένα διάνυσμα $v$ σε $\mathbb {V}$ έτσι ώστε να υπάρχει μια ιδιοτιμή $\lambda$ σε $\mathbb {K}$ με $Tv=\lambda v$. Με αυτόν τον τρόπο βεβαιώνουμε πως δεν είμαστε στην περίπτωση που κάθε ιδιοτιμή αντιστοιχεί στο μηδενικό διάνυσμα.

Ιδιοχώρος και φάσμα

Αν το $v$ είναι ένα ιδιοδιάνυσμα του $T$, με ιδιοτιμή $\lambda$, τότε κάθε γραμμικός συνδυασμός $\alpha v$ του $v$ με $\alpha$ μη μηδενικό, είναι επίσης ένα ιδιοδιάνυσμα με ιδιοτιμή $\lambda$, αφού $T(\alpha v)=\alpha T(v)=\alpha (\lambda v)=\lambda (\alpha v)$. Επιπλέον, αν τα $u$ και $v$ είναι ιδιοδιανύσματα με την ίδια ιδιοτιμή $\lambda$, τότε το $u+v$ είναι επίσης ένα ιδιοδιάνυσμα με την ίδια ιδιοτιμή $\lambda$. Επομένως, το σύνολο όλων των ιδιοδιανυσμάτων με την ίδια ιδιοτιμή $\lambda$, συμπεριλαμβανομένου του μηδενικού διανύσματος, είναι ένας γραμμικός υποχώρος του $\mathbb {V}$, που ονομάζεται ιδιοχώρος του $T$ με παράμετρο $\lambda$. Αν ο υποχώρος αυτός έχει διάσταση 1, τότε συνήθως ονομάζεται ιδιογραμμή.

Ο γεωμετρικός πολλαπλασιαστής $\gamma _{T}(\lambda )$ μιας ιδιοτιμής $\lambda$ είναι η διάσταση του ιδιοχώρου με παράμετρο $\lambda$, π.χ. ο αριθμός των γραμμικά ανεξάρτητων ιδιοδιανυσμάτων με αυτή την ιδιοτιμή. Αυτά τα ιδιοδιανύσματα, μπορούν να επιλεγούν με τέτοιο τρόπο ώστε να είναι κατά ζεύγη ορθογώνια και να έχουν μήκος μονάδας κάτω από κάποιο αυθαίρετο εσωτερικό γινόμενο ορισμένο στον $\mathbb {V}$. Με άλλα λόγια, κάθε ιδιοχώρος έχει μια ορθοκανονική βάση αποτελούμενη από ιδιοδιανύσματα.

Αντίστροφα, κάθε ιδιοδιάνυσμα με ιδιοτιμή $\lambda$ πρέπει να είναι γραμμικά ανεξάρτητο με όλα τα ιδιοδιανύσματα που είναι συνδεδεμένα με μια διαφορετική ιδιοτιμή $\lambda '$. Επομένως, ο γραμμικός μετασχηματισμός $T$ που εφαρμόζεται σε ένα $n$-διάστατο χώρο δεν μπορεί να έχει παραπάνω από $n$ σαφείς ιδιοτιμές (ή ιδιοχώρους).

Κάθε υποχώρος που παράγεται από ιδιοδιανύσματα του $T$ είναι ένας αμετάβλητος υποχώρος του $T$.

Το σύνολο των ιδιοτιμών του $T$ ονομάζεται μερικές φορες το φάσμα του $T$. Η σειρά αυτού του συνόλου είναι αυθαίρετη, αλλά το πλήθος των φορών που εμφανίζεται μια ιδιοτιμή $\lambda$ είναι σημαντικό.

Δεν υπάρχει μοναδικός τρόπος να διαλέξουμε μια βάση για έναν ιδιοχώρο ενός αυθαίρετου γραμμικού τελεστή $T$ που να βασίζεται μόνο στον $T$, χωρίς κάποια επιπλέον στοιχεία, όπως η επιλογή της βάσης συντεταγμένων του $\mathbb {V}$. Ακόμη και για μια ιδιογραμμή, το διάνυσμα της βάσης είναι ασαφές και ως προς το μέγεθος, και ως προς την κατεύθυνσή του. Αν ο βαθμωτός χώρος $\mathbb {K}$ είναι ο χώρος των πραγματικών αριθμών $\mathbb {R}$, τότε μπορουμε να ορίσουμε τους ιδιοχώρους από τις ιδιοτιμές. Αφου το μόντουλο $|\lambda |$ μιας ιδιοτιμής είναι σημαντικό σε πολλές εφαρμογές, οι ιδιοχώροι συχνά ορίζονται με αυτό το κριτήριο.

Ιδιοβάση

Μια ιδιοβάση ενός γραμμικού τελεστή $T$ που εφαρμόζεται σε ένα διανυσματικό χώρο $\mathbb {V}$ είναι μια βάση του $\mathbb {V}$ που αποτελείται εξ'ολοκλήρου από ιδιοδιανύσματα του $T$ (πιθανότατα με διαφορετικές ιδιοτιμές). Τετοιού είδους βάση μπορεί και να μην υπάρχει.

Ας υποθέσουμε ότι ο $\mathbb {V}$ έχει πεπερασμένη διάσταση $n$, και ας θέσουμε ${\boldsymbol {\gamma }}_{T}$ το άθροισμα των γεωμετρικών πολλαπλάσιων $\gamma _{T}(\lambda _{i})$ πάνω σε όλες τις ανεξάρτητες ιδιοτιμές $\lambda _{i}$ του $T$. Ο ακέραιος αυτός είναι ο μέγιστος αριθμός των γραμμικά ανεξάρτητων ιδιοδιανυσμάτων του $T$, κι επομένως δεν μπορεί να είναι μεγαλύτερος του $n$. Αν το ${\boldsymbol {\gamma }}_{T}$ είναι ακριβώς $n$, τότε ο $T$ ορίζει μια ιδιοβάση, με προϋπόθεση ότι υπάρχει μια βάση του $\mathbb {V}$ που αποτελείται από $n$ ιδιοδιανύσματα. Ο πίνακας $A$ που αντιπροσωπεύει τον $T$ ως προς τη βάση αυτή, είναι ένας διαγώνιος πίνακας, του οποίου τα διαγώνια στοιχεία είναι οι ιδιοτιμές που αντιστοιχούν σε κάθε διάνυσμα της βάσης αυτής.

Αντίθετα, αν το άθροισμα ${\boldsymbol {\gamma }}_{T}$ είναι μικρότερο του $n$, τότε ο $T$ δεν ορίζει ιδιοβάση, και δεν υπάρχει κατάλληλη επιλογή συντεταγμένων, τέτοιες ώστε να επιτρέψουν τον $T$ να αντικατασταθεί από ένα διαγώνιο πίνακα.

Ο ${\boldsymbol {\gamma }}_{T}$ είναι τουλάχιστον ίσος με το πλήθος των ανεξάρτητων ιδιοτιμών του $T$, αλλά μπορεί να είναι και μεγαλύτερος απ'αυτό. Για παράδειγμα, ο φορέας ταυτότητας $I$ στον $\mathbb {V}$ έχει ${\boldsymbol {\gamma }}_{I}=n$, και κάθε βάση του $\mathbb {V}$ είναι μια ιδιοβάση του $I$; αλλά η μόνη της ιδιοτιμή είναι το 1, με $\gamma _{T}(1)=n$.

Γενικεύσεις σε άπειρο-διάστατους χώρους

Ο ορισμός μιας ιδιοτιμής ενός γραμμικού μετασχηματισμού $T$ μένει έγκυρος ακόμη και όταν ο χώρος $\mathbb {V}$ είναι ένας απειροδιαστατος χώρος Χίλμπερτ ή Μπανάχ. Ονομαστικά, ένα μονοδιάστατο $\lambda$ αν και μόνο αν υπάρχει ενα μη μηδενικό διάνυσμα $v$ τέτοιο ώστε $T(v)=\lambda v$.

Ιδιοσυναρτήσεις

Μια ευρέως χρησιμοποιούμενη κλάση γραμμικών τελεστών πάνω σε απειροδιάστατους χώρους είναι οι διαφορικοί τελεστές σε χώρους συναρτήσεων. Ας είναι $D$ ένας γραμμικός διαφορικός τελεστής σε έναν χώρο $\mathbf {C^{\infty }}$ απειροπαραγωγίσιμων πραγματικών συναρτήσεων, πραγματικού συντελεστή $t$. Η εξίσωση των ιδιοδιανυσμάτων του $D$ είναι η διαφορική εξίσωση

$Df=\lambda f$

Οι συναρτήσεις που ικανοποιούν την εξίσωση συνήθως καλούνται ιδιοσυναρτήσεις. Για τον διαφορικό τελεστή $d/dt$, μια ιδιοσυνάρτηση είναι μια συνάρτηση η οποία, όταν παραγωγιστεί, αποδίδει την αρχική επί μία σταθερά. Αν $\lambda$ είναι μηδέν, η γενική λύση είναι μια σταθερή συνάρτηση. Αν το $\lambda$ είναι μη μηδενικό, η λύση είναι μια εκθετική συνάρτηση

$f(t)=Ae^{\lambda t}.\$

Οι ιδιοσυναρτήσεις είναι ένα κύριο εργαλείο για την επίλυση διαφορικών εξισώσεων και πολλών ακόμα εφαρμοσμένων και θεωρητικών πεδίων. Για παράδειγμα οι εκθετικές συναρτήσεις είναι ιδιοσυναρτήσεις ενός οποιουδήποτε μετατοπιστικά αμετάβλητου γραμμικού τελεστή. Το γεγονός αυτό είναι η βάση των ισχυρότατων μεθόδων μετασχηματισμού Φουριέ για την επίλυση προβλημάτων όλων των ειδών.

Φασματική θεωρία

Αν $\lambda$ είναι μια ιδιοτιμή του $T$, τότε ο τελεστής $T-\lambda I$ δεν είναι ένα προς ένα, και έτσι το αντίστροφό του $(T-\lambda I)^{-1}$ δεν ορίζεται. Το αντίστροφο ισχύει για πεπερασμένης διάστασης διανυσματικούς χώρους, αλλά όχι για απειροδιάστατους. Γενικά ο τελεστής $T-\lambda I$ δεν έχει αντίστροφο, ακόμη και όταν το $\lambda$ δεν είναι ιδιοτιμή.

Για αυτόν τον λόγο στη συναρτησιακή ανάλυση το ένα ορίζει το φάσμα ενός γραμμικού τελεστή $T$ ώς σύνολο όλων των μονοδιάστατων $\lambda$ για τα οποία ο τελεστής $T-\lambda I$ δεν έχει οριοθετημένο αντίστροφο. Έτσι το φάσμα ενός τελεστή πάντα περιέχει όλες τις ιδιοτιμές, αλλά δεν περιορίζεται σε αυτές.

Άλγεβρες συσχετισμού και θεωρία αναπαράστασης

Πιο αλγεβρικά αντί να γενικεύσουμε τον διανυσματικό χώρο σε έναν απειροδιάστατο χώρο, μπορούμε να γενικεύσουμε το αλγεβρικό αντικείμενο που δρα στον χώρο, αντικαθιστώντας έναν μονοδιάστατο τελεστή που δρα στον διανυσματικό χώρο με μια άλγεβρα αναπαράστασης - μια άλγεβρα συσχετισμού που δρα σε μία μονάδα.Η μελέτη αυτών των φαινομένων είναι το πεδίο μελέτης της θεωρίας αναπαράστασης.

Ενα καλύτερο ανάλογο των ιδιοτιμών δίνεται από τη θεωρητική-αναπαραστασιακή έννοια του βάρους, με τα ανάλογα των ιδιοτιμών και ιδιοχώρων να είναι τα διανύσματα βάρους και οι χώροι βάρους αντίστοιχα.

Ιδιοτιμές και ιδιοδιανύσματα πινάκων

Χαρακτηριστικό πολυώνυμο

Η εξίσωση ιδιοτιμής για έναν πίνακα $A$ είναι

$Av=\lambda v,$

που είναι ισοδύναμο με

$(A-\lambda I)v=0,$

όπου $I$ είναι ο $n\times n$ ταυτοτικός πίνακας. Είναι ένα θεμελιώδες αποτέλεσμα της γραμμικής αλγέβρας ότι μια εξίσωση $Mv=0$ έχει μια μη μηδενική λύση $v$ αν και μόνο αν η ορίζουσα $\det(M)$ του πίνακα $M$ είναι μηδέν. Αμεσο επακόλουθο είναι ότι οι ιδιοτιμές του πίνακα $A$ είναι ακριβώς οι πραγματικοί αριθμοί $\lambda$ που ικανοποιούν την εξίσωση

$\det(A-\lambda I)=0$

Το αριστερό μέλος αυτής της εξίσωσης μπορούμε να το δούμε (χρησιμοποιώντας τον κανόνα Leibniz για την ορίζουσα) ως μία πολυωνυμική συνάρτηση της μεταβλητής $\lambda$. Ο βαθμός του πολυωνύμου αυτού, είναι $n$, όσο και η τάξη του πίνακα. Οι συντελεστές του εξαρτώνται απο τις εκχωρήσεις στον $A$, με μόνη διαφορά ότι ο όρος βαθμού $n$ είναι πάντα $(-1)^{n}\lambda ^{n}$. Το πολυώνυμο αυτό ονομάζεται Χαρακτηριστικό πολυώνυμο του $A$ και η παραπάνω εξίσωση, χαρακτηριστική εξίσωση (ή, πιο σπάνια, η κοσμική εξίσωση) του $A$.

Για παράδειγμα, ας είναι $A$ ο πίνακας

$A={\begin{bmatrix}2&0&0\\0&3&4\\0&4&9\end{bmatrix}}$

Το χαρακτηριστικό πολυώνυμο του $A$ είναι

$\det(A-\lambda I)\;=\;\det \left({\begin{bmatrix}2&0&0\\0&3&4\\0&4&9\end{bmatrix}}-\lambda {\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}\right)\;=\;\det {\begin{bmatrix}2-\lambda &0&0\\0&3-\lambda &4\\0&4&9-\lambda \end{bmatrix}}$

που είναι

$(2-\lambda ){\bigl [}(3-\lambda )(9-\lambda )-16{\bigr ]}=\lambda ^{3}-14\lambda ^{2}+35\lambda -22$

Οι ρίζες του πολυωνύμου αυτού είναι 2, 1, και 11. Πράγματι, αυτές οι τρεις είναι οι μόνες ιδιοτιμές του $A$, που αντιστοιχούν στα ιδιοδιανύσματα $[1,0,0]',$ $[0,2,-1]',$ και $[0,1,2]'$ (ή κάθε μη μηδενικό πολλαπλάσιο τους).

Στον πραγματικό χώρο

Αφού οι ιδιοτιμές είναι οι ρίζες του χαρακτηριστικού πολυωνύμου, ένας $n\times n$ πίνακας, έχει το πολύ $n$ ιδιοτιμές. Αν ο πίνακας έχει πραγματικά στοιχεία, οι συντελεστές του χαρακτηριστικού πολυωνύμου είναι όλοι πραγματικοί αριθμοί, αλλά το πολύωνυμο μπορεί να έχει λιγότερες από $n$ πραγματικές ρίζες, ή καθόλου ρίζες.

Για παράδειγμα, ας θεωρήσουμε την κυκλική μετάθεση του πίνακα

$A={\begin{bmatrix}0&1&0\\0&0&1\\1&0&0\end{bmatrix}}$

Ο πίνακας αυτός αλλάζει τις συντεταγμένες οτυ διανύσματος κατά μία θέση προς τα πάνω, και μεταφέρει την πρώτη συντεταγμένη εντελώς κάτω. Το χαρακτηριστικό του πολυώνυμο, είναι $1-\lambda ^{3}$ που έχει μία πραγματική ρίζα $\lambda _{1}=1$. Κάθε διάνυσμα με τρία ίσα μη μηδενικά στοιχεία, είναι ένα ιδιοδιάνυσμα αυτής της ιδιοτιμής. Για παράδειγμα,

$A{\begin{bmatrix}5\\5\\5\end{bmatrix}}={\begin{bmatrix}5\\5\\5\end{bmatrix}}=1\cdot {\begin{bmatrix}5\\5\\5\end{bmatrix}}$

Στο μιγαδικό χώρο

Το θεμελιώδες θεώρημα της άλγεβρας μας λέει ότι το χαρακτηριστικό πολυώνυμο ενός $n\times n$ πίνακα $A$, όντας ένα πολυώνυμο βαθμού $n$, έχει ακριβώς $n$ μιγαδικές ρίζες. Ακριβέστερα, μπορεί να παραγονοποιηθεί σε $n$ γραμμικούς όρους,

$\det(A-\lambda I)=(\lambda _{1}-\lambda )(\lambda _{2}-\lambda )\cdots (\lambda _{n}-\lambda )$

όπου κάθε $\lambda _{i}$ είναι ένας μιγαδικός αριθμός. Οι αριθμοί $\lambda _{1}$, $\lambda _{2}$, ... $\lambda _{n}$, (που μπορεί να μην είναι όλοι ξεχωριστοί) είναι ρίζες του πολυωνύμου, και είναι ακριβώς οι ιδιοτιμές του $A$.

Ακόμα κι αν τα στοιχεία του $A$ είναι όλα πραγματικοί αριθμοί, οι ιδιοτιμές μπορεί ακόμα να έχουν μη μηδενικά φανταστικά μέρη (και τα στοιχεία των αντίστοιχων ιδιοδιανυσμάτων να έχουν επίσης μη μηδενικά φανταστικά μέρη). Επίσης, οι ιδιοτιμές μπορεί να είναι άρρητοι αριθμοί ακόμη κι αν όλα τα στοιχεία του $A$ είναι πραγματικοί αριθμοί, ή όλοι να είναι ακέραιοι. Παρόλαυτα, αν τα στοιχεία του $A$ είναι αλγεβρικοί αριθμοί (που περιλαμβάνουν τους ρητόυς αριθμούς), οι ιδιοτιμές θα είναι επίσης (μιγαδικοί) αλγεβρικοί αριθμοί.

Οι μη-πραγματικές ρίζες ενός πραγματικού πολυωνύμου με πραγματικούς συντελεστές μπορούν να ομαδοποιηθούν σε ζευγάρια συζυγών μιγαδικών, έτσι ώστε σε κάθε ζευγάρι, οι δυο αριθμοί να έχουν το ίδιο πραγματικό μέρος, και αντίθετα φανταστικά μέρη. Αν ο βαθμός του πολυωνύμου είναι περιττόες, τότε από το θεώρημα ενδιάμεσων τιμών τουλάχιστον μία από τις ρίζες θα είναι πραγματική. Επομένως, κάθε πραγματικός πίνακας με περιττή τάξη θα έχει τουλάχιστον μία πραγματική ιδιοτιμή, ένω ένας πραγματικός πίνακας με άρτια τάξη μπορεί να μην έχει πραγματικές ιδιοτιμές.

Στο παράδειγμα του 3×3 κυκλικού πίνακα μετάθεσης $A$ παραπάνω, το χαρακτηριστικό πολυώνυμο $1-\lambda ^{3}$ έχει δύο επιπρόσθετες μη-πραγματικές ρίζες, οι οποίες είναι

$\lambda _{2}=-1/2+\mathbf {i} {\sqrt {3}}/2\quad \quad$ και $\quad \quad \lambda _{3}=\lambda _{2}^{*}=-1/2-\mathbf {i} {\sqrt {3}}/2$,

όπου $\mathbf {i} ={\sqrt {-1}}$ είναι το φανταστικό μέρος. Να σημειωθεί ότι $\lambda _{2}\lambda _{3}=1$, $\lambda _{2}^{2}=\lambda _{3}$, και $\lambda _{3}^{2}=\lambda _{2}$. Τότε

$A{\begin{bmatrix}1\\\lambda _{2}\\\lambda _{3}\end{bmatrix}}={\begin{bmatrix}\lambda _{2}\\\lambda _{3}\\1\end{bmatrix}}=\lambda _{2}\cdot {\begin{bmatrix}1\\\lambda _{2}\\\lambda _{3}\end{bmatrix}}\quad \quad$ και $\quad \quad A{\begin{bmatrix}1\\\lambda _{3}\\\lambda _{2}\end{bmatrix}}={\begin{bmatrix}\lambda _{3}\\\lambda _{2}\\1\end{bmatrix}}=\lambda _{3}\cdot {\begin{bmatrix}1\\\lambda _{3}\\\lambda _{2}\end{bmatrix}}$

Επομένως, τα διανύσματα $[1,\lambda _{2},\lambda _{3}]'$ και $[1,\lambda _{3},\lambda _{2}]'$ είναι ιδιοδιανύσματα του $A$, με ιδιοτιμές 1, $\lambda _{2}$, και $\lambda _{3}$, αντίστοιχα.

Αλγεβρικές πολλαπλότητες

Ας είναι $\lambda _{i}$ μια ιδιοτιμή ενός $n\times n$ πίνακα $A$. Η αλγεβρική πολλαπλότητα $\mu _{A}(\lambda _{i})$ του $\lambda _{i}$ είναι η πολλαπλότητα του χαρακτηριστικου πολυωνύμου, η οποία είναι ο μεγαλύτερος ακέραιος αριθμός $k$ τέτοιος ώστε το $(\lambda -\lambda _{i})^{k}$ να διαιρεί τέλεια το πολυώνυμο αυτό.

Οπως και η γεωμετρική πολλαπλότητα $\gamma _{A}(\lambda _{i})$, η αλγεβρική πολλαπλότητα είναι ένας ακέραιος ανάμεσα στο 1 και το $n$, και το άθροισμα ${\boldsymbol {\mu }}_{A}$ του $\mu _{A}(\lambda _{i})$ πάνω απ'όλες τις ξεχωριστές ιδιοτιμές επίσης δεν μπορεί να είναι μεγαλύτερο του $n$. Αν ληφθούν υπ'όψιν και οι μιγαδικές ιδιοτιμές, το ${\boldsymbol {\mu }}_{A}$ είναι ακριβώς $n$.

Μπορεί να αποδειχθεί ότι η γεωμετρική πολλαπλότητα $\gamma _{A}(\lambda _{i})$ μιας ιδιοτιμής, ποτέ δεν μπορεί να είναι μεγαλύτερη της αλγεβρικής πολλαπλότητας $\mu _{A}(\lambda _{i})$. Επομένως, το ${\boldsymbol {\gamma }}_{A}$ είναι το πολύ ${\boldsymbol {\mu }}_{A}$.

Παράδειγμα

Για τον πίνακα: $A={\begin{bmatrix}2&0&0&0\\1&2&0&0\\0&1&3&0\\0&0&1&3\end{bmatrix}},$

το χαρακτηριστικό πολυώνυμο του $A$ είναι $\det(A-\lambda I)\;=\;\det {\begin{bmatrix}2-\lambda &0&0&0\\1&2-\lambda &0&0\\0&1&3-\lambda &0\\0&0&1&3-\lambda \end{bmatrix}}=(2-\lambda )^{2}(3-\lambda )^{2}$,

όντας το παράγωγο του διαγώνιου και ενός κάτω τριγωνικού πίνακα

Οι ρίζες αυτού του πολυωνύμου, και κατά συνέπεια και οι ιδιοτιμές του, είναι 2 και 3 Η αλγεβρική πολλαπλότητα κάθε ιδιοτιμής είναι 2, με άλλα λόγια είναι και οι δυο διπλές ρίζες. Από την άλλη, η γεωμετρική πολλαπλότητα της ιδιοτιμής 2 είναι μόνο 1, αφού ο ιδιοχώρος του παράγεται από το διάνυσμα $[0,1,-1,1]$, και είναι συνεπώς μονοδιάστατος. Παρομοίως, η γεωμετρική πολλαπλότητα της ιδιοτιμής 3 είναι 1 επειδή ο ιδιοχώρος του παράγεται από το $[0,0,0,1]$. Επομένως, η ολική αλγεβρική πολλαπλότητα του A,(σύμβολο $\mu _{A}$), είναι 4, το οποίο είναι το μέγιστο που θα μπορούσε να είναι, για έναν 4x4 πίνακα. Η γεωμετρική πολλαπλότητα $\gamma _{A}$ είναι 2, που είναι το ελάχιστο που θα μπορούσε να είναι για έναν πίνακα με 2 ξεχωριστές ιδιοτιμές.

Διαγωνιοποίηση και ιδιοαποσύνθεση

Αν το σύνολο ${\boldsymbol {\gamma }}_{A}$ της γεωμετρικής πολλαπλότητας όλων των ιδιοτιμών είναι ακριβώς $n$, τότε ο $A$ έχει ένα σύνολο $n$ γραμμικά ανεξάρτητων ιδιοδιανυσμάτων. Ας είναι $Q$ ένας τετράγωνος πινάκας του οποίου οι στήλες είναι αυτά τα ιδιοδιανύσματα, σε οποιαδήποτε σείρα. Έπειτα θα έχουμε $AQ=Q\Lambda$, όπου $\Lambda$ είναι ο διαγώνιος πίνακας τέτοιος ώστε $\Lambda _{ii}$ να είναι η ιδιοτιμη που αντιστοιχεί στη στήλη $i$ του $Q$. Εφόσον οι στήλες του $Q$ είναι γραμμικά ανεξάρτητες, ο πίνακας $Q$ είναι αντιστρέψιμος. Πολαπλασιάζοντας και από τις δύο πλευρές $Q^{-1}$ παίρνουμε $Q^{-1}AQ=\Lambda$. Εξ' ορισμού, ο πίνακας $A$ είναι διαγωνιοποιήσιμος.

Αντίστροφα, αν ο $A$ είναι διαγωνιοποιήσιμος, ας είναι $Q$ ενας μη μοναδιαίος τετραγωνικός πίνακας, τέτοιος ώστε ο $Q^{-1}AQ$ να είναι κάποιος διαγώνιος πίνακας $D$. Πολλαπλασιάζοντας και απο τις δύο πλευρές, στα αριστερά με τον $Q$ παίρνουμε $AQ=QD$. Ετσι, κάθε στήλη του $Q$ είναι ένα ιδιοδιάνυσμα του $A$, του οποίου η ιδιοτιμή είναι το αντίστοιχο στοιχείο του διαγώνιου $D$. Εφόσον οι στήλες $Q$ πρέπει να είναι γραμμικά ανεξάρτητες, έπεται ότι ${\boldsymbol {\gamma }}_{A}=n$. Προκύπτει λοιπόν πως ${\boldsymbol {\gamma }}_{A}$ είναι ίσο με $n$ αν και μόνο αν $A$ είναι διαγωνιοποιήσιμος.

Αν $A$ είναι διαγωνιοποιήσιμος, ο χώρος όλων των $n$-στοιχείων διανυσμάτων μπορεί να αποσυντεθεί στο ευθύ άθροισμα των ιδιοχώρων του $A$. Αυτή η αποσύνθεση καλείται ιδιοαποσύνθεση ενός πίνακα $A$, και μένει αναλλοίωτη στις αλλαγές συντεταγμένων.

Ένας μη διαγωνιοποιήσιμος πίνακας λέγεται ελαττωματικός. Για ελαττωματικούς πίνακες, η έννοια του ιδιοδιανύσματος μπορεί να γενικευτεί σε γενικευμένα ιδιοδιανύσματα, και αυτά ενος διαγώνιου σε έναν Τζόρνταν μορφής πίνακα. Σε ένα αλγεβρικά κλειστό πεδίο, κάθε πίνακας $A$ έχει Τζόρνταν μορφή και έτσι συμμετέχει σε μία βάση γενικευμένων ιδιοδιανυσμάτων, και μία αποσύνθεση σε έναν γενικευμένο ιδιοχώρο.

Επιπλέον ιδιότητες

Ας είναι $A$ ένας αυθαίρετος $n\times n$ πίνακας με μιγαδικά στοιχεία, και ιδιοτιμές $\lambda _{1}$, $\lambda _{2}$, ... $\lambda _{n}$. (Εδώ γίνεται κατανοητό ότι μια ιδιοτιμή με αλγεβρική πολλαπλότητα $\mu$ εμφανίζεται $\mu$ φορές στο σύνολο αυτο.) Τότε,

• Το ίχνος του $A$, ορισμένο ως το άθροισμα των στοιχείων της κύριας διαγωνίου του, είναι επίσης το άθροισμα όλων των ιδιοτιμών:

$\operatorname {tr} (A)=\sum _{i=1}^{n}A_{ii}=\sum _{i=1}^{n}\lambda _{i}=\lambda _{1}+\lambda _{2}+\cdots +\lambda _{n}$.

• Η ορίζουσα του $A$ είναι το γινόμενο όλων των ιδιοτιμών:

$\operatorname {det} (A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}$.

• Οι ιδιοτιμές της $k$-στης δύναμης του $A$, δήλαδη οι ιδιοτιμές του $A^{k}$, για κάθε θετικό ακέραιο $k$, είναι $\lambda _{1}^{k},\lambda _{2}^{k},\dots ,\lambda _{n}^{k}$
• Ο πίνακας $A$ είναι αντιστρέψιμος αν και μόνο αν όλες οι ιδιοτιμές του $\lambda _{i}$ είναι μη μηδενικές.
• Αν ο $A$ είναι αντιστρέψιμος, τότε οι ιδιοτιμές του $A^{-1}$ είναι $1/\lambda _{1},1/\lambda _{2},\dots ,1/\lambda _{n}$
• Αν ο $A$ είναι ίσος με τον προσαρτημένο του, $A^{*}$ (με άλλα λόγια, αν ο $A$ είναι ερμιτιανός), τότε κάθε ιδιοτιμή του είναι πραγματική. Το ίδιο ισχύει και για κάθε συμμετρικό πραγματικό πίνακα. Αν ο $A$ είναι επίσης θετικά ορισμένος, θετικά ημιορισμένος, αρνητικά ορισμένος, ή αρνητικά ημιορισμένος, τοτέ κάθε ιδιοτιμή είναι θετική, μη αρνητική, αρνητική, ή μη θετική αντίστοιχα.
• Κάθε ιδιοτιμή ενός ενιαίου πίνακα, έχει απόλυτη τιμή $|\lambda |=1$.

Αριστερές και δεξιές ιδιοτιμές

Η χρήση των πινάκων που αποτελούνται από μία στήλη (αντί για μία σειρά) για να αντιπροσωπεύουν διανύσματα, είναι παραδοσιακή σε πολλούς κλάδους. Για το λόγο αυτό, η λέξη "ιδιοδιάνυσμα" σχέδον πάντα εκφράζει ένα δεξί ιδιοδιάνυσμα, δηλαδή ένα διάνυσμα στήλη που πρέπει να τοποθετηθεί δεξιά από τον πίνακα $A$ στη χαρακτηριστική εξίσωση.

$Av=\lambda v$.

Μπορεί επίσης να υπάρχουν διανύσματα-γραμμές τα οποία δεν μεταβάλλονται όταν τοποθετηθούν στα αριστερά ένος γινομένου με έναν τετράγωνο πίνακα $A$. Αυτά ικανοποιούν την εξίσωση

$uA=\lambda u$

Κάθε διάνυσμα $u$ με αυτή την ιδιοτητα, ονομάζεται αριστερό ιδιοδιάνυσμα του A.

Τα αριστερά ιδιοδιανύσματα του $A$ είναι ανάστροφα των δεξιών ιδιοδιανυσμάτων του ανάστροφου πίνακα $A^{\top }$, αφού η χαρακτηριστική τους εξίσωση είναι ισοδύναμη με

$A^{\top }u^{\top }=\lambda u^{\top }$

Επακόλουθο είναι ότι, αν ο $A$ είναι ερμιτιανός, τα αριστερά και δεξιά ιδιοδιανύσματα του είναι μιγαδικα συζυγής χώρος. Ειδικά, αν ο $A$ είναι ένας πραγματικός συμμετρικός πίνακας, είναι ίδιοι σε όλα εκτός από την αναστροφή.

Υπολογισμός

Υπολογισμός των ιδιοτιμών

Οι ιδιοτιμές ενός πίνακα $A$ μπορούν να προσδιοριστούν βρίσκοντας τις ρίζες του χαρακτηριστικού πολυωνύμου. Σαφείς αλγεβρικοί τύποι για τις ρίζες ενός πολυωνύμου υπάρχουν μόνο άν ο βαθμός του $n$ είναι 4 ή μικρότερος. Σύμφωνα με το θεώρημα Αμπέλ-Ρουφινί δεν υπάρχει γενικός, σαφής και ακριβής αλγεβρικός τύπος που να υπολογίζει τις ρίζες ενός πολυωνύμου βαθμού 5 ή μεγαλύτερου.

Προκύπτει ότι κάθε πολυώνυμο βαθμού $n$ είναι το χαρακτηριστικό πολυώνυμο κάποιου συνοδευτικού πίνακα τάξης $n$. Επομένως, για πίνακες τάξης 5 ή παραπάνω, οι ιδιοτιμές και τα ιδιοδιανύσματα δεν μπορούν να προκύψουν από έναν ειδικό αλγεβρικό τύπο, και πρέπει συνεπώς να υπολογιστούν με προσεγγιστικές μεθόδους.

Θεωρητικά, οι συντελεστές του χαρακτηριστικού πολυωνύμου μπορούν να υπολογιστούν ακριβώς, αφού είναι αθροίσματα γινομένων από στοιχεία πινάκων, και υπάρχουν αλγόριθμοι που μπορούν να βρουν όλες τις ρίζες ενός πολυωνύμου αυθαίρετου βαθμού με όση ακρίβεια ζητηθεί. Παρόλαυτα, η προσέγγιση αυτή δεν είναι εφικτή στην πράξη, επειδή οι συντελεστές θα επηρεάζονταν από αναπόφευκτα λάθη στρογγυλοποίησης, και οι ρίζες ενός πολυωνύμου μπορει να είναι μια εξαιρετικά ευαίσθητη συνάρτηση των συντελεστών. (Οπως για παράδειγμα το πολυώνυμο του Wilkinson).

Αποτελεσματικές, ακριβείς μέθοδοι υπολογισμού ιδιοτιμών και ιδιοδιανυσμάτων τυχαίων πινάκων δεν ήταν γνωστές, μέχρι την επινόηση του αλγορίθμου QR το 1961. Συνδυάζοντας τον μετασχηματισμό Χαουζχόλντερ με την LU αποσύνθεση, παίρνουμε αποτελέσματα σε έναν αλγόριθμο με καλύτερη σύγκλιση από τον αλγόριθμο QR. Για μεγάλους ερμιτιανούς αραιούς πίνακες, ο αλγόριθμος Λάνκζος είναι ένα παράδειγμα μιας αποτελεσματικής επαναληπτικής μεθόδου για να υπολογίσουμε ιδιοτιμές και ιδιοδιανύσματα, ανάμεσα σε αρκετές άλλες πιθανότητες.

Υπολογισμός των ιδιοδιανυσμάτων

Αν είναι γνωστή η (ακριβής) τιμή μιας ιδιοτιμής, το αντίστοιχο ιδιοδιάνυσμα μπορεί να βρεθεί υπολογίζοντας τις μη-μηδενικές λύσεις της εξίσωσης ιδιοτιμής, η οποίες μετατρέπονται σε ένα γραμμικό σύστημα εξισώσεων με γνωστούς συντελεστές. Για παράδειγμα, αν είναι γνωστό ότι το 6 είναι μια ιδιοτιμή του πίνακα

$A={\begin{bmatrix}4&1\\6&3\end{bmatrix}}$

μπορούμε να βρούμε α ιδιοδιανύσματά του λύνοντας την εξίσωση $Av=6v$, που είναι

${\begin{bmatrix}4&1\\6&3\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}=6\cdot {\begin{bmatrix}x\\y\end{bmatrix}}$

Αυτή η εξίσωση πινάκων είναι ισοδύναμη με δύο γραμμικές εξισώσεις

$\left\{{\begin{matrix}4x+{\ }y&{}=6x\\6x+3y&{}=6y\end{matrix}}\right.\quad \quad \quad$ το οποίο είναι ισοδύναμα $\left\{{\begin{matrix}-2x+{\ }y&{}=0\\+6x-3y&{}=0\end{matrix}}\right.$

Και οι δύο αυτές εξισώσεις απλοποιούνται στην $y=2x$. Έτσι, κάθε διάνυσμα της μορφής $[a,2a]'$, για κάθε μη-μηδενικό πραγματικό αριθμό $a$, είναι ένα ιδιοδιάνυσμα του $A$ με ιδιοτιμή $\lambda =6$.

Ο παραπάνω πίνακας $A$ έχει και μια άλλη ιδιοτιμή, την $\lambda =1$. Ένας παρόμοιος υπολογισμός δείχνει ότι τα αντίστοιχα ιδιοδιανύσματα είναι οι μη-μηδενικές λύσεις της $3x+y=0$, που είναι, οποιοδήποτε διάνυσμα τις μορφής $[b,-3b]'$, για κάθε πραγματικό αριθμό $b$.

Μερικές αριθμητικές μέθοδοι για τον υπολογισμό των ιδιοτιμών ενός πίνακα επίσης ορίζουν ένα σύνολο αντιστοίχων ιδιοδιανυσμάτων ως ένα παραπροϊόν του υπολογισμού.

Ιστορία

Οι ιδιοτιμές συνήθως συστήνονται μέσα από το περιεχόμενο της γραμμικής άλγεβρας ή της θεωρίας πινάκων. Αντιθέτως, ιστορικά, αναπτύχθηκαν με τη μελέτη των τετραγωνικών μορφών και των διαφορικών εξισώσεων.

Ο Όιλερ μελέτησε την περιστροφική κίνηση ενός άκαμπτου σώματος και ανακάλυψε τη σημασία των κύριων αξόνων. Ο Λαγκράνζ ανακάλυψε ότι οι κύριοι άξονες είναι ιδιοδιανύσματα του αδρανούς πίνακα. Στις αρχές του 19ου αιώνα, ο Κωσύ είδε πώς ή δουλεία τους θα μπορούσε να χρησιμοποιηθεί για να ταξινομήσει τις τετραγωνικές επιφάνειες, και το γενίκευσε σε αυθαίρετες διαστάσεις. Επίσης, ο Κωσύ επινόησε τον όρο racine caractéristique (χαρακτηριστική ρίζα) για αυτό που σήμερα εμείς ονομάζουμε ιδιοτιμή. Ο όρος του παραμένει και χρησιμοποιείται πλέον στη χαρακτηριστική εξίσωση.

Ο Φουριέ χρησιμοποίησε το έργο του Λαπλάς και του Λαγκρανζ για να λύσει την εξίσωση θερμότητας για διαχωρισμένες μεταβλητές στο διάσημο βιβλίο του από το 1822 Théorie analytique de la chaleur. Ο Στερμ ανέπτυξε παραπάνω τις ιδέες του Φουριε και της έφερε στην προσοχή του Κωσύ, ο οποίος τις συνδύασε με τις δικές του ιδέες και κατέληξε στο γεγονός ότι οι πραγματικοί συμμετρικοί πίνακες, έχουν πραγματικές ιδιοτιμές. Αυτό, επεκτάθηκε από τον Ερμίτ το 1855 σε αυτό που σήμερα ονομάζεται ερμιτιανός πίνακας. Περίπου την ίδια περίοδο, ο Μπριόσι, απέδειξε ότι οι ιδιοτιμές ενός ορθογώνιου πίνακα βασίζονται στο μοναδιαίο κύκλο, και ο Κλεμπς βρήκε το αντίστοιχο αποτέλεσμα για τους αντισυμμετρικούς πίνακες. Τελικά, ο Βάιερστρας διευκρίνισε μια σημαντική οπτική της θεωρίας της σταθερότητας ξεκινώντας απο τον Λαπλάς συνειδητοποιώντας ότι οι ελλιπείς πίνακες μπορούν να προκαλέσουν αστάθεια.

Εν τω μεταξύ, ο Λιουβίλ μελέτησε προβλήματα ιδιοτιμών παρόμοια με εκείνα του Στέρμ: ο κλάδος που προέκυψε από την δουλέια τους καλείται πλέον Θεωρία των Λιουβίλ-Στέρμ. Ο Σβαρτς μελέτησε την πρώτη ιδιοτιμή της Λαπλασιανής εξίσωσης σε γενικούς τομείς μέχρι το τέλος του 19ου αιώνα, ενώ ο Πουανκαρέ μελέτησε την εξίσωση του Πουασόν μερικά χρόνια μετά.

Στις αρχές του 20ου αιώνα, ο Χίλμπερτ μελέτησε τις ιδιοτιμές του ολοκληρωματικού τελεστή βλέποντας τους τελεστές σαν απειροδιάστατους πίνακες. Ήταν ο πρώτος που χρησιμοποίησε την γερμανική λέξη eigen για να δηλώσει τις ιδιοτιμές και τα ιδιοδιανύσματα το 1904, αν και ακολουθούσε ήδη μια σχετική ονομασία απο τον Χέλμχολντς. Για κάποιο χρονικό διάστημα, ο όρος που χρησιμοποιούνταν ήταν "κανονική τιμή"(proper value), αλλα ο πιό χαρακτηριστικός όρος "ιδιοτιμή"(eigenvalue) έχει επικρατήσει.

Ο πρώτος αριθμητικός αλγόριθμος για τον υπολογισμό των ιδιοτιμών και ιδιοδιανυσμάτων εμφανίστηκε το 1929, όταν ο βόν Μίσις εξέδωσε την μέθοδο τις κίνησης. Μία από τις πιο δημοφιλείς μεθόδους σήμερα είναι, Ο QR αλγόριθμος, που προτάθηκε ανεξάρτητα, από τον Τζον Γ.Φ. Φρανσίς και τον Βέρα Κουμπλανόφσκαγια in 1961.

Εφαρμογές

Ιδιοτιμές γεωμετρικών μετασχηματισμών

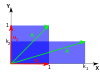
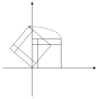
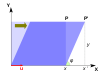
Ο ακόλουθος πίνακας παρουσιάζει κάποια παραδείγματα μετασχηματισμών μαζί με ένα πλάνο 2×2 πινάκων, ιδιοτιμών, και ιδιοδιανυσμάτων.

	κλιμάκωση	άνιση κλιμάκωση	περιστροφή	οριζόντια διάτμηση	Υπερβολική περιστροφή
απεικόνιση				Horizontal shear mapping
πίνακας	${\begin{bmatrix}k&0\\0&k\end{bmatrix}}$	${\begin{bmatrix}k_{1}&0\\0&k_{2}\end{bmatrix}}$	${\begin{bmatrix}c&-s\\s&c\end{bmatrix}}$ $c=\cos \theta$ $s=\sin \theta$	${\begin{bmatrix}1&k\\0&1\end{bmatrix}}$	${\begin{bmatrix}c&s\\s&c\end{bmatrix}}$ $c=\cosh \varphi$ $s=\sinh \varphi$
χαρακτηριστικό πολυώνυμο	$\ (\lambda -k)^{2}$	$(\lambda -k_{1})(\lambda -k_{2})$	$\lambda ^{2}-2c\lambda +1$	$\ (\lambda -1)^{2}$	$\lambda ^{2}-2c\lambda +1$
ιδιοτιμές $\lambda _{i}$	$\lambda _{1}=\lambda _{2}=k$	$\lambda _{1}=k_{1}$ $\lambda _{2}=k_{2}$	$\lambda _{1}=e^{\mathbf {i} \theta }=c+s\mathbf {i}$ $\lambda _{2}=e^{-\mathbf {i} \theta }=c-s\mathbf {i}$	$\lambda _{1}=\lambda _{2}=1$	$\lambda _{1}=e^{\varphi }$ $\lambda _{2}=e^{-\varphi }$,
αλγεβρική πολλαπλ. $\mu _{i}=\mu (\lambda _{i})$	$\mu _{1}=2$	$\mu _{1}=1$ $\mu _{2}=1$	$\mu _{1}=1$ $\mu _{2}=1$	$\mu _{1}=2$	$\mu _{1}=1$ $\mu _{2}=1$
γεωμετρική πολλαπ. $\gamma _{i}=\gamma (\lambda _{i})$	$\gamma _{1}=2$	$\gamma _{1}=1$ $\gamma _{2}=1$	$\gamma _{1}=1$ $\gamma _{2}=1$	$\gamma _{1}=1$	$\gamma _{1}=1$ $\gamma _{2}=1$
ιδιοδιανύσματα	Όλα τα μη-μηδενικά διανύσματα	$u_{1}={\begin{bmatrix}1\\0\end{bmatrix}}$ $u_{2}={\begin{bmatrix}0\\1\end{bmatrix}}$	$u_{1}={\begin{bmatrix}{\ }1\\-\mathbf {i} \end{bmatrix}}$ $u_{2}={\begin{bmatrix}{\ }1\\+\mathbf {i} \end{bmatrix}}$	$u_{1}={\begin{bmatrix}1\\0\end{bmatrix}}$	$u_{1}={\begin{bmatrix}{\ }1\\{\ }1\end{bmatrix}}$ $u_{2}={\begin{bmatrix}{\ }1\\-1\end{bmatrix}}.$

Η χαρακτηριστική εξίσωση για μία περιστροφή είναι μία Δευτεροβάθμια εξίσωση με διακρίνουσα $D=-4(\sin \theta )^{2}$, η οποία είναι αρνητικός αριθμός όταν το $\theta$ δεν είναι ακέραιο πολλαπλάσιο των 180°. Έτσι, εκτός από αυτές τις ειδικές περιπτώσεις, οι δύο ιδιοτιμές είναι μιγαδικοί αριθμοί, $\cos \theta \pm \mathbf {i} \sin \theta$; και όλα τα ιδιοδιανύσματα έχουν μη-πραγματικά στοιχεία. Πράγματι, πέρα απο αυτές τις ειδικές περιπτώσεις, κάθε τυχαία περιστροφή αλλάζει την κατεύθυνση κάθε μη-μηδενικού διανύσματος στο επίπεδο.

Εξισώσεις του Σρέντιγκερ

Οι κυματοσυναρτήσεις που σχετίζονται με τη δεσμευμένη κατάσταση ενός ηλεκτρονίου σε ένα άτομο υδρογόνου μπορούν να παρουσιαστούν ως Χαμιλτονιανές ατόμου υδρογόνου αλλά και ως τελεστές γωνιακής ορμής. Σχετίζονται με τα ιδιοδιανύσματα που μεταφράζονται ως οι ενέργειές τους (αυξάνοντας προς τα κάτω: $n=1,2,3,\ldots$) και με τις γωνιακές ορμές (αυξάνοντας κατά μήκος: s, p, d, ...). Η απεικόνιση δείχνει το τετράγωνο της απόλυτης τιμής της κυματοσυνάρτησης. Οι φωτεινότερες περιοχές αντιστοιχούν σε υψηλότερη πιθανότητα πυκνότητας πιθανότητα πυκνότητας για μια θέση μέτρησης. Το κέντρο κάθε φιγούρας είναι ο ατομικός πυρήνας, ένα πρωτόνιο.

Ένα παράδειγμα μιας εξίσωσης ιδιοτιμών όπου ο μετασχηματισμός $T$ αναπαρίσταται με όρους ενός διαφορικού τελεστή, είναι η ανεξάρτητη του χρόνου Εξίσωση Σρέντινγκερ στην κβαντική μηχανική:

$H\psi _{E}=E\psi _{E}\,$

όπου $H$, η χαμιλτονιανή, που είναι ένας δεύτερης-τάξης διαφορικός τελεστής και $\psi _{E}$, η κυματοσυνάρτηση, που είναι μια εκ των ιδιοσυναρτήσεων που αντιστοιχούν στην ιδιοτιμή $E$, δηλαδή η ενέργεια του.

Ωστόσο, στην περίπτωση που κάποιος ενδιαφέρεται μόνο στις λύσεις της δεσμευμένης κατάστασης τις εξίσωσης του Σρόντιγκερ, αναζητά την $\psi _{E}$ στον χώρο των τετραγωνικά ολοκληρώσιμων συναρτήσεων. Καθώς αυτός ο χώρος είναι Χώρος Χίλμπερτ με καλώς ορισμένο εσωτερικό γινόμενο, μπορεί να εισαχθεί ένα σύνολο βάσεων στο οποίο η $\psi _{E}$ και η $H$ μπορούν να μεταφραστούν ως μια μονοδιάστατη γραμμή ή έναν πίνακα αντίστοιχα. Αυτό επιτρέπει την αναπαράσταση της εξίσωσης Σρόντιγκερ σε μορφή πινάκων.

Η σημειογραφεία μπρά-κέτ χρησιμοποιείται συχνά σε αυτό το πλαίσιο. Ένα διάνυσμα, που αναπαριστά την κατάσταση ενός συστήματος, στον χώρο Χίλμπερτ των τετραγωνικά ολοκληρώσιμων συναρτήσεων αναπαρίσταται με $|\Psi _{E}\rangle$. Με αυτή τη σημειογραφεία, η εξίσωση του Σρόντιγκερ γράφεται:

$H|\Psi _{E}\rangle =E|\Psi _{E}\rangle$

όπου $|\Psi _{E}\rangle$ είναι μια ιδιοκατάσταση του $H$. Είναι ένας αυτοπροσδιοριζόμενος τελεστής, το απειροδιάστατο ανάλογο των Ερμιτιανών πινάκων (βλέπε Παρατηρήσιμοι). Ενώ στην περίπτωση των πινάκων, στην παραπάνω εξίσωση $H|\Psi _{E}\rangle$, γίνεται αντιληπτό πως είναι ένα διάνυσμα που λαμβάνεται με την εφαρμογή του μετασχηματισμού $H$ στην $|\Psi _{E}\rangle$.

Μοριακά τροχιακά

Στην κβαντική μηχανική, και συγκεκριμένα στην ατομική και μοριακή φυσική, μέσω της θεωρίας Χαρτρι-Φοκ, τα ατομικά και μοριακά τροχιακά μπορούν να οριστούν απο τα ιδιοδιανύσματα του χειριστή Φοκ. Οι αντίστοιχες ιδιοτιμές ερμηνεύονται ως τα δυναμικά ιονισμόυ από το θεώρημα του Κούπμαν. Στην περίπτωση αυτή, ο όρος ιδιοδιάνυσμα χρησιμοποιείται σε μια κάπως πιο γενική έννοια, αφού ο χειριστής Φοκ είναι άμεσα εξαρτώμενος στα τροχιακά και τις ιδιοτιμές τους. Αν κάποιος θέλει να υπογραμμίσει την οπτική αυτή, θα πρέπει να αναφέρεται σε ένα μη γραμμικό πρόβλημα ιδιοτιμών. Τέτοιες εξισώσεις λύνονται συνήθως από μια επαναληπτική διαδικασία, που στην περίπτωση αυτή ονομάζεται μέθοδος αυτο-συνεπή πεδίου. Στην κβαντική χημεία, η εξίσωση Χαρτρι-Φοκ συνήθως εφαρμόζεται σε ένα μη-ορθογώνιο σύστημα βάσεων. Αυτή η εφαρμογή είναι ένα γενικευμένο πρόβλημα ιδιοτιμών που ονομάζεται εξισώσεις Ρουθαν.

Γεωλογία και παγολογία

Στη γεωλογία, και συγκεκριμένα στη μελέτη της παραγωγής πάγου, τα ιδιοδιανύσματα και οι ιδιοτιμές χρησιμοποιούνται με τέτοιο τρόπο. ώστε ένας όγκος πληροφοριών σχετικός με τον προσανατολισμό και το βάθος γεωλογικών κλαστικών συστατικών, μπορεί να περιγραφεί σε έναν τρισδιάστατο χώρο, με έξι νούμερα. Στο πεδίο, ο γεωλόγος μπορεί να συλλέξει τέτοιου είδους δεδομένα για εκατοντάδες χιλιάδες κλαστικά με ένα δείγμα χώματος, που μπορεί να συγκριθεί μόνο γραφικά, για παράδειγμα με ένα τριγωνικό διάγραμμα, ή σαν ένα στερεοδίκτυο σε ένα δίκτυο Γουλφ.

Το αποτέλεσμα αυτού του αισθητήρα προσανατολισμού, βρίσκεται στους τρεις ορθογώνιους )καθετους) άξονες του χώρου. Τα τρία ιδιοδιανύσματα ορίζονται ως $v_{1},v_{2},v_{3}$ από τις ιδιοτιμές τους $E_{1}\geq E_{2}\geq E_{3}$; Το $v_{1}$ λοιπόν είναι τα πρωτεύοντα στοιχεία προσανατολισμού και βάθους του κλαστικού, το $v_{2}$ είναι τα δευτερεύοντα και το $v_{3}$ είναι τα τριτεύοντα, αναλογικά με τη δύναμη. Ο προσανατολισμός του κλαστικού ορίζεται ως η κατεύθυνση του ιδιοδιανύσματος, πάνω σε ένα ανεμολόγιο των 360°. Το βάθος μετράται ως η ιδιοτιμή, το μόντουλο του αισθητήρα: αυτό ορίζεται από 0° (καθόλου βάθος) έως 90° (κάθετα). Οι αντίστοιχες τιμές των $E_{1}$, $E_{2}$, και $E_{3}$ υπαγορεύονται από τη φύση του ιζήματος του υλικού. Αν $E_{1}=E_{2}=E_{3}$, το υλικό ονομάζεται ισοτροπικό. Αν $E_{1}=E_{2}>E_{3}$, το υλικό ονομάζεται επίπεδο. Αν $E_{1}>E_{2}>E_{3}$, το υλικό ονομάζεται γραμμικό.

Ανάλυση κυρίων συνιστωσών

ΑΚΣ της πολυμεταβλητής κατανομής Γκάους κέντρου $(1,3)$ με τυπική απόκλιση 3 στη κατευθυνση $(0.878,0.478)$ και  1 στην ορθογώνια διεύθυνση. Τα διανύσματα που φαίνονται είναι ιδιοδιανύσματα μονάδας του (συμμετρικού, θετικά-ημιορισμένου) πίνακα συνδιασποράς κλιμακωτά ως προς την τετραγωνική ρίζα τις αντίστοιχης ιδιοτιμής. (Όπως και στη μονοδιάστατη περίπτωση, η τετραγωνική ρίζα λαμβάνεται καθώς η τυπική απόκλιση είναι πιο εύκολα οπτικοποιήσιμη από τη διακύμανση.

Η ιδιοσύνθεση ενός συμμετρικού θετικά ημιορισμένου πίνακα αποδίδει μία ορθογώνια βάση ιδιοδιανυσμάτων, καθένα εκ τον οποίων έχει μια μη-αρνητική ιδιοτιμή. Η ορθογώνια αποσύνθεση ενός (ΑΚΣ) πίνακα χρησιμοποιείται στην ανάλυση πολλών μεταβλητών, όπου το δείγμα με πίνακα συνδιασποράς είναι (ΑΚΣ). Αυτή η ορθογώνια αποσύνθεση καλείται ανάλυση κυρίων συνιστωσών (ΑΚΣ) στη στατιστική. Η ΑΚΣ μελετά γραμμικούς συσχετισμούς μεταξύ μεταβλητών. η ΑΚΣ εφαρμόζεται σε πίνακες συνδιασποράς ή σε πίνακες συσχετισμού (στους οποίους κάθε μεταβλητή είναι κλιμακωτή έτσι ώστε η διασπορά του δείγματος να ισούται με ένα). Για τους πίνακες συνδιασποράς και συσχετισμού, τα ιδιοδιανύσματα αντιστοιχούν στις κύριες συνιστώσες και οι ιδιοτιμές στις εξηγημένες διασπορές των κυρίων συνιστωσών. Η ανάλυση κυρίων συνιστωσών του πίνακα συσχετισμού παρέχει μία ορθογώνια ιδιοβάση για τον χώρο των παρατηρούμενων δεδομένων: Σε αυτή την βάση, οι μεγαλύτερες ιδιοτιμές αντιστοιχούν στις κύριες-συνιστώσες που σχετίζονται περισσότερο με την συμμεταβλητότητα ανάμεσα σε έναν αριθμό παρατηρούμενων δεδομένων.

Η ανάλυση κυρίων συνιστωσών χρησιμοποιείται για την μελέτη μεγάλων συνόλων δεδομένων, όπως αυτά που βλέπουμε στην εξόρυξη δεδομένων, χημική έρευνα, ψυχολογία, και στο μάρκετινγκ. Η ΑΚΣ είναι δημοφιλής κυρίως στην ψυχολογία, στον τομέα της ψυχομετρικής. Στην Q μεθοδολογία, οι ιδιοτιμές του πίνακα συσχετισμού καθορίζουν την κρίση του Q-μεθοδολόγου στην πρακτική σημαντικότητα (που διαφέρει από την στατιστική σημαντικότητα του ελέγχου της υπόθεσης): Οι παράγοντες με ιδιοτιμές μεγαλύτερες του 1 θεωρούνται πρακτικά σημαντικές, το οποίο οδηγεί στην εξήγηση σημαντικού ποσού των δεδομένων μεταβλητότητας, ενώ οι ιδιοτιμές που είναι μικρότερες του 1.00 θεωρούνται πρακτικά ασήμαντες, εξηγώντας μόνο ένα αμελητέο ποσοστό των δεδομένων μεταβλητότητας. Γενικότερα, η ανάλυση κυριών συνιστωσών μπορεί να χρησιμοποιηθεί ως μέθοδος ανάλυσης παραγόντων σε μοντέλα διαρθρωτικής εξίσωσης.

Ανάλυση δόνησης

1η πλάγια καμπή (βλέπε δόνηση για περισσότερους τύπους δονήσεως)

Προβλήματα ιδιοτιμών παρουσιάζονται φυσικά στην ανάλυση δονήσεων των μηχανικών δομών με πολλούς βαθμούς ελευθερίας. Οι ιδιοτιμές χρησιμοποιούνται για τον προσδιορισμό των φυσικών συχνοτήτων (ή ιδιοσυχνοτήτων) της δόνησης, και τα ιδιοδιανύσματα για τον προσδιορισμό των μορφών των τρόπων δόνησης. Συγκεκριμένα, δόνηση χωρίς απόσβεση κραδασμών διέπεται από

$m{\ddot {x}}+kx=0$

ή

$m{\ddot {x}}=-kx$

που είναι, η επιτάχυνση αναλογικά με την θέση (π.χ., περιμένουμε το $x$ να είναι ημιτονοειδές ως προς τον χρόνο). Σε $n$ διαστάσεις, $m$ γίνεται ένας πίνακας μάζας και $k$ ένας πίνακας ακαμψίας. Αποδεκτές λύσεις είναι λοιπόν ένας γραμμικός συνδυασμός λύσεων του γενικευμένου προβλήματος ιδιοτιμών

$-kx=\omega ^{2}mx$

όπου $\omega ^{2}$ είναι η ιδιοτιμή και $\omega$ είναι η γωνιακή συχνότητα. Οι τρόποι κύριας δόνησης διαφέρουν από τις κύριες λειτουργίες συμμόρφωσης, που είναι ιδιοδιανύσματα του $k$ και μόνο αυτού. Επιπλέον, η δόνηση με απόσβεση κραδασμών, διέπεται από

$m{\ddot {x}}+c{\dot {x}}+kx=0$

και οδηγεί σε αυτό που καλείται τετραγωνικό πρόβλημα ιδιοτιμών,

$(\omega ^{2}m+\omega c+k)x=0.$

Αυτό μπορεί αν αναχθεί σε ένα γενικευμένο πρόβλημα ιδιοτιμών μέσω έξυπνης άλγεβρας με την ανάγκη, όμως, επίλυσης μεγάλων συστημάτων.

Οι ορθολογικές ιδιότητες ιδιοδιανυσμάτων επιτρέπουν την αποσύνδεση των διαφορικών εξισώσεων έτσι ώστε το σύστημα να αναπαρασταθεί ως γραμμικό άθροισμα των ιδιοδιανυσμάτων. Το πρόβλημα των ιδιοτιμών μιγαδικών δομών συνήθως λύνεται χρησιμοποιώντας μέθοδο πεπερασμένων στοιχείων, αλλά έξυπνα γενικεύει την λύση σε μια κλιμακωτής-τιμής στα προβλήματα δόνησης.

Ιδιοπρόσωπα

Ιδιοπρόσωπα σαν παραδείγματα ιδιοδιανυσμάτων

Στην επεξεργασία εικόνας, οι επεξεργασμένες εικόνες προσώπων μπορούν να εκφραστούν σαν διανύσματα, τα στοιχεία των οποίων είναι οι φωτεινότητες για κάθε πίξελ. Η διάσταση του διανυσματικού αυτού χώρου είναι ο αριθμός των πιξελ. Τα ιδιοδιανύσματα του πίνακα συνδιακύμανσης συνδέονται με ένα μεγάλο σύνολο απο κανονικοποιημένες εικόνες προσώπων, που ονομάζονται ιδιοπρόσωπα. Αυτό είναι ένα παράδειγμα ανάλυσης κυρίων συνιστωσών. Τα ιδιοπρόσωπα είναι πολύ χρήσιμα για να εκφράζουν κάθε εικόνα προσώπων σαν ένα γραμμικό συνδυασμό μερικών από αυτά. Στην αναγνώριση προσώπων, παρακλάδι της Βιομετρίας, τα ιδιοπρόσωπα παρέχουν ένα μέσο για να εφαρμοστεί συμπίεση δεδομένων σε πρόσωπα για σκοπούς ταυτοποίησης. Έρευνες σχετικές με τα ιδιο-οπτικά συστήματα που προσδιορίζουν χειρονομίες, γίνονται επίσης.

Παρόμοια με αυτές τις έννοιες, οι ιδιοφωνές αντιπροσωπεύουν τη γενική κατεύθυνση της μεταβλητότητας σε ανθρώπινες προφορές μιας ιδιαίτερης έκφρασης, όπως μια λέξη σε μία γλώσσα. Βασιζόμενη σε ένα γραμμικό συνδυασμό τέτοιων ιδιοφωνών, μπορεί να κατασκευαστεί μια νέα φωνητική προφορά της λέξης αυτής. Οι έννοιες αυτές έχουν φανεί χρήσιμες σε συστήματα αυτόματης αναγνώρισης λόγου, για ηχητική προσαρμογή.

Τανυστής στιγμιαίας αδράνειας

Στη μηχανική, τα ιδιοδιανύσματα του τανυστή αδράνειας καθορίζουν τους κύριους άξονες ενός στερεού σώματος. Ο τανυστής στιγμιαίας αδράνειας είναι μια ποσότητα κλειδί, που είναι απαραίτητη για να προσδιορίστει η περιστροφή ενός στερεού σώματος γύρω από το κέντρο μάζας του.

Τανυστής πίεσης

Στη στερεά μηχανική, ο τανυστής πίεσης είναι συμμετρικός και επομένως μπορεί να αποσυντεθεί σε ένα διαγώνιο τανυστή με ιδιοτιμές στη διαγώνιο και ιδιοδιανύσματα σαν βάση. Επειδή είναι διαγώνιος, σ'αυτή τη δομη, ο τανυστής πίεσης δεν έχει διάτμητα στοιχεία. Τα στοιχεία που έχει είναι τα πρωταρχικά στοιχεία.

Ιδιοτιμές ενός γραφήματος

Στην φασματική γραφική θεωρία, μια ιδιοτιμή ενός γραφήματος ορίζεται ως μια ιδιοτιμή του αντίστοιχου πίνακα γειτνίασης $A$ του γραφήματος, ή (περισσότερο) του λαπλασιανού πίνακα του γραφήματος (βλέπε επίσης Διακριτός χειριστής Λαπλάς), που είναι ή $T-A$ (μερικές φορές με ονομασία συνδυαστικός Λαπλασιανός) είτε $I-T^{-1/2}AT^{-1/2}$ (μερικές φορές με ονομασία κανονικοποιημένος Λαπλασιανός), όπου ο $T$ είναι ένας διαγώνιος πίνακας με $T_{ii}$ ισό με το βαθμότης κορυφής $v_{i}$, και στον $T^{-1/2}$, το $i$-στο διαγώνιο στοιχείο είναι η ${\sqrt {\operatorname {deg} (v_{i})}}$. Το $k$-στο πρωταρχικό ιδιοδιάνυσμα ενός γραφήματος, προσδιορίζεται ως το ιδιοδιάνυσμα που αντιστοιχεί ή στην $k$-στη μεγαλύτερη, είτε στην $k$-στη μικρότερη ιδιοτιμή του Λαπλασιανού. Το πρώτο πρωταρχικό ιδιοδιάνυσμα του γραφήματος, είναι επίσης γνωστό ως το πρωταρχικό ιδιοδιάνυσμα.

Το πρωταρχικό ιδιοδιάνυσμα χρησιμοποιείται για τη μέτρηση της εγκεντρότητας των κορυφών του. Ενα παράδειγμμα, είναι ο αλγόριθμος PageRank της Google. Το πρωταρχικό ιδιοδιάνυσμα του επεξεργασμένου αντίστοιχου πίνακα γειτνίασης του γραφήματος του παγκοσμίου δικτύου, έχει τις σελιδοβαθμίδες ως στοιχεία του. Το διάνυσμα αυτό αντιστοιχεί στη στάσιμη κατανομή της Αλυσίδας Μαρκόφ που αντιπροσωπεύεται από τον γραμμο-κανονικοποιημένο αντίστοιχο πίνακα. Παρολαυτά, ο αντίστοιχος πίνακας πρέπει πρώτα να τροποποιηθεί για να σιγουρευτεί ότι μια στάσιμη κατανομή υπάρχει. Το δεύτερο μικρότερο ιδιοδιάνυσμα μπορει να χρησιμοποιηθεί για να χωρίσει το γράφημα σε συμπλέγματα, μέσω της φασματικής συμπλεγματοποίησης. Άλλες μέθοδοι είναι επίσης διαθέσιμές για συμπλεγματοποίηση.

Βασικός ρυθμός αναπαραγωγής

Ο βασικός ρυθμός αναπαραγωγής ($R_{0}$) είναι ένας θεμελιώδης αριθμος για τη μελέτη του τρόπου εξάπλωσης των λοιμώξεων. Αν ένα μολυσμένο άτομο τοποθετηθεί σε έναν πληθυσμό με εντελώς ευαίσθητα άτομα, τότε ο $R_{0}$ είναι ο μέσος αριθμός ατόμων που θα μολύνει ένα μολυσμένο άτομο. Ο χρόνος παραγωγής μιας λοίμωξης, είναι το χρονικό διάστημα $t_{G}$ που μεσολαβεί ανάμεσα στα γεγονότα, το ένα άτομο να μολυνθεί, μέχρι το επόμενο άτομο να μολυνθεί. Σε έναν ετερογενή πληθυσμό, ο πίνακας της επόμενης γενιάς καθορίζει πόσα άτομα του πληθυσμού θα μολυνθούν, όταν έχει περάσει χρόνος $t_{G}$. Η $R_{0}$ είναι λοιπόν η μεγαλύτερη ιδιοτιμή του πίνακα της επόμενης γενιάς.

Εξωτερικοί Σύνδεσμοι

1. Εφαρμογή για τον υπολογισμό των πραγματικών ιδιοτιμών και ιδιοδιανυσμάτων ενός πίνακα (EigenCalc).