Μετασχηματισμός Φουριέ
| Το λήμμα δεν περιέχει πηγές ή αυτές που περιέχει δεν επαρκούν. |
Ο μετασχηματισμός Fourier, το όνομά του οποίου προήλθε από τον Ζοζέφ Φουριέ, είναι ένας μαθηματικός μετασχηματισμός με πολλές εφαρμογές στη φυσική και την μηχανική. Πολύ συχνά μετατρέπει μια μαθηματική συνάρτηση του χρόνου, f(t), σε μια νέα συνάρτηση,που μερικές φορές συμβολίζεται με ή F, των οποίων η μονάδα μέτρησής τους είναι η συχνότητα με την οποία εμφανίζουν μονάδες κύκλου / δευτερόλεπτο ( Hertz ) ή ακτίνια ανά δευτερόλεπτο. Η νέα συνάρτηση είναι τότε γνωστή ως μετασχηματισμός Fourier ή και ως φάσμα συχνοτήτων της συνάρτησης f. Ο μετασχηματισμός Fourier είναι επίσης μια αντιστρέψιμη συνάρτηση. Έτσι, με δεδομένη την συνάρτηση μπορεί να προσδιοριστεί η αρχική συνάρτηση, f. Οι f και είναι, επίσης, αντίστοιχα, γνωστές ως πεδίο του χρόνου και της συχνότητας, αναπαραστάσεις του ίδιου «γεγονότος».Τις περισσότερες φορές ίσως, η f είναι μια πραγματική συνάρτηση, και η είναι μια μιγαδική συνάρτηση, όπου ένας μιγαδικός αριθμός περιγράφει τόσο το πλάτος όσο και τη φάση της αντίστοιχης συνιστώσας συχνότητας. Σε γενικές γραμμές, η f είναι επίσης σύνθετη, όπως η αναλυτική αναπαράσταση μιας πραγματικής συνάρτησης. Ο όρος "μετασχηματισμός Fourier" αναφέρεται τόσο στην συνάρτηση μετασχηματισμού όσο και στην μιγαδική συνάρτηση που παράγει.
Στην περίπτωση μιας περιοδικής συνάρτησης (για παράδειγμα, μια συνεχής, αλλά όχι απαραίτητα ημιτονοειδούς μουσικού ήχου), ο μετασχηματισμός Fourier μπορεί να απλοποιηθεί με τον υπολογισμό ενός διακριτού σύνολο σύνθετου πλάτους, που ονομάζεται συντελεστής σειράς Fourier. Επίσης, όταν μια συνάρτηση του πεδίου χρόνου λειτουργίας χρησιμοποιηθεί για τη διευκόλυνση της αποθήκευσης ή της επεξεργασίας του υπολογιστή , είναι ακόμα δυνατό να αναδημιουργήσει μια έκδοση του αρχικού μετασχηματισμού Fourier σύμφωνα με τον τύπο άθροισης Poisson, που επίσης είναι γνωστή ως μετασχηματισμός διακριτού χρόνου Fourier . Τα θέματα αυτά εξετάζονται σε χωριστά άρθρα. Για μια επισκόπηση αυτών και άλλες συναφείς δραστηριότητες, ανατρέξτε στην ανάλυση Fourier ή στην Λίστα που σχετίζεται με τους μετασχηματισμούς Fourier.
Ορισμός[Επεξεργασία | επεξεργασία κώδικα]
Υπάρχουν πολλές κοινές συμβάσεις για τον καθορισμό του μετασχηματισμού Fourier ƒ μιας ολοκληρώσιμης συνάρτησης f : R → C (Kaiser 1994, σ. 29), (Rahman 2011, σ. 11). Αυτό το άρθρο θα χρησιμοποιήσει τον ορισμό:
- , για κάθε πραγματικό αριθμό ξ.
Όταν η ανεξάρτητη μεταβλητή x αντιπροσωπεύει τον χρόνο (με το SI μονάδα δευτερολέπτου), ο μετασχηματισμός της μεταβλητής ξ αντιπροσωπεύει τη συχνότητα (σε Hertz). Υπό κατάλληλες συνθήκες, η f(x) προσδιορίζεται από την ƒ μέσω του αντίστροφου μετασχηματισμού:
- για κάθε πραγματικό αριθμό x.
Η δήλωση ότι η f(x) μπορεί να ανακατασκευαστεί από ƒ είναι γνωστή ως το θεώρημα αντιστροφής Fourier και εισήχθη για πρώτη φορά στη Φουριέ Αναλυτική θεωρία της θερμότητας (Fourier 1822, p. 525), (Fourier & Freeman 1878, σ. 408). Παρόλο που θα μπορούσε να θεωρηθεί ως απόδειξη από τα σύγχρονα πρότυπα, αυτή δόθηκε πολύ αργότερα (Titchmarsh 1948, σ. 1). Οι λειτουργίες f και ƒ(x) συχνά αναφέρονται ως ένα αναπόσπαστο ζεύγος Fourier ή ζεύγος μετασχηματισμού Fourier (Rahman 2011, σ. 10).
Για άλλες κοινές συμβάσεις και συμβολισμούς, συμπεριλαμβανομένης της χρήσης της γωνιακής συχνότητας ω, αντί της συχνότητας ξ, δείτε Άλλες συμβάσεις και άλλοι συμβολισμοί παρακάτω. Ο μετασχηματισμός Fourier σε Ευκλείδειους χώρους αντιμετωπίζεται χωριστά, όπου η μεταβλητή x αντιπροσωπεύει συχνά τη θέση και η ξ την ορμή.
Εισαγωγή[Επεξεργασία | επεξεργασία κώδικα]

Το κίνητρο για το μετασχηματισμό Fourier προέρχεται από τη μελέτη της σειράς Fourier .Στη μελέτη των σειρών Fourier, οι περίπλοκες, αλλά περιοδικές συναρτήσεις έχουν γραφτεί ως το άθροισμα των απλών κυμάτων που στα μαθηματικά αντιπροσωπεύεται από ημίτονα και συνημίτονα . Ο μετασχηματισμός Fourier είναι μια επέκταση της σειράς Fourier που προκύπτει όταν η περίοδος της συνάρτησης που εκπροσωπεί επιμηκύνεται και αφήνεται να προσεγγίσει το άπειρο. ( Taneja 2008 , σελ.. 192)Λόγω των ιδιοτήτων του ημιτόνου και συνημίτονου, είναι δυνατόν να ανακτήσει το πλάτος του κάθε κύμα σε μια σειρά Fourier χρησιμοποιώντας ολοκλήρωμα. Σε πολλές περιπτώσεις, είναι επιθυμητό να χρησιμοποιούν τον τύπο του Όιλερ, ο οποίος αναφέρει ότι ηe2πiθ= cos(2πθ) + isin(2πθ), μπορεί να γραφεί σε σειρά Fourier όσον αφορά τα βασικά κύματα e2πiθ . Αυτό έχει το πλεονέκτημα της απλοποίησης πολλών από τους εμπλεκόμενους τύπους, και παρέχει ένα σκεύασμα για τη σειρά Fourier που περισσότερο μοιάζει με τον ορισμό που ακολουθείται σε αυτό το άρθρο. Για να είναι συντελεστές Fourier μιγαδικής μεταβλητής καθίσταται αναγκαίο η γραφή των ημίτονων και συνημίτονων ως εκθετικών συναρτήσεων. Η συνήθης ερμηνεία αυτού του μιγαδικού αριθμού είναι ότι δίνει τόσο το πλάτος (ή το μέγεθος) του παρόντος κύματος στη λειτουργία και τη φάση (ή την αρχική γωνία) του κύματος. Αυτές οι μιγαδικές εκθετικές συναρτήσεις μερικές φορές περιέχουν αρνητικές "συχνότητες". Αν θ μετριέται σε δευτερόλεπτα τα κύματα e2πiθ και e−2πiθ ολοκληρώνουν έναν κύκλο σε ένα δευτερόλεπτο, αλλά αντιπροσωπεύουν διαφορετικές συχνότητες στον μετασχηματισμού Fourier. Ως εκ τούτου, η συχνότητα πλέον δεν μετρά τον αριθμό των κύκλων ανά μονάδα χρόνου, αλλά εξακολουθεί να είναι στενά συνδεδεμένα.
Υπάρχει μια στενή σχέση μεταξύ του ορισμού των σειρών Fourier και του μετασχηματισμού Fourier για τις συναρτήσεις f που είναι μηδέν έξω από ένα χρονικό διάστημα. Για μια τέτοια συνάρτηση, μπορούμε να υπολογίσουμε την σειρά Fourier για οποιοδήποτε χρονικό διάστημα που περιλαμβάνει τα σημεία όπου f δεν είναι πανομοιότυπα μηδέν. Ο μετασχηματισμός Fourier ορίζεται επίσης για μια τέτοια λειτουργία. Όπως έχουμε αυξήσει το μήκος του διαστήματος στο οποίο υπολογίζουμε τη σειρά Fourier, τότε οι συντελεστές της σειράς Fourier αρχίζουν να μοιάζουν με το μετασχηματισμό Fourier και το άθροισμα της σειράς Fourier της f αρχίζει να μοιάζει με τον αντίστροφο μετασχηματισμό Fourier. Για να το εξηγήσουμε αυτό ακριβέστερα, ας υποθέσουμε ότι το Τ είναι αρκετά μεγάλο, έτσι ώστε το διάστημα [−T/2,T/2],να περιέχει το διάστημα στο οποίο f δεν είναι πανομοιότυπα μηδέν. Στη συνέχεια, η κ -οστή σειράς συντελεστής γnδίνεται από:
Συγκρίνοντας αυτό τον ορισμό με τον μετασχηματισμό Fourier, προκύπτει ότι cn = ƒ(n/T)από το f ( x ) είναι μηδέν εκτός[−T/2,T/2].Έτσι, οι συντελεστές Fourier είναι μόνο οι τιμές του μετασχηματισμού Fourier σε ένα δειγματικό πλέγμα πλάτους 1/T. Όπου T αυξάνει τους συντελεστές Fourier αντιπροσωπεύοντας καλύτερα το μετασχηματισμό Fourier της συνάρτησης.
Υπό κατάλληλες συνθήκες, το άθροισμα της σειράς Fourier της f θα είναι ίσο με τη συνάρτηση f . Με άλλα λόγια, f μπορεί να γραφτεί:
όπου το τελευταίο άθροισμα είναι απλά το πρώτο που έχει ξαναγραφεί με τη χρήση των ορισμών ξn = n/T, and Δξ = (n + 1)/T − n/T = 1/T. Αυτό το δεύτερο άθροισμα είναι ένα άθροισμα Riemann , και έτσι αφήνοντας το T → ∞ θα συγκλίνει προς το ολοκλήρωμα του αντίστροφου μετασχηματισμού Fourier που δίνεται στο τμήμα του ορισμού. Υπό κατάλληλες συνθήκες το επιχείρημα αυτό μπορεί να γίνει ακριβής ( Stein & Shakarchi 2003 ).
Στη μελέτη των σειρών Fourier οι αριθμοί cn θα μπορούσε να θεωρηθεί ως η «ποσότητα» του κύματος που παρουσιάζεται στη σειρά Fourier ως f . Ομοίως, όπως φαίνεται ανωτέρω, ο μετασχηματισμός Fourier μπορεί να θεωρηθεί ως μια συνάρτηση που μετρά τον αριθμό από κάθε επιμέρους συχνότητα που παρουσιάζεται στην συνάρτηση μας fκαι μπορεί να ανασυνδυάσει αυτά τα κύματα χρησιμοποιώντας ολοκλήρωμα (ή "συνεχής άθροισμα") για να αναπαράγει την αρχική συνάρτηση.
Παράδειγμα[Επεξεργασία | επεξεργασία κώδικα]
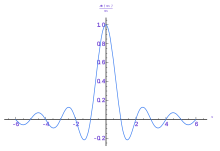
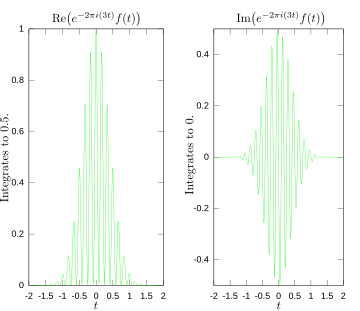
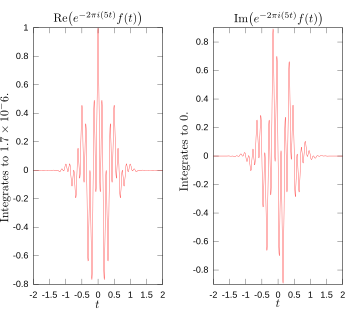
Οι παρακάτω εικόνες παρέχουν μια οπτική απεικόνιση του πώς ο μετασχηματισμός Fourier μετρά αν μια συχνότητα είναι παρούσα σε μια συγκεκριμένη συνάρτηση. Η συνάρτηση απεικονίζει τηνf(t) = cos(6πt) e-πt2 να ταλαντώνεται σε 3 hertz (εάν t μέτρα δευτερόλεπτα) και τείνει γρήγορα στο μηδέν. (Ο δεύτερος παράγοντας στην εξίσωση αυτή είναι μια συνάρτηση φάκελος που διαμορφώνει τη συνεχή ημιτονοειδή συνάρτηση σε ένα σύντομο παλμό. Η γενική μορφή της είναι μια συνάρτηση Gauss ). Αυτή η λειτουργία ήταν ειδικά επιλεγμένα για να έχουν μια πραγματική μετασχηματισμού Fourier η οποία μπορεί εύκολα να καταγράφεται. Η πρώτη εικόνα περιέχει γράφημα της. Αυτή η συνάρτηση ήταν ειδικά επιλεγμένη για να έχουμε ένα πραγματικό μετασχηματισμό Fourier ο οποίος μπορεί εύκολα να καταγράφει. Η πρώτη εικόνα περιέχει το γράφημα της. Για να υπολογιστεί f (3) θα πρέπει να ενσωματώσουμε την e−2πi(3t)f(t). Η δεύτερη εικόνα δείχνει το πεδίο από τα πραγματικά και φανταστικά μέρη αυτής της συνάρτησης. Το πραγματικό μέρος του ολοκληρωτέου είναι σχεδόν πάντα θετικό, γιατί όταν f ( t ) είναι αρνητική,το πραγματικό μέρος της e−2πi(3t)είναι αρνητικό.Καθώς και επειδή ταλαντώνονται με τον ίδιο ρυθμό, όταν η f ( t ) είναι θετική, έτσι το πραγματικό μέρος της e−2πi(3t),το αποτέλεσμα είναι ότι όταν θα ενσωματώσει το πραγματικό μέρος της ολοκληρωτέου μπορεί να πάρουμε ένα σχετικά μεγάλο αριθμό (σε αυτή την περίπτωση 0.5).Από την άλλη πλευρά, όταν προσπαθούμε να μετρήσουμε μια συχνότητα που δεν είναι παρόν, όπως στην περίπτωση της f (5), το ολοκλήρωμα ταλαντώνεται αρκετά, έτσι ώστε το ολοκλήρωμα να είναι πολύ μικρό. Η γενική κατάσταση μπορεί να είναι λίγο πιο περίπλοκη από αυτό, αλλά το πνεύμα είναι το πώς ο μετασχηματισμός Fourier μετρά πόσο μια μεμονωμένη συχνότητα είναι παρούσα σε μια συνάρτηση f ( t ).
-
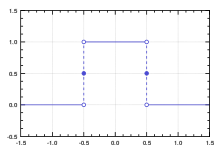
Αρχική λειτουργία δείχνει ταλάντωση 3 3 hertz.
-
Πραγματικά και φανταστικά μέρη της integrand για μετασχηματισμού Fourier σε 3 hertz.
-
Πραγματικά και φανταστικά μέρη της integrand για μετασχηματισμού Fourier σε 5 hertz .
-
Fourier Μετασχηματισμού Fourier με 3 και 5 hertz επισήμανση.
Ιδιότητες του μετασχηματισμού Fourier[Επεξεργασία | επεξεργασία κώδικα]
Εδώ υποθέτουμε ότι f(x), g(x) και h(x) είναι ολοκληρώσιμες συναρτήσεις , είναι Lebesgue μετρήσιμες στην πραγματική ευθεία, και πληρούν:
Ορίζουμε το μετασχηματισμό Fourier των συναρτήσεων αυτών ως , και αντίστοιχα.
Βασικές ιδιότητες[Επεξεργασία | επεξεργασία κώδικα]
Ο μετασχηματισμός Fourier έχει τις εξής βασικές ιδιότητες: ( Pinsky 2002 ).
- Γραμμικότητα
- Για οποιεσδήποτε μιγαδικοί αριθμοί a και b,αν h(x) = af(x) + bg(x), τότε
- Μετατόπιση
- Για κάθε πραγματικό αριθμό x0,αν τότε
- Διαμόρφωση
- Για κάθε πραγματικό αριθμό ξ0 αν τότε
- Κλιμάκωση
- Για ένα μη μηδενικό πραγματικό αριθμό a, αν h(x) = f(ax), τότε Η περίπτωση a = −1 οδηγεί στο χρόνο αναστροφής ο οποίος αναφέρει: αν h(x) = f(−x), τότε
- Σύζευξη
- Αν τότε
- Ειδικότερα, εάν f είναι πραγματική, τότε έχουμε
- Και αν fείναι καθαρά φανταστική,έχουμε
Αντιστρεψιμότητα και η περιοδικότητα[Επεξεργασία | επεξεργασία κώδικα]
Υπό τις κατάλληλες συνθήκες η συνάρτηση f, μπορεί να ανακτηθεί από τον μετασχηματισμό Φουριέρ Πράγματι, δηλώνοντας το μετασχηματισμό Fourier τέτοιο ώστε τότε με τις κατάλληλες συναρτήσεις, εφαρμόζοντας τον μετασχηματισμό Fourier δύο φορές και αντιστρέφοντας απλά την συνάρτηση : μπορούμε να πάρουμε την ανάστροφη.Δεδομένου ότι η αναστροφή του χρόνου είναι δύο φορές περιοδική,εφαρμόζουμε δύο φορές τις συναρτήσεις ώστε ο μετασχηματισμός Fourier να είναι τέσσερις φορές περιοδική,και ομοίως ο αντίστροφος μετασχηματισμός Fourier που μπορεί να προκύψει από την εφαρμογή του μετασχηματισμού Fourier τρεις φορές: : Ειδικότερα, ο μετασχηματισμός Fourier είναι αντιστρέψιμος (υπό κατάλληλες συνθήκες ).
Πιο συγκεκριμένα,καθορίζοντας ως , που αντιστρέφει το χρόνο, με :
Οι ισότητες αυτές απαιτούν προσεκτικό καθορισμό του διαστήματος των εν λόγω συναρτήσεων, τον ορισμό της ισότητας των συναρτήσεων (ισότητα σε κάθε σημείο συνεπάγεται ισότητα σχεδόν παντού ) και τον ορισμό της ισότητας των φορέων που, καθορίζει την τοπολογία στο πεδίο ορισμού της συνάρτησης και στο πεδίο του φορέα. Αυτά δεν επαληθεύονται για όλες τις συναρτήσεις, αλλά επαληθεύονται κάτω από διάφορες συνθήκες, οι οποίες αποτελούν το περιεχόμενο των διαφόρων μορφών του θεωρήματος αναστροφής Fourier .
Αυτή η τετραπλή περιοδικότητα του μετασχηματισμού Fourier είναι παρόμοια με μια περιστροφή του επιπέδου κατά 90 °,καθώς δύο φορές επανάληψη δίδει μία αντιστροφή, και στην πραγματικότητα αυτή η αναλογία μπορεί να γίνει ακριβής.Ενώ ο μετασχηματισμός Fourier μπορεί απλά να ερμηνευθεί ως μεταγωγός από το πεδίο του χρόνου στο πεδίο συχνοτήτων,με τον αντίστροφο μετασχηματισμό Fourier συμβαίνει το αντίστροφο από το πεδίο συχνοτήτων στο πεδίο του χρόνου, πιο γεωμετρικά αυτό μπορεί να ερμηνευθεί ως μία περιστροφή κατά 90 ° στο πεδίο χρόνου-συχνότητας θεωρώντας ως χρόνο τον άξονα των Χ και ως συχνότητα τον άξονα των Υ και ο μετασχηματισμός Fourier μπορεί να γενικευθεί με το κλασματικό μετασχηματισμό Fourier , ο οποίος περιλαμβάνει περιστροφές από άλλες γωνίες.Αυτά μπορεί περαιτέρω να γενικευτούν σε κανονικούς γραμμικούς μετασχηματισμούς ,οι οποίοι μπορεί να απεικονιστούν πάνω στην ειδική γραμμική ομάδα SL 2 ( R ) στο επίπεδο χρόνου-συχνότητας, με το διατήρηση συμπλεκτικών μορφών που αντιστοιχούν στην αρχή της αβεβαιότητας . Αυτή η προσέγγιση έχει ιδιαίτερα μελετηθεί στην επεξεργασία σήματος , σύμφωνα με την ανάλυση χρόνου-συχνότητας .
Ομοιόμορφη συνέχεια και λήμμα Riemann-Lebesgue[Επεξεργασία | επεξεργασία κώδικα]
Ο μετασχηματισμός Fourier μπορεί να καθοριστεί σε ορισμένες περιπτώσεις για μη ολοκληρώσιμες συναρτήσεις , αλλά ο μετασχηματισμός Fourier για τις ολοκληρώσιμες συναρτήσεις έχει αρκετά ισχυρές ιδιότητες. Ο μετασχηματισμός Fourier, ƒ, κάθε ολοκληρώσιμη συνάρτηση f είναι ομοιόμορφα συνεχής και (Katznelson 1976) Με την Riemann-Lebesgue λήμμα ( Stein & Weiss 1971 ),
Ωστόσο, ƒ δεν χρειάζεται να είναι ολοκληρώσιμη. Για παράδειγμα, ο μετασχηματισμός Fourier της ορθογώνιου συνάρτησης , η οποία είναι ολοκληρώσιμη, είναι η sinc συνάρτηση, η οποία δεν είναι Lebesgue ολοκληρώσιμη , επειδή τα ολοκληρώματα συμπεριφέρονται αναλόγως προς την εναλλασσόμενη αρμονική σειρά και συγκλίνουν σε ένα ποσό χωρίς να είναι απολύτως συγκλίνουσα . Γενικά, δεν είναι δυνατόν να γραφεί ο αντίστροφος μετασχηματισμός ως ολοκλήρωμα Lebesgue . Ωστόσο, όταν οι δύο f και ƒ είναι ολοκληρώσιμες, η αντίστροφη ισότητα
ισχύει σχεδόν παντού . Δηλαδή, ο μετασχηματισμός Fourier είναι injective την L 1 ( R ) . (Αλλά αν f είναι συνεχής, τότε ισχύει η ισότητα για κάθε x .)
Το θεώρημα Plancherel και το θεώρημα του Parseval[Επεξεργασία | επεξεργασία κώδικα]
Έστω f(x) και g(x) είναι ολοκληρώσιμες, και το f (ξ) και είναι ο μετασχηματισμός Fourier τους. Αν f ( x ) και g ( x ) είναι επίσης ολοκληρώσιμες τότε έχουμε το θεώρημα του Parseval ( Rudin 1987 , σ. 187.):
όπου η γραμμή υποδηλώνει το μιγαδικό συζυγή.
Το θεώρημα Plancherel, το οποίο είναι ισοδύναμο με το θεώρημα του Parseval , αναφέρει ( Rudin 1987 , σ. 186.):
Το θεώρημα Plancherel καθιστά δυνατή την επέκταση του μετασχηματισμού Fourier, με το επιχείρημα της συνέχειας, σε έναν ενιαίο φορέα για L2(R). Στις 'L1(R)∩L2(R), η επέκταση αυτή συμφωνεί με την αρχή μετασχηματισμού Fourier που ορίζεται στο L1(R),διευρύνοντας έτσι το πεδίο του μετασχηματισμού Fourier στο L1(R) + L2(R) (και κατά συνέπεια,Lp(R) for 1 ≤ p ≤ 2).Το Plancherel θεώρημα έχει την ερμηνεία των επιστημών ότι ο μετασχηματισμός Fourier διατηρεί την ενέργεια της αρχικής ποσότητας. Ανάλογα με τον συγγραφέα, αυτά τα θεωρήματα θα μπορούσε να αναφέρεται ως Plancherel θεώρημα ή ως θεώρημα του Parseval.
Τύπος άθροισης Poisson[Επεξεργασία | επεξεργασία κώδικα]
Ο τύπος άθροισης Poisson (PSF) είναι μια εξίσωση που συσχετίζει τους συντελεστές της σειράς Fourier του περιοδικού αθροίσματος μιας συνάρτησης με τις τιμές της συνεχούς συνάρτησης του Fourier μετασχηματισμού. Έχει μια ποικιλία χρήσιμων μορφών που προέρχονται από τη βασική μία με εφαρμογή στην κλιμάκωση του μετασχηματισμού Fourier και στην χρονική μετατόπιση των ιδιοτήτων. Η διπλή συχνότητα του προτύπου PSF καλείται επίσης διακριτού χρόνου μετασχηματισμός Fourier, η οποία οδηγεί απευθείας σε:
- μια δημοφιλή γραφική συχνότητα αναπαράστασης του φαινομένου aliasing και
- μια απόδειξη του θεωρήματος δειγματοληψίας Nyquist-Shannon.
Θεώρημα συνέλιξης[Επεξεργασία | επεξεργασία κώδικα]
Ο μετασχηματισμός Fourier μεταφράζεται μεταξύ έλικας και πολλαπλασιασμού των συναρτήσεων. Αν και είναι ολοκληρώσιμες συναρτήσεις με μετασχηματισμό Fourier και αντίστοιχα, τότε ο μετασχηματισμός Fourier της ανελίξεως δίνεται από το γινόμενο των μετασχηματισμών Fourier και (υπό άλλες συνθήκες για τον ορισμό του μετασχηματισμού Fourier μπορεί να εμφανιστεί ένας σταθερός παράγοντας).
Αυτό σημαίνει ότι, εάν:
- όπου το δηλώνει την πράξη της συνέλιξης, τότε:
Στο γραμμικό χρονικά αναλλοίωτο (ΓΧΑ) σύστημα, είναι σύνηθες να ερμηνευθεί η ως κρουστική απόκριση ενός ΓΧΑ συστήματος με είσοδο και την έξοδο , δεδομένου ότι η υποκατάσταση της μονάδας ώθηση για το είναι η . Στην περίπτωση αυτή, αντιπροσωπεύει την απόκριση συχνότητας του συστήματος.
Αντιστρόφως, εάν μπορεί να αναλυθεί ως το προϊόν των δύο τετραγωνικών ολοκληρώσιμων συναρτήσεων και , τότε ο μετασχηματισμός Fourier της δίδεται από τη συνέλιξη των αντίστοιχων μετασχηματισμών Fourier and .
Θεώρημα Συσχέτισης[Επεξεργασία | επεξεργασία κώδικα]
Με ανάλογο τρόπο, μπορεί να δειχθεί ότι αν είναι η συσχέτιση της και :
τότε ο μετασχηματισμός Fourier της h(x) είναι:
Ως ειδική περίπτωση, η αυτοσυσχέτιση της συνάρτησης f(x) είναι:
για τις οποίες
Ερμιτιανές συναρτήσεις[Επεξεργασία | επεξεργασία κώδικα]
Μία σημαντική επιλογή μιας ορθοκανονικής βάσης για το δίνεται από τις συναρτήσεις Hermite
όπου Hen(x) είναι η "probabilist" του Hermite πολυωνύμου , που ορίζεται από
Σύμφωνα με αυτή τη σύμβαση για το μετασχηματισμό Fourier, έχουμε ότι
- .
Με άλλα λόγια, οι συναρτήσεις Hermite αποτελούν ένα πλήρες ορθοκανονικό σύστημα ιδιοσυναρτήσεων για το μετασχηματισμό Fourier για (( Pinsky 2002 ).Ωστόσο, αυτή η επιλογή δεν είναι μοναδική. Υπάρχουν μόνο τέσσερις διαφορετικές ιδιοτιμές του μετασχηματισμού Fourier(±1 and ±i) και κάθε γραμμικός συνδυασμός των ιδιοσυναρτήσεων με την ίδια ιδιοτιμή δίνει μια άλλη ιδιοσυνάρτηση.Ως συνέπεια αυτού, είναι δυνατόν να αποσυντεθούν ως άμεσο άθροισμα των τεσσάρων χώρων H0, H1, H2, και H3 όπου ο μετασχηματισμός Fourier δρα Hek απλά με πολλαπλασιασμό ik.
Δεδομένου ότι το πλήρες σύνολο των Hermite συναρτήσεων παρέχει μια ανάλυση της ταυτότητας, ο μετασχηματισμός Fourier μπορεί να εκπροσωπείται από ένα τέτοιο σύνολο των όρων που σταθμίζονται από τις παραπάνω ιδιοτιμές, και τα ποσά αυτά μπορεί άμεσα να αθροίζονται. Αυτή η προσέγγιση για να καθοριστεί ο μετασχηματισμός Fourier οφείλεται στο Ν. Wiener ( Duoandikoetxea 2001 ).Μεταξύ άλλων ιδιοτήτων,οι Hermite συναρτήσεις μειώνονται εκθετικά γρήγορα τόσο σε συχνότητα όσο και σε χρόνο, και είναι ως εκ τούτου χρήσιμο για να καθοριστεί μια γενίκευση του μετασχηματισμού Fourier, δηλαδή ο κλασματικός μετασχηματισμό Fourier που χρησιμοποιείται στην ανάλυση χρόνου-συχνότητας ( Boashash 2003 ). Στη φυσική, εισήχθη από Condon ( Condon 1937 ).
Μετασχηματισμός Fourier στον Ευκλείδιο χώρο[Επεξεργασία | επεξεργασία κώδικα]
Ο μετασχηματισμός Fourier μπορεί να είναι σε οποιοδήποτε αυθαίρετο αριθμό διαστάσεων n . Όπως και με την μονοδιάστατη περίπτωση, υπάρχουν πολλές περιπτώσεις. Για μια ολοκληρώσιμη συνάρτηση f(x), παίρνουμε τον ορισμό:
όπου x και ξ είναι n-διάστατα διανύσματα,και x · ξ είναι το γινόμενο των διανυσμάτων. Το εσωτερικό γινόμενο μερικές φορές γράφεται ως . Όλες οι βασικές ιδιότητες που αναφέρονται παραπάνω ισχύουν και για τον n -διαστάσεων μετασχηματισμό Fourier, όπως και του Plancherel και το Θεώρημα Parseval. Όταν η συνάρτηση είναι ολοκληρώσιμη, ο μετασχηματισμός Fourier εξακολουθεί να είναι ομοιόμορφα συνεχής και Riemann-Lebesgue. ( Stein & Weiss 1971 )
Αρχή της αβεβαιότητας[Επεξεργασία | επεξεργασία κώδικα]
Σε γενικές γραμμές, όσο πιο πυκνή είναι η f(x) τόσο πιο απλωμένος πρέπει να είναι ο μετασχηματισμός Fourier της ƒ (ξ). Συγκεκριμένα, η ιδιότητα κλιμάκωση του μετασχηματισμού Fourier μπορεί να θεωρηθεί ως ρητό: αν "συμπιεστεί" μια συνάρτηση στο x ο μετασχηματισμός Fourier της "απλώνεται" σε ξ. Δεν είναι δυνατόν να ορισθεί αυθαίρετα μια συνάρτηση του μετασχηματισμού Fourier.
Η συμπίεση της συνάρτησης του μετασχηματισμού Fourier μπορεί να επισημοποιηθεί με τη μορφή της αρχής της αβεβαιότητας από την προβολή μιας συνάρτησης του μετασχηματισμού Fourier ως συζευγμένο μεταβλητές σε σχέση με την συμπλεκτική μορφή στο πεδίο του χρόνου-συχνότητας : από την άποψη του γραμμικού κανονιστικού μετασχηματισμού , ο μετασχηματισμός Fourier περιστρέφεται κατά 90 ° στο πεδίο χρόνου-συχνότητας, και διατηρεί την συμπλεκτική μορφή .
Ας υποθέσουμε ότι f(x)είναι μια ολοκληρώσιμη τετραγωνική συνάρτηση. Χωρίς βλάβη της γενικότητας, υποθέτουμε ότι f(x) είναι η κανονικοποιημένη:
Όπως προκύπτει από την Plancherel θεώρημα ότι η ƒ(ξ) επίσης κανονικοποιείται.
Η εξάπλωση γύρω από x = 0 μπορεί να μετρηθεί με τη διασπορά περίπου μηδέν ( Pinsky του 2002 , σελ. 131.) που ορίζεται από
Όσον αφορά την πιθανότητα, αυτή η δεύτερη τιμή της |f(x)|2 περίπου μηδέν.
Αν f(x) δεν είναι απολύτως συνεχής και οι συναρτήσεις x·f(x) και f′(x) είναι τετραγωνικά ολοκληρώσιμες, τότε
- (Pinsky 2002).
Η ισότητα επιτυγχάνεται μόνο στην περίπτωση που (ως εκ τούτου) όπου σ> 0 και C1 τέτοια ώστε η f να είναι L2–normalized (Pinsky 2002).Με άλλα λόγια, όπου f είναι μια (κανονικοποιημένη) Gaussian συνάρτηση με τη διακύμανση σ2,κοντά στο μηδέν, και ο μετασχηματισμός Fourier του είναι μια Gaussian συνάρτηση με τη διακύμανση σ−2.
Στην πραγματικότητα, αυτή η ανισότητα συνεπάγεται ότι:
για κάθε x0, ξ0 ∈ R (Stein & Shakarchi 2003, σελ. 158).
Στην κβαντική μηχανική , η δυναμική και η θέση των κυματοσυναρτήσεων είναι ζεύγη μετασχηματισμού Fourier,ενός παράγοντα σταθεράς του Planck . Με αυτά λαμβάνοντας υπόψη,την ανισότητα από πάνω έχουμε την αρχής της αβεβαιότητας του Heisenberg ( Stein & Shakarchi 2003 , p. 158).
Μια ισχυρότερη αρχή της αβεβαιότητας είναι η αρχή της αβεβαιότητας του Hirschman η οποία εκφράζεται ως:
όπου H(p) είναι η διαφορική εντροπία της πυκνότητας συνάρτησης πιθανότητας p(x):
όπου οι λογάριθμοι μπορεί να είναι σε οποιαδήποτε βάση η οποία είναι συνεχής. Η ισότητα επιτυγχάνεται για μια Gaussian, όπως και στην προηγούμενη περίπτωση.
Σφαιρικές αρμονικές[Επεξεργασία | επεξεργασία κώδικα]
Αν το σύνολο των ομοιογενών αρμονικών πολυωνύμων βαθμού k στον Rn συμβολίζεται με Ak.Το σύνολο Ak αποτελείται από τις στερεές σφαιρικές αρμονικές βαθμού k.Οι συμπαγείς σφαιρικές αρμονικές διαδραματίζουν παρόμοιο ρόλο σε υψηλότερες διαστάσεις των Hermite πολυωνύμων στη μία διάσταση.Συγκεκριμένα, εάν f(x) = e−π|x|2P(x) για κάποιο P(x) στο Ak, τότε . Αν το σύνολο Hk είναι το κλείσιμο στο L2(Rn) των γραμμικών συνδυασμών των συναρτήσεων της μορφής f(|x|)P(x), όπουP(x) είναι ένα Ak. Ο χώρος L2(Rn)είναι στη συνέχεια ένα άμεσο άθροισμα των χώρων Hk και ο μετασχηματισμός Fourier σε κάθε χώρο Hk στον εαυτό του και είναι δυνατόν να χαρακτηριστεί ως η δράση του μετασχηματισμού Fourier σε κάθε χώρο Hk( Stein & Weiss 1971, ). Έστω f(x) = f0(|x|)P(x) (with P(x) σε ένα Ak),τότε τότε όταν
Εδώ J(n + 2k − 2)/2 υποδηλώνει τη συνάρτηση Bessel του πρώτου είδους με (n + 2k − 2)/2. Όταν k = αυτό δίνει μια χρήσιμη φόρμουλα για το μετασχηματισμό Fourier μιας ακτινική συνάρτηση ( Γραφάκος 2004 ).
Άλλες συμβάσεις[Επεξεργασία | επεξεργασία κώδικα]
Ο μετασχηματισμός Fourier μπορεί επίσης να γραφτεί από την άποψη της γωνιακής συχνότητας :ω = 2πξ των οποίων οι μονάδες είναι ακτίνια ανά δευτερόλεπτο.
Η υποκατάσταση ξ = ω / (2π) στους παραπάνω τύπους παράγει αυτή τη σύμβαση:
Σύμφωνα με αυτή τη σύμβαση, ο αντίστροφος μετασχηματισμός γίνεται:
Σε αντίθεση με την σύμβαση που ακολουθείται σε αυτό το άρθρο, όταν ο μετασχηματισμός Fourier ορίζεται με αυτόν τον τρόπο, δεν είναι πλέον ένας μοναδιαίος μετασχηματισμός στο L2(Rn). Υπάρχει επίσης λιγότερη συμμετρία μεταξύ των τύπων για τον μετασχηματισμό Fourier και αντίστροφο του.
Μια άλλη σύμβαση είναι να χωριστεί ο συντελεστής (2π)n ισομερώς μεταξύ του μετασχηματισμού Fourier και το αντίστροφο, γεγονός που οδηγεί σε ορισμούς:
Σύμφωνα με αυτή τη σύμβαση, ο μετασχηματισμός Fourier είναι και πάλι ένας μοναδιαίος μετασχηματισμός στον L2(Rn). Επαναφέρει επίσης τη συμμετρία μεταξύ του μετασχηματισμού Fourier και το αντίστροφο.
Παραλλαγές των τριών συμβάσεων μπορεί να δημιουργηθεί με σύζευξη του συμπλόκου-εκθετική πυρήνα τόσο ως της προς τα εμπρός ως και της αντίστροφης μετατροπής. Τα σύμβολα πρέπει να είναι αντίθετα. Εκτός από αυτό, η επιλογή είναι (και πάλι) θέμα σύμβασης.
| συνήθη συχνότητα ξ (hertz) | ενιαίου |
|
|---|---|---|
| γωνιακή συχνότητα ω (rad/s) | μη ενιαίου |
|
| ενιαίου |
|
Όπως συζητήθηκε παραπάνω, η χαρακτηριστική λειτουργία μιας τυχαίας μεταβλητής είναι το ίδιο με το Fourier-Stieltjes μετασχηματισμού μέτρου διανομής της, αλλά σε αυτό το πλαίσιο, είναι σύνηθες να λάβει διαφορετική σύμβαση για την σταθερές.
Τυπικά χαρακτηριστική συνάρτηση ορίζεται .
Όπως και στην περίπτωση του «μη-ενιαία γωνιακή συχνότητα" σύμβαση παραπάνω, δεν υπάρχει παράγοντας που περιλαμβάνεται στο 2π είτε του ολοκληρώματος ή στην εκθετική. Σε αντίθεση με οποιαδήποτε από τις συμβάσεις που παρουσιάζεται πιο πάνω, αυτή η σύμβαση έχει το αντίθετο πρόσημο στην εκθετική.
Πίνακες σημαντικών Fourier μετασχηματισμών[Επεξεργασία | επεξεργασία κώδικα]
Οι παρακάτω πίνακες καταγράφουν κάποια κλειστή μορφή μετασχηματισμών Fourier. Για τις συναρτήσεις 'f(x), g(x) και h(x)οι μετασχηματισμοί Fourier είναι ƒ, , και αντίστοιχα.Περιλαμβάνονται μόνο οι τρεις πιο κοινές συμβάσεις. Μπορεί να είναι χρήσιμο να παρατηρήσετε ότι η είσοδος 105 δίνει μια σχέση μεταξύ του μετασχηματισμού Fourier μιας συνάρτησης και της αρχικής λειτουργίας, το οποίο μπορεί να θεωρηθεί ως αφορούν το μετασχηματισμό Fourier και αντίστροφο του.
Σχέσεις συναρτήσεων[Επεξεργασία | επεξεργασία κώδικα]
Ο μετασχηματισμός Fourier του πίνακα αυτού μπορεί να βρεθεί στο Erdélyi (1954 ) ή Kammler (2000 , παράρτημα).
| Συνάρτηση | Μετασχηματισμός Fourier ενιαία, τακτική συχνότητα |
Μετασχηματισμός Fourier ενιαία, γωνιακή συχνότητα |
Μετασχηματισμός Fourier μη ενιαία, γωνιακή συχνότητα |
Παρατηρήσεις | |
|---|---|---|---|---|---|
|
|
|
|
Ορισμός | ||
| 101 | Γραμμικότητα | ||||
| 102 | Στροφή στο πεδίο του χρόνου | ||||
| 103 | Στροφή στο πεδίο συχνοτήτων, η διπλή από 102 | ||||
| 104 | Κλιμάκωση στο πεδίο του χρόνου.Εάν είναι μεγάλο,τότε είναι συγκεντρωμένη γύρω από μηδέν και . | ||||
| 105 | Εδώ πρέπει να υπολογιστεί χρησιμοποιώντας την ίδια μέθοδο όπως στήλη μετασχηματισμού Fourier. Τα αποτελέσματα από την εναλλαγή "εικονικών" μεταβλητών του x και ξ ή ω ή μ. | ||||
| 106 | |||||
| 107 | Αυτή είναι η διπλή από 106 | ||||
| 108 | Ο συμβολισμός υποδηλώνει τη συνέλιξη των f και g — ο κανόνας αυτός είναι το θεώρημα συνέλιξης convolution theorem | ||||
| 109 | Αυτή είναι η διπλή από 108 | ||||
| 110 | Για καθαρά πραγματική | Hermitian συμμετρία. δείχνει το συζυγή μιγαδικό . | |||
| 111 | Για καθαρά πραγματική | , και είναι καθαρά πραγματικές συναρτήσεις | |||
| 112 | Για καθαρά πραγματική περιττή | , και είναι καθαρά φανταστικές περιττές συναρτήσεις . | |||
Τετραγωνικές Ολοκληρώσιμες Συναρτήσεις[Επεξεργασία | επεξεργασία κώδικα]
Ο μετασχηματισμός Fourier του πίνακα αυτού μπορεί να βρεθεί στο ( Campbell & Foster 1948 ), ( Erdélyi 1954 ), ή το προσάρτημα του ( Kammler 2000 ).
| Συνάρτηση | Μετασχηματισμός Fourier ενιαία, τακτική συχνότητα |
Μετασχηματισμός Fourier ενιαία, γωνιακή συχνότητα |
Μετασχηματισμός Fourier μη-ενιαία, γωνιακή συχνότητα |
Παρατηρήσεις | |
|---|---|---|---|---|---|
|
|
|
|
|||
| 201 | Ο ορθογώνιος παλμός και η κανονικοποιημένη συνάρτηση sinc , εδώ ορίζεται ως sinc(x) = sin(πx)/(πx) | ||||
| 202 | Διπλή του άρθρου 201. Η ορθογώνια λειτουργία είναι ένα ιδανικό βαθυπερατό φίλτρο , και το sinc λειτουργία είναι η μη-αιτιώδης παλμική απόκριση ενός τέτοιου φίλτρου. | ||||
| 203 | Η συνάρτηση tri(x) είναι η συνάρτηση τριγωνικό | ||||
| 204 | Διπλή του άρθρου 203 του Κανονισμού. | ||||
| 205 | Η συνάρτηση u(x) είναι η μοναδιαία βηματική συνάρτηση Heaviside και a>0. | ||||
| 206 | Αυτό δείχνει οτι , για τον ενιαίο μετασχηματισμό Fourier, ηGaussian συνάρτηση exp(−αx2) έχει το δικό της μετασχηματισμό Fourier για κάποιες τιμές τουα. Για να είναι και ολοκληρώσιμη πρέπει να έχει Re(α)>0. | ||||
| 207 | Για a>0. Δηλαδή ο μετασχηματισμός Fourier μιας εκθετικής συνάρτησης είναι μια Lorentzian συνάρτηση. | ||||
| 208 | Υπερβολικές συναρτήσεις έχουν το δικό τους μετασχηματισμό Fourier | ||||
| 209 |
|
|
|
είναι το πολυώνυμο Hermite . Εάν a = 1 τότε οι Gauss-Hermite συναρτήσεις είναι ερμιτιανές με μετασχηματισμό Fourier. Για την παραγωγή, βλέπε πολυώνυμο Hermite . Ο τύπος μειώνει έως 206 γιαn = 0. |
Διανομές[Επεξεργασία | επεξεργασία κώδικα]
Ο μετασχηματισμός Fourier του πίνακα αυτού μπορεί να βρεθεί στο ( Erdélyi 1954 ) ή το προσάρτημα του ( Kammler 2000 ).
| Συνάρτηση | Μετασχηματισμός Fourier ενιαία, τακτική συχνότητα |
Μετασχηματισμός Fourier ενιαία, γωνιακή συχνότητα |
Μετασχηματισμός Fourier μη-ενιαία, γωνιακή συχνότητα |
Παρατηρήσεις | ||
|---|---|---|---|---|---|---|
|
|
|
|
||||
| 301 | Η κατανομή δ(ξ)είναι η συνάρτηση δ του Dirac . | |||||
| 302 | Διπλή του κανόνα 301. | |||||
| 303 | Αυτό προκύπτει από το 103 και το 301. | |||||
| 304 | Αυτό προκύπτει από τους κανόνες 101 και 303 με τον τύπο του Euler :
| |||||
| 305 | Αυτό προκύπτει από το 101 και 303 με
| |||||
| 306 | ||||||
| 307 | ||||||
| 308 | Εδώ,το n είναι ένας φυσικός αριθμός και είναι n-οστή παράγωγο διανομής της συνάρτησης Dirac δέλτα. Ο κανόνας αυτός προκύπτει από τους κανόνες 107 και 301. Συνδυάζοντας τον κανόνα αυτό με 101, μπορούμε να μετατρέψουμε όλα τα πολυώνυμα . | |||||
| 309 | Εδώ sgn(ξ) είναι η sign συνάρτηση. Σημειώστε ότι 1/x δεν είναι μια διανομή. Είναι απαραίτητο να χρησιμοποιήσετε την αξία του Cauchy όταν πραγματοποιούνται δοκιμές έναντι Schwartz συναρτήσεων. Αυτός ο κανόνας είναι χρήσιμος στη μελέτη του μετασχηματισμού Hilbert . | |||||
| 310 |
|
1/xn είναι η ομοιογενής κατανομή ορίζεται από το διανεμητικά παραγώγου | ||||
| 311 | Ο τύπος αυτός ισχύει για 0 > α > −1. Για α > 0 κάποιοι όροι προκύπτουν κατά την προέλευσή τους, που μπορεί να βρεθεί με τη διαφοροποίηση 318. Εάν Re α > −1, τότε είναι μια τοπικά ολοκληρώσιμη συνάρτηση . Η συνάρτηση είναι μία αναλυτική συνάρτηση από το δεξιά ημιεπίπεδο στο χώρο της διανομής. Μια μοναδική meromorphic επέκταση διανομής, επίσης, συμβολίζεται με για α ≠ −2, −4, ... (Βλέπε ομοιογενή κατανομή .) | |||||
| 312 | Το διπλό του 309 κανόνα. Αυτή τη φορά ο μετασχηματισμός Fourier θα πρέπει να θεωρηθεί ως Cauchy. | |||||
| 313 | Η συνάρτηση u(x) είναι μοναδιαία βηματική συνάρτηση Heaviside. Αυτό προκύπτει από τους κανόνες 101, 301, και 312. | |||||
| 314 | Αυτή η συνάρτηση είναι γνωστή ως η Dirac συνάρτηση. Αυτό το αποτέλεσμα μπορεί να προέλθει από 302 και 102, σε συνδυασμό με το γεγονός ότι ως διανομές. | |||||
| 315 | Η συνάρτηση J0(x)είναι μηδενικής τάξης Bessel συνάρτηση πρώτου είδους. | |||||
| 316 | Αυτό είναι μια γενίκευση των 315. Η συνάρτηση Jn(x) είναι η n-οστής τάξης Bessel συνάρτηση πρώτου είδους.Η συνάρτηση Tn(x)είναι το πολυώνυμο Chebyshev του πρώτου είδους . | |||||
| 317 | είναι η Euler-Mascheroni σταθερά . | |||||
| 318 | Ο τύπος αυτός ισχύει για 1 > α > 0. Χρησιμοποιώντας τους τύπους για διαφορετικούς εκθέτες. u είναι η συνάρτηση μοναδιαία βηματική συνάρτηση Heaviside. |
Δύο διαστάσεων συναρτήσεις[Επεξεργασία | επεξεργασία κώδικα]
| Συνάρτηση | Μετασχηματισμός Fourier ενιαία, τακτική συχνότητα |
Μετασχηματισμός Fourier ενιαία, γωνιακή συχνότητα |
Μετασχηματισμός Fourier μη-ενιαία, γωνιακή συχνότητα | |
|---|---|---|---|---|
| 400 |
|
|
| |
| 401 | ||||
| 402 |
- Παρατηρήσεις
Σε 400: Οι μεταβλητές ξx, ξy, ωx, ωy, νx και νy είναι πραγματικοί αριθμοί.
Τα ολοκληρώματα που λαμβάνονται ισχύουν από παραπάνω.
Σε 401: Και οι δύο συναρτήσεις είναι Gaussians, οι οποίες δεν μπορεί να έχουν μονάδα όγκου.
Σε 402: Η συνάρτηση που ορίζεται από κυκλ(r)=1 0≤r≤1,0 είναι διαφορετικά.Αυτή είναι η κατανομή Airy ,και εκφράζεται με τη χρήση J1 (η τάξης 1 συνάρτηση Bessel του πρώτου είδους). ( Stein & Weiss 1971 , THM. IV.3.3)
Γενικοί τύποι για n-διάστατες συναρτήσεις[Επεξεργασία | επεξεργασία κώδικα]
| Συνάρτηση | Μετασχηματισμός Fourier ενιαία, τακτική συχνότητα |
Μετασχηματισμός Fourier ενιαία, γωνιακή συχνότητα |
Μετασχηματισμός Fourier μη-ενιαία, γωνιακή συχνότητα | |
|---|---|---|---|---|
| 500 |
|
|
| |
| 501 | ||||
| 502 |
- Παρατηρήσεις
To 501: Η συνάρτηση χ[0,1] είναι η συνάρτηση δείκτη του διαστήματος [0, 1]. Η συνάρτηση Γ(x) είναι η συνάρτηση γάμμα. Η συνάρτηση Jn/2 + δ είναι μια συνάρτηση Bessel πρώτου είδους, με τάξη n/2 + δ. Λαμβάνοντας n = 2 καιδ = 0 παράγει την 402. (Stein & Weiss 1971 , THM. 4.15)
To 502: Δείτε δυναμικό Riesz. Ο τύπος ισχύει επίσης και για όλα τα α ≠ −n, −n − 1, ... από την αναλυτική συνέχιση, αλλά στη συνέχεια η συνάρτηση του μετασχηματισμού Fourier πρέπει να γίνει αντιληπτή από τις κατάλληλες διανομές. Βλέπε ομοιογενή κατανομή.































![{\displaystyle {\mathcal {P}}[f]\colon t\mapsto f(-t),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bbe49057a4072d0faa2a0e4b8046d81066e767db)






















































































































































































































































![{\displaystyle \displaystyle \chi _{[0,1]}(|x|)(1-|x|^{2})^{\delta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6c42190ce04a2aacb193c4460aab695ee32ec977)







