Κατανομή Πουασσόν


| Συμβολισμός | |
| Παράμετροι | |
| Φορέας | |
| Συνάρτηση Μάζας Πιθανότητας |
|
| Μέσος | |
| Διάμεσος | , |
| Διακύμανση | |
| Λοξότητα | |
| Κύρτωση | |
| Εντροπία | |
| Ροπή | |
| Πιθανογεννήτρια | |
| Χαρακτηριστική |
Στην θεωρία πιθανοτήτων και στατιστικής, η κατανομή Poisson, η οποία πήρε το όνομά της από τον Γάλλο μαθηματικό Siméon Denis Poisson, είναι μία διακριτή συνάρτηση κατανομής που εκφράζει την πιθανότητα ενός δεδομένου αριθμού γεγονότων που συμβαίνουν σε ένα σταθερό διάστημα χρόνου ή/και χώρου αν αυτά τα γεγονότα συμβαίνουν με ένα γνωστό μέσο ρυθμό και είναι ανεξάρτητα από το χρονικό διάστημα από την τελευταία περίπτωση.[1] Η κατανομή Poisson μπορεί επίσης να χρησιμοποιηθεί για τον αριθμό γεγονότων σε άλλα καθορισμένα διαστήματα όπως η απόσταση, η επιφάνεια ή ο όγκος.
Για παράδειγμα, ας υποθέσουμε ότι κάποιος παίρνει 4 αλληλογραφίες ημερησίως κατά μέσο όρο. Θα υπάρξει, ωστόσο, μία ορισμένη διάδοση: μερικές φορές λίγα περισσότερα, μερικές φορές λίγο λιγότερα, πότε-πότε τίποτα.[2] Δεδομένου μόνο του μέσου ρυθμού, για ένα ορισμένο διάστημα παρακολούθησης (αριθμό αλληλογραφίας ανά μέρα, τηλεφωνήματα ανά ώρα, κτλ.), και υποθέτοντας ότι η διαδικασία, ή ο συνδυασμός των διαδικασιών , που παράγουν τα γεγονότα είναι ουσιαστικά τυχαίος, η κατανομή Poisson καθορίζει πόσο πιθανό είναι ότι ο αριθμός θα είναι 3, ή 5, ή 10, ή κάποιος άλλος αριθμός, κατά την διάρκεια μίας περιόδου παρατήρησης. Αυτό σημαίνει ότι, προβλέπει τον αριθμό διάδοσης γύρω από ένα γνωστό ρυθμό εξάπλωσης .[2]
Η κατανομή Poisson έχει την παράμετρο λ που δηλώνει τη μέση τιμή αριθμού εμφανίσεων ενός γεγονότος, οι οποίες είναι ανεξάρτητες της τελευταίας χρονικής στιγμής εμφάνισης του γεγονότος.
Ιστορία[Επεξεργασία | επεξεργασία κώδικα]
Η κατανομή εισήχθει αρχικά από τον Siméon Denis Poisson (1781–1840) και δημοσιεύθηκε, μαζί με την θεωρία πιθανότητας του, το 1837 στο Recherches sur la probabilité des jugements en matière criminelle et en matière civile (“Έρευνα σχετικά με την Πιθανότητα αποφάσεων σε ποινικές και αστικές υποθέσεις”).[3] Το έργο ασχολείται με τον αριθμό των άδικων καταδικών σε μια δεδομένη χώρα εστιάζοντας σε ορισμένες τυχαίες μεταβλητές N που μετρούν, μεταξύ των άλλων, τον αριθμό διακεκριμένων περιστατικών (μερικές φορές αποκαλούμενων "γεγονότα" ή “αφίξεις”) που πραγματοποιούνται κατά την διάρκεια ενός χρόνου-διαστήματος δεδομένου μήκους. Τα αποτελέσματα είχαν δοθεί παλαιότερα από τον Abraham de Moivre (1711) στο De Mensura Sortis seu; de Probabilitate Eventuum in Ludis a Casu Fortuito Pendentibus in Philosophical Transactions of the Royal Society, p. 219.[4]
Μία πρακτική εφαρμογή αυτής της κατανομής έγινε από τον Ladislaus Bortkiewicz το 1898 όταν του δόθηκε η εργασία να διερευνήσει τον αριθμό των στρατιωτών του Πρωσικού στρατού που σκοτώθηκαν κατά λάθος από κλωτσιά αλόγου; αυτό το πείραμα εισήγαγε την κατανομή Poisson στον τομέα της εφαρμοσμένης μηχανικής αξιοπιστίας.[5]
Ορισμός[Επεξεργασία | επεξεργασία κώδικα]
Μία διακριτή τυχαία μεταβλητή X ακολουθεί κατανομή Poisson με παράμετρο λ > 0, αν, για k =0,1,2,…, η συνάρτηση πυκνότητας πιθανότητας του X δίνεται από:[6]
όπου
- e είναι ο αριθμός του Euler (e = 2.71828...)
- k! είναι το παραγοντικό του k.
Ο θετικός πραγματικός αριθμός λ είναι ίσος με την αναμενόμενη τιμή του X και επίσης της διακύμανσης[7]
Η κατανομή Poisson μπορεί να εφαρμοστεί σε συστήματα με μεγάλο αριθμό πιθανών γεγονότων, καθένα από τα οποία είναι σπάνια. Πόσα τέτοια γεγονότα θα συμβούν κατά την διάρκεια ενός τέτοιου χρονικού διαστήματος; Υπό τις κατάλληλες συνθήκες, αυτός είναι ένας τυχαίος αριθμός με κατανομή Poisson.
Μέση τιμή[Επεξεργασία | επεξεργασία κώδικα]
Από τον ορισμό της μέσης τιμής, έχουμε ότι:
Διακύμανση[Επεξεργασία | επεξεργασία κώδικα]
Έχουμε ότι:
Από τον τύπο για την διακύμανση έχουμε ότι:
Εντροπία[Επεξεργασία | επεξεργασία κώδικα]
Από τον ορισμό της εντροπίας, έχουμε ότι:
Διάμεσος[Επεξεργασία | επεξεργασία κώδικα]
Όρια για την διάμεσο (ν) της κατανομής είναι γνωστά και ακριβή:[8]
Ροπές[Επεξεργασία | επεξεργασία κώδικα]
Οι ανώτερες ροπές mk της Poisson κατανομής σχετικά με την προέλευση είναι πολυώνυμα Touchard του λ:
όπου τα {άγκιστρα} υποδηλώνουν Stirling αριθμούς του δεύτερου είδους.[9] Οι συντελεστές των πολυωνύμων έχουν ένα συνδυαστικό νόημα. Στην πραγματικότητα, όταν η αναμενόμενη τιμή της Poisson κατανομής είναι 1, τότε ο τύπος του Dobinski λέει ότι η n-οστή ροπή ισούται με τον αριθμό των τμημάτων από ένα σύνολο μεγέθους n.
Η n-οστή παραγοντική ροπή της Poisson κατανομής είναι .
| Απόδειξη |
|---|
|
|
Πιθανογεννήτρια συνάρτηση[Επεξεργασία | επεξεργασία κώδικα]
Από τον ορισμό της πιθανογεννήτρια συνάρτηση και έστω :
Χαρακτηριστική συνάρτηση[Επεξεργασία | επεξεργασία κώδικα]
Από τον ορισμό της χαρακτηριστική συνάρτηση και έστω :
Ιδιότητες[Επεξεργασία | επεξεργασία κώδικα]
- Ο συντελεστής διακύμανσης είναι , ενώ ο δείκτης της διασποράς είναι 1.[4]
- Η μέση απόκλιση της μέσης τιμής είναι[4]
- Ο τρόπος μιας τυχαίας μεταβλητής που ακολουθεί Poisson κατανομής με μη ακέραιο λ είναι ίσος με , ο οποίος είναι ο μεγαλύτερος ακέραιος μικρότερος ή ίσος με λ. Αυτό γράφεται επίσης σαν floor(λ). Όταν το λ είναι ένας θετικός ακέραιος, οι τρόποι είναι λ και λ − 1.
- Όλοι οι αθροιστικοί δείκτες της Poisson κατανομής είναι ίσοι με την αναμενόμενη τιμή λ.
- (Άθροισμα κατανομών Πουασσόν) Έστω για ανεξάρτητες τυχαίες μεταβλητές. Τότε , για .[10] Το θεώρημα του Raikov είναι αντίστροφο, το οποίο λέει ότι αν το άθροισμα δύο ανεξάρτητων τυχαίων μεταβλητών είναι Poisson-κατανομή, τότε έτσι είναι και κάθε μία από αυτές τις δύο ανεξάρτητες μεταβλητές.[11]
| Απόδειξη |
|---|
|
Έστω και ανεξάρτητες τυχαίες μεταβλητές. Θεωρώντας την , έχουμε για , χρησιμοποιώντας το διωνυμικό θεώρημα, δλδ . Επομένως, . Χρησιμοποιώντας την μέθοδο της επαγωγής έχουμε ότι . |
- Οι Poisson κατανομές είναι απείρως διαχωρίσιμες κατανομές πιθανότητας.[12][13]
- Η προσανατολισμένη αποκλιση Kullback–Leibler της Pois(λ0) από την Pois(λ) δίνεται από
- Άνω φράγματα μίας ουράς από Poisson τυχαία μεταβλητή μπορεί να προκύψουν χρησιμοποιώντας το Chernoff δεσμευμένο επιχείρημα.[14]
Σχετικές κατανομές[Επεξεργασία | επεξεργασία κώδικα]
- Αν και είναι ανεξάρτητα, τότε η διαφορά ακολουθεί μία Skellam κατανομή.
- Αν και είναι ανεξάρτητα, τότε η κατανομή της εξαρτώμενη από τη είναι μία διωνυμική κατανομή.
Ειδικά, δεδομένου ότι , .
Γενικότερα, αν X1, X2,..., Xn είναι ανεξάρτητες Poisson τυχαίες μεταβλητές με παραμέτρους λ1, λ2,..., λn τότε
- δεδομένου ότι . Στην πραγματικότητα, .
- Αν και η κατανομή της , δεδομένου ότι X = k, είναι μία διωνυμική κατανομή, , τότε η κατανομή της Y ακολουθεί μία Poisson κατανομή . Στην πραγματικότητα, αν , δεδομένου ότι X = k, ακολουθεί μία πολυωνυμική κατανομή, , τότε κάθε ακολουθεί μία ανεξάρτητη Poisson κατανομή .
- Η Poisson κατανομή μπορεί να διαμορφωθεί ως οριακή περίπτωση της διωνυμικής κατανομής καθώς ο αριθμός των δοκιμών πάει στο άπειρο και ο αναμενόμενος αριθμός των επιτυχιών παραμένει σταθερός — δες νόμος των σπάνιων γεγονότων πιο κάτω. Επίσης μπορεί να χρησιμοποιηθεί ως μία προσέγγιση της διωνυμικής κατανομής αν το n είναι επαρκώς μεγάλο και το p είναι επαρκώς μικρό. Υπάρχει ένας κανόνας που λέει ότι η Poisson κατανομή είναι μία καλή προσέγγιση της διωνυμικής κατανομής αν το n είναι τουλάχιστον 20 και το p είναι μικρότερο ή ίσο του 0.05, και μία άριστη προσέγγιση αν n ≥ 100 και np ≤ 10.[15]
- Η Poisson κατανομή είναι μία ειδική περίπτωση της γενικευμένης stuttering Poisson κατανομής (ή stuttering Poisson κατανομής) με μόνο μία παράμετρο.[16] Η stuttering Poisson κατανομή μπορεί να συναχθεί από την οριακή κατανομή της μονοπαραγοντικής πολυωνυμικής κατανομής. Είναι επίσης μία ειδική περίπτωση από μία σύνθετη Poisson κατανομή.
- Για επαρκώς μεγάλες τιμές του λ, (πες λ>1000), η κανονική κατανομή με μέση τιμή λ και διασπορά λ (τυπική απόκλιση ) είναι μία άριστη προσέγγιση της Poisson κατανομής. Αν το λ είναι μεγαλύτερο από 10 περίπου, τότε η κανονική κατανομή είναι μία καλή προσέγγιση αν εφαρμοστεί η κατάλληλη διόρθωση συνεχείας, δηλαδή, η P(X ≤ x), όπου το(πεζό) x είναι ένας μη-αρνητικός ακέραιος, αντικατασταθεί από P(X ≤ x + 0.5).
- Διασπορά-μετασχηματισμοί σταθεροποίησης: Όταν μία μεταβλητή ακολουθεί Poisson κατανομή, η τετραγωνική της ρίζα ακολουθεί προσεγγιστικά κανονική κατανομή με αναμενόμενη τιμή περίπου and variance of about 1/4.[17],[18] Στο πλαίσιο αυτού του μετασχηματισμού, η σύγκλιση στην κανονικότητα (καθώς το λ αυξάνεται) είναι πολύ πιο γρήγορη από τη μη μετασχηματισμένη μεταβλητή.[εκκρεμεί παραπομπή] Άλλοι, λίγο πιο περίπλοκοι, μετασχηματισμοί σταθεροποίησης διασποράς είναι διαθέσιμοι,[18] ένας από αυτούς είναι ο Anscombe μετασχηματισμός. Δες Μετασχηματισμοί δεδομένων (στατιστική) για περισσότερες γενικές χρήσεις των μετασχηματισμών.
- Αν για κάθε t > 0 ο αριθμός των αφίξεων στο χρονικό διάστημα [0,t] ακολουθεί Poisson κατανομή με μέση τιμή λt, τότε η ακολουθία των φορών μεταξύ των αφίξεων είναι ανεξάρτητη και πανομοιότυπα ακολουθώντας εκθετικήκατανομή οι τυχαίες μεταβλητές έχουν μέση τιμή 1/λ.[19]
- Η αθροιστική συνάρτηση κατανομής της Poisson και της χ-τετράγωνο κατανομής σχετίζονται με τους ακόλουθους τρόπους:[20]
- ακέραιος k,
- και[21]
- Η Γεωμετρική Poisson κατανομή είναι ένας συνδυασμός της Γεωμετρικής κατανομής και της κατανομής Poisson, και περιλαμβάνει και τις δύο ως ειδικές περιπτώσεις.[22][23]
- Ας είναι η συνδέουσα τυχαία μεταβλητή, η Ροπογεννήτρια συνάρτηση της Γεωμετρικής Poisson κατανομής είναι
- Ειδικές Περιπτώσεις
- Κατανομή Poisson:
- Γεωμετρική κατανομή:
Εμφάνιση[Επεξεργασία | επεξεργασία κώδικα]
Εφαρμογές της Poisson κατανομής μπορούν να βρεθούν σε πολλούς τομείς που σχετίζονται με την καταμέτρηση:[24]
- Παράδειγμα στην Τηλεπικοινωνία: οι τηλεφωνικές κλήσεις που φτάνουν σε ένα σύστημα.
- Παράδειγμα στην Αστρονομία: τα φωτόνια που φτάνουν σε ένα τηλεσκόπιο.
- Παράδειγμα στη Βιολογία: ο αριθμός των μεταλλάξεων σε ένα κλώνο του DNA ανά μονάδα μήκους.
- Παράδειγμα στη Διαχείριση: οι πελάτες που φθάνουν σε έναν πάγκο ή ένα τηλεφωνικό κέντρο.
- Παράδειγμα Πολιτικών μηχνανικών: τα αυτοκίνητα που φθάνουν στα φώτα τροχαίας.
- Παράδειγμα στη Χρηματοδότηση και ασφάλιση: ο αριθμός των Απωλειών/Απαιτήσεων που συμβαίνουν σε μία δεδομένη χρονική περίοδο του χρόνου.
- Παράδειγμα στη Σεισμολογία σεισμού: ένα ασυμπτωτικό μοντέλο Poisson of σεισμικών ρίσκων για μεγάλους σεισμούς. (Lomnitz, 1994).
- Παράδειγμα στη Ραδιενέργεια: διάσπαση ενός ραδιενεργού πυρήνα.
Η Poisson κατανομή προκύπτει σε σχέση με τις Poisson επεξεργασίες. Εφαρμόζεται σε διάφορα φαινόμενα με διακριτές ιδιότητες (αυτό είναι, εκείνα που μπορούν να συμβούν 0, 1, 2, 3, ... φορές κατά τη διάρκεια μίας δεδομένης περιόδου του χρόνου ή σε μία δεδομένη περιοχή) όποτε η πιθανότητα να συμβεί το φαινόμενο είναι σταθερή στο χρόνο ή χώρο. Παραδείγματα από γεγονότα που μπορούν να μοντελοποιηθούν ως Poisson κατανομή περιλαμβάνουν:
- Ο αριθμός των στρατιωτών που σκοτώνονται από άλογο-κλωτσιές κάθε χρόνο σε κάθε σώμα στο Πρώσος ιππικό. Αυτό το παράδειγμα έγινε γνωστό από ένα βιβλίο του Ladislaus Josephovich Bortkiewicz (1868–1931).
- Ο αριθμός των κυττάρων ζύμης που χρησιμοποιύνται όταν ετοιμάζεται η μπύρα Guinness. Αυτό το παράδειγμα έγινε γνωστό από τον William Sealy Gosset (1876–1937).[νεκρός σύνδεσμος][25]
- Ο αριθμός των τηλεφωνικών κλήσεων που φτάνουν σε ένα τηλεφωνικό κέντρο σε ένα λεπτό. Αυτό το παράδειγμα έγινε γνωστό από τον A.K. Erlang (1878 – 1929).
- Κίνηση στο διαδίκτυο.
- Ο αριθμός των γκολ σε αθλήματα που περιλαμβάνουν δύο αγωνιζόμενες ομάδες.
- Ο αριθμός των θανάτων ετησίως σε μια συγκεκριμένη ηλικιακή ομάδα.
- Ο αριθμός των αλμάτων σε μια τιμή της μετοχής σε ένα δεδομένο χρονικό διάστημα.
- Υπό την παραδοχή της ομοιογένειας, ο αριθμός των φορών που ένας web server είναι προσβάσιμος ανά λεπτό.
- Ο αριθμός των μεταλλάξεων σε ένα δεδομένο τμήμα του DNA μετά από ένα ορισμένο ποσό της ακτινοβολίας.
- Η αναλογία των κυττάρων που θα έχουν μολυνθεί σε μία δεδομένη πολλαπλότητα μόλυνσης.
- Η άφιξη των φωτονίων σε ένα κύκλωμα εικονοψηφίδων σε μία δεδομένη φωταψία και επί ένα δεδομένο χρονικό διάστημα.
- Η στόχευση των V-1 ιπτάμενων βομβών στο Λονδίνο κατά τη διάρκεια του Β' Παγκοσμίου Πολέμου.[26]
Ο Gallagher το 1976 έδειξε ότι οι μετρήσεις των πρώτων αριθμών σε σύντομα χρονικά διαστήματα υπακούουν σε μια κατανομή Poisson υπό την προϋπόθεση μία συγκεκριμένη έκδοση μιας αναπόδεικτης εικασίας του Hardy και του Littlewood είναι αλήθεια.[27]
Παραγωγή της κατανομής Poisson — Ο νόμος των σπάνιων γεγονότων[Επεξεργασία | επεξεργασία κώδικα]
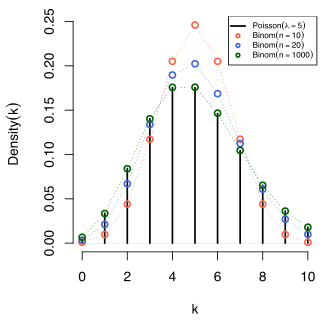
Η κατανομή Poisson μπορεί να παραχθεί θεωρώντας ένα διάστημα, σε χρόνο, χώρο ή αλλιώς, όπου τα γεγονότα συμβαίνουν τυχαία με ένα γνωστό μέσο αριθμό . Το διάστημα χωρίζεται σε υποδιαστήματα ίσου μεγέθους, έτσι ώστε > . Η πιθανότητα ένα γεγονός να πέσει στο υποδιάστημα είναι για κάθε ίση με , και η εμφάνιση ενός γεγονότος στο μπορεί να θεωρηθεί προσεγγιστικά ότι είναι δοκιμή Bernoulli. Ο συνολικός αριθμός των γεγονότων τότε θα είναι ακολουθεί προσεγγιστικά διωνυμική κατανομή με παραμέτρους και Η προσέγγιση θα είναι καλύτερη αυξάνοντας το ; η -κατανομή συγκλίνει στην κατανομή Poisson με παράμετρο στο όριο καθώς το n πλησιάζει το άπειρο.
Σε πολλά από τα παραπάνω παραδείγματα—όπως, ο αριθμός των μεταλλάξεων σε μία δεδομένη ακολουθία του DNA—τα γεγονότα που μετρήθηκαν είναι στην πραγματικότητα τα αποτελέσματα των διακριτών δοκιμών, και θα μπορούσαν να μοντελοποιηθούν με μεγαλύτερη ακρίβεια χρησιμοποιώντας τη διωνυμική κατανομή, που είναι
Σ' αυτές τις περιπτώσεις το n είναι πολύ μεγάλο και το p είναι πολύ μικρό (και η αναμενόμενη τιμή np είναι του ενδιάμεσου μεγέθους). Τότε η κατανομή μπορεί να προσεγγιστεί από τη λιγότερο επαχθή κατανομή Poisson[εκκρεμεί παραπομπή]
Αυτή η προσέγγιση είναι κάποιες φορές γνωστή ως ο νόμος των σπάνιων γεγονότων,[28] καθώς κάθε ένα από τα n μεμονωμένα γεγονότα Bernoulli σπάνια συμβαίνει. Το όνομα μπορεί να είναι παραπλανητικό γιατί ο συνολικός αριθμός των γεγονότων επιτυχίας σε μία Poisson επεξεργασία χρειάζεται να μην είναι σπάνιος αν η παράμετρος np δεν είναι μικρή. Για παράδειγμα, ο αριθμός των τηλεφωνικών κλήσεων σε έναν απασχολημένο πίνακα σε μία ώρα ακολουθεί κατανομή Poisson με τα γεγονότα να εμφανίζονται συχνά στο χειριστή, αλλά είναι σπάνια από την άποψη του μέσου μέλους του πληθυσμού που είναι πολύ απίθανο να πραγματοποιήσει μία κλήση σε εκείνο το τηλεφωνικό κέντρο εκείνη την ώρα.[εκκρεμεί παραπομπή]
Η λέξη νόμος κάποτε χρησιμοποιείται ως συνώνυμο της κατανομής πιθανοτήτων, και σύγκλιση στο νόμο σημαίνει σύγκλιση στην κατανομή. Επομένως, η κατανομή Poisson κάποτε καλείται ο νόμος των μικρών αριθμών γιατί είναι η κατανομή πιθανοτήτων του αριθμού των εμφανίσεων ενός γεγονότος που συμβαίνει σπάνια αλλά έχει πάρα πολλές ευκαιρίες να συμβεί. The Law of Small Numbers είναι ένα βιβλίο από τον Ladislaus Bortkiewicz (Bortkevitch)[29] σχετικά με την κατανομή Poisson, που δημοσιεύτηκε το 1898. Κάποιοι έχουν εισηγηθεί ότι η κατανομή Poisson θα έπρεπε να καλείται κατανομή Bortkiewicz.[30]
Πολυδιάστατη διαδικασία Poisson[Επεξεργασία | επεξεργασία κώδικα]
Η κατανομή Poisson προκύπτει ως η κατανομή των αριθμών των εμφανίσεων των γεγονότων σε (πολυδιάστατα) διαστήματα σε πολυδιάστατες επεξεργασίες Poisson σε έναν απευθείας ισοδύναμο τρόπο στο αποτέλεσμα για μονοδιάστατες επεξεργασίες. Έτσι, αν D είναι οποιαδήποτε περιοχή όπου ο πολυδιάστατος χώρος για τον οποίο |D|, το εμβαδό ή ο όγκος της περιοχής, είναι άπειρο, και αν N(D) είναι καταμέτρηση του αριθμού των γεγονότων στο D, τότε
Άλλες εφαρμογές στην επιστήμη[Επεξεργασία | επεξεργασία κώδικα]
Σε μία επεξεργασία Poisson, ο αριθμός των παρατηρούμενων περιστατικών κυμαίνεται περίπου στη μέση τιμή λ με μία τυπική απόκλιση . Αυτές οι διακυμάνσεις σημειώνονται ως θόρυβος Poisson ή (ιδίως στην ηλεκτρονική) ως θόρυβος βολής.[εκκρεμεί παραπομπή]
Η συσχέτιση της μέσης τιμής και της τυπικής απόκλισης στη μέτρηση ανεξάρτητων διακριτών περιστατικών είναι χρήσιμη επιστημονικά. Παρακολουθώντας πως οι διακυμάνσεις ποικίλουν με το σήμα της μέσης τιμής, μπορεί κανείς να εκτιμήσει τη συμβολή μίας εμφάνισης, εάν ακόμα αυτή η συμβολή είναι πολύ μικρή για να ανιχνευθεί άμεσα . Για παράδειγμα, η φόρτιση e σε ένα ηλεκτρόνιο μπορεί να υπολογισθεί συσχετίζοντας το μέτρο ενός ηλεκτρικού ρέυματος με το θόρυβο βολής. Αν N ηλεκτρόνια περάσουν ένα σημείο σε μία δεδομένη στιγμή t κατά μέσο όρο, η μέση τιμή ρεύματος είναι ; καθώς οι διακυμάνσεις του ρεύματος θα πρέπει να είναι της τάξης του (δηλαδή, η τυπική απόκλιση της επεξεργασίας Poisson), η φόρτιση μπορεί να υπολογιστεί από το λόγο .[εκκρεμεί παραπομπή]
Ένα καθημερινό παράδειγμα είναι η κοκκοποίηση που εμφανίζεται καθώς μεγεθύνονται οι φωτογραφίες; η κοκκοποίηση είναι λόγω των διακυμάνσεων Poisson στον αριθμό των μειωμένων ασημένιων κόκκων, όχι των μεμονωμένων από μόνους τους κόκκων. Συσχετίζοντας την κοκκοποίηση με το βαθμό της διεύρυνσης , μπορεί κανείς να υπολογίσει τη συμβολή ενός μεμονωμένου κόκκου (η οποία είναι αλλιώς πολύ μικρή να τη δεις χωρίς βοήθεια).[εκκρεμεί παραπομπή] Πολλές άλλες μοριακές εφαρμογές του θορύβου Poisson έχουν αναπτυχθεί, π.χ., εκτίμηση του αριθμού πυκνότητας του υποδοχέα μορίων σε μία κυτταρική μεμβράνη.
Στη θεωρία αιτιωδών συνόλων τα διακεκριμένα στοιχεία του χωροχρόνου ακολουθούν μία κατανομή Poisson στον όγκο.
Παραγωγή τυχαίων μεταβλητών που ακολουθούν κατανομή Poisson[Επεξεργασία | επεξεργασία κώδικα]
Ένας απλός αλγόριθμος για να παραχθούν τυχαίοι αριθμοί που ακολουθούν κατανομή Poisson (ψευδο-τυχαία δειγματοληψία αριθμών) δόθηκε από τον Knuth (δες τις Παραπομπές πιο κάτω):
algorithm poisson random number (Knuth):
init:
Let L ← e−λ, k ← 0 and p ← 1.
do:
k ← k + 1.
Generate uniform random number u in [0,1] and let p ← p × u.
while p > L.
return k − 1.
Ενώ είναι απλός, η πολυπλοκότητα είναι γραμμική στην επιστρεφόμενη τιμή k, η οποία είναι λ κατά μέσο όρο. Υπάρχουν πολλοί άλλοι αλγόριθμοι για να ξεπεραστεί αυτό. Μερικοί δίνονται στο Ahrens & Dieter, δες Παραπομπές πιο κάτω. Επίσης, για μεγάλες τιμές του λ, μπορεί να υπάρχουν αριθμητικά προβλήματα σταθερότητας εξαιτίας του όρου e−λ. Μία λύση για τις μεγάλες τιμές του λ είναι η δειγματοληψία απόρριψης, ακόμα μία είναι να χρησιμοποιήσεις μία προσέγγιση Gaussian στην Poisson.
Ο αντίστροφος μετασχηματισμός δειγματοληψίας είναι απλός και αποδοτικός για μικρές τιμές του λ, και απαιτεί μόνον έναν ομοιόμορφο τυχαίο αριθμό u σε κάθε δείγμα. Οι αθροιστικές πιθανότητες εξετάζονται με τη σειρά μέχρι μία να ξεπεράσει το u.
Εκτίμηση παραμέτρου[Επεξεργασία | επεξεργασία κώδικα]
Μέγιστη πιθανότητα[Επεξεργασία | επεξεργασία κώδικα]
Δοθέντος ενός δείγματος n μετρήσιμων τιμών ki = 0,1,2,..., i = 1,...,n θέλουμε να εκτιμήσουμε την τιμή της παραμέτρου της κατανομής Πουασσόν με βάση την οποία πήραμε το δείγμα. Η μέγιστη πιθανότητα του εκτιμητή είναι:[31]
Δεδομένου οτι κάθε δείγμα έχει αναμενόμενη τιμή τότε αυτή είναι η μέση τιμή του δείγματος. Οπότε η μέγιστη πιθανότητα του εκτιμητή είναι ένας αμερόληπτος εκτιμητής του . Επίσης είναι ένας αποτελεσματικός εκτιμητής καθώς η διακύμανση του εκτιμητή πετυχαίνει το κατώτερο φράγμα Cramer-Rao (CRLB). Ως εκ τούτου είναι ένας αμερόλυπτος εκτιμητής με ελάχιστη διακύμανση. Επίσης μπορεί να αποδειχτεί ότι το άθροισμα (δηλαδή η μέση τιμή του δείγματος, αφού είναι ένα προς ένα συνάρτηση) είναι μια πλήρης και επαρκής στατιστική για το .
Για να αποδείξουμε την επάρκεια μπορούμε να χρησιμοποιήσουμε το θεώρημα παραγοντοποίησης. Σκεφτείτε να διαχωρίσεται το σώμα της συνάρτησης πιθανότητας της από κοινού κατανομής Poisson για το δείγμα σε δύο τμήματα:ένα το οποίο εξαρτάται αποκλειστικά από το δείγμα (Συμβολισμός ) και ένα που εξαρτάται από την παράμετρο και το δείγμα μόνο μέσω της συνάρτησης . Τότε η είναι επαρκής στατιστική για το .
Σημειώστε οτι ο πρώτος όρος εξαρτάται μόνο απο το . Ο δεύτερος όρος , εξαρτάται από το δείγμα μόνο μέσω της . Έτσι το είναι επαρκές.
Για λόγους πληρότητας μια οικογένεια κατανομών λέμε ό,τι έχει ολοκληρωθεί εάν και μόνο εάν συνεπάγοντας ό,τι για όλα τα . Εάν το μεμονομένο είναι ανεξάρτητες τότε, . Γνωρίζοντας την κατανομή που θέλουμε να ερευνήσουμε, είναι εύκολο να παρατηρήσουμε ότι το στατιστικό αποτέλεσμα έχει ολοκληρωθεί.
Για να ισχύει αυτή η ισότητα, είναι προφανές ότι το πρέπει να είναι 0. Αυτό προκύπτει από το γεγονός ότι κανένας απο τους άλλους όρους δεν θα είναι 0 για κάθε στο άθροισμα και για όλες τις πιθανές τιμές του .
Εξαιτίας αυτού, Η για όλα τα υπονοεί ότι , και το στατιστικό αποτέλεσμα έχει αποδειχθεί ότι έχει ολοκληρωθεί.
Όριο εμπιστοσύνης[Επεξεργασία | επεξεργασία κώδικα]
Το όριο εμπιστοσύνης για την μέση τιμή μιας κατανομής Πουασσόν μπορεί να εκφραστεί χρησιμοποιώντας την σχέση μεταξύ των αθροιστικών συναρτήσεων κατανομής Πουασσόν και της [[κατανομής x2]]. Η κατανομή x2 είναι από μόνη τους στενά συσχετιζόμενη με την κατανομή Γάμμα και αυτό οδηγεί σε μια εναλλακτική έκφραση. Δωθήσας μιας παρατήρησης και απο μια κατανομή Πουασσόν με μέση τιμή μ, ένα όριο εμπιστοσύνης για μ με επίπεδο εμπιστοσύνης είναι
ή ισοδύναμα,
όπου είναι η συνάρτηση quantile (που αντιστοιχεί σε μια χαμηλότερη περιοχή της ουράς p) της x2 κατανομής με n βαθμούς ελευθερίας και είναι η συνάρτηση quantile της γ κατανομή με παράμετρο σχήματος n και κλίμακα παραμέτρου 1.[20][32] Αυτό το διάστημα είναι "ακριβές" με την έννοια ότι η πιθανότητα κάλυψης δεν είναι ποτέ μικρότερη από το ονοματικό 1 – α.
Όταν quantile απο την γ κατανομή δεν είναι διαθέσιμα, μια ακριβής προσέγγιση σε αυτό το ακριβές διάστημα έχει προταθεί (βασισμένη στον Wilson–Hilferty μετασχηματισμό)[33]
όπου το υποδηλώνει την κανονική τυπική απόκλιση με ανώτερη περιοχή ουράς α / 2.
Για την εφαρμογή αυτών των τύπων στο ίδιο πλαίσιο όπως παραπάνω (δοθέντος ενός δείγματος διακριτών τιμών οι οποίες λαμβάνονται απο μια κανονική κατανομή με μέση τιμή ), κάποιος θα έθετε , υπολογίζοντας ένα διάστημα για , και μετά διαιρώντας το διάστημα με .
Μπεϋζιανή συμπερασματολογία[Επεξεργασία | επεξεργασία κώδικα]
Στην μπεϋζιανή συμπερασματολογία, η συζυγής πιθανότητα κατανομής για τον ρυθμό της παραμέτρου της κατανομής Πουασσόν είναι η Γάμμα κατανομή.[34] Έστω
σημειώνοντας ότι το είναι κατανεμημένο σύμφωνα με την συνάρτηση πυκνότητας πιθανότητας της γάμμα g παραμετροποιημένη με την έννοια μιας παραμέτρου σχήματος α και μιας αντίστροφης παραμέτρου κλίμακας β:
Τότε, δοθέντος ενός δείγματος n διακριτών τιμών ki όπως παραπάνω, και έχοντας απο πριν την Gamma(α, β), η παραπάνω κατανομή γίνεται:
Η μέση τιμή, E[], απο παραπάνω πλησιάζει την εκτίμηση της μέγιστης πιθανότητας όταν
Η οπίσθια προγνωστική κατανομή (posterior predictive distribution) σε ειδικές περιπτώσεις είναι αρνητική διωνυμική κατανομή,[35] η οποία μερικές φορές ονομάζεται Γάμμα - Πουασσόν κατανομή.
Ταυτόχρονη εκτίμηση των πολλαπλών μέσων τιμών Πουασσόν[Επεξεργασία | επεξεργασία κώδικα]
Έστω ότι είναι ένα σύνολο ανεξάρτητων μεταβλητών απο ένα σύνολο Πουασσόν κατανομών, καθένα με μια παράμετρο και θέλουμε να υπολογίσουμε αυτές τις παραμέτρους. Μετ'έπειτα, ο Clevenson και ο Zidek[36] έδειξαν ότι η κανονικοποιημένη απώλεια τετραγωνικού σφάλματος (normalized squared error loss) όταν , τότε, παρόμοια με το γνωστό παράδειγμα του Stein για τους κανονικούς μέσους, ο εκτιμητής MLE είναι απαράδεκτος.
Σε αυτή την περίπτωση, δίνεται μια οικογένεια minimax εκτημητών για κάθε και καθώς,[37]
Κατανομή Πουασσόν δυο μεταβλητών[Επεξεργασία | επεξεργασία κώδικα]
Η κατανομή αυτή έχει επεκταθεί στο διδιάστατο χώρο,[38]. Για παραμέτρους , η συνάρτηση μάζας πιθανότητας δίνεται από τον τυπο:
Οι περιθωριακές κατανομές της είναι και . Ο συντελεστής συσχέτισής της έχει εύρος
Ένας απλός τρόπος να παραχθεί μια κατανομή Πουασσόν δυο μεταβλητών, , είναι παίρνοντας τρία ανεξάρτητα δείγματα από κατανομές Πουασσόν , και . Έπειτα θέτουμε και . Η συνάρτηση πιθανότητας της κατανομής Πουασσόν δύο μεταβλητών είναι:
- .
Δείτε ακόμα[Επεξεργασία | επεξεργασία κώδικα]
- Σύνθετη κατανομή Πουασσόν
- Κατανομή Conway–Maxwell–Poisson (CMP ή COM-Poisson)
- Κατανομή Erlang
- Κατανομή Ερμίτ
- Δείκτης διασποράς
- Αρνητική διωνυμική κατανομή
- Συσσώρευση Πουασσόν
- Διαδικασία Πουασσόν
- Παλινδρόμηση Πουασσόν
- Δειγματοληψία Πουασσόν
- Θεωρία ουρών αναμονής
- Θεωρία ανανέωσης
- Το λήμμα του Robbins
- Κατανομή Tweedie
- Μοντέλο Μηδενικού-Φουσκόματος (Zero-inflated model)
- Μοντέλο Μηδενικά-περικομμένης κατανομής Πουασσόν (Zero-truncated Poisson distribution)
Υποσημειώσεις[Επεξεργασία | επεξεργασία κώδικα]
- ↑ Frank A. Haight (1967). Handbook of the Poisson Distribution. New York: John Wiley & Sons.
- ↑ 2,0 2,1 «Στατιστικές | Η κατανομή Poisson». Umass.edu. 24 Αυγούστου 2007. Αρχειοθετήθηκε από το πρωτότυπο στις 19 Απριλίου 2014. Ανακτήθηκε στις 18 Απριλίου 2014.
- ↑ S.D. Poisson, Probabilité des jugements en matière criminelle et en matière civile, précédées des règles générales du calcul des probabilitiés (Paris, France: Bachelier, 1837), σελίδα 206.
- ↑ 4,0 4,1 4,2 Johnson, N.L., Kotz, S., Kemp, A.W. (1993) Univariate Discrete distributions (2nd edition). Wiley. ISBN 0-471-54897-9, p157
- ↑ Ladislaus von Bortkiewicz, Das Gesetz der kleinen Zahlen [The law of small numbers] (Leipzig, Germany: B.G. Teubner, 1898). On σελίδα 1, Bortkiewicz presents the Poisson distribution. On σελίδες 23–25, Bortkiewicz presents his famous analysis of "4. Beispiel: Die durch Schlag eines Pferdes im preussischen Heere Getöteten." (4. Example: Those killed in the Prussian army by a horse's kick.).
- ↑ Probability and Stochastic Processes: A Friendly Introduction for Electrical and Computer Engineers, Roy D. Yates, David Goodman, page 60.
- ↑ For the proof, see : Απόδειξη βικι: μαθηματική ελπίδα and Απόδειξη βικι: διακύμανση
- ↑ Choi KP (1994) On the medians of Gamma distributions and an equation of Ramanujan. Proc Amer Math Soc 121 (1) 245–251
- ↑ Riordan, John (1937). «Moment recurrence relations for binomial, Poisson and hypergeometric frequency distributions». Annals of Mathematical Statistics 8: 103–111. doi:. https://archive.org/details/sim_annals-of-mathematical-statistics_1937-06_8_2/page/103. Also see Haight (1967), p. 6.
- ↑ E. L. Lehmann (1986). Testing Statistical Hypotheses (second έκδοση). New York: Springer Verlag. ISBN 0-387-94919-4. page 65.
- ↑ Raikov, D. (1937). On the decomposition of Poisson laws. Comptes Rendus (Doklady) de l' Academie des Sciences de l'URSS, 14, 9–11. (The proof is also given in von Mises, Richard (1964). Mathematical Theory of Probability and Statistics. New York: Academic Press.)
- ↑ Laha, R. G.· Rohatgi, V. K. (1979). Probability Theory. New York: John Wiley & Sons. σελ. 233. ISBN 0-471-03262-X.
- ↑ Johnson, N.L., Kotz, S., Kemp, A.W. (1993) Univariate Discrete distributions (2nd edition). Wiley. ISBN 0-471-54897-9, p159
- ↑ Michael Mitzenmacher and Eli Upfal (2005). Probability and Computing: Randomized Algorithms and Probabilistic Analysis. Cambridge University Press. σελ. 97. ISBN 0521835402.
- ↑ NIST/SEMATECH, '6.3.3.1. Counts Control Charts', e-Handbook of Statistical Methods, accessed 25 October 2006
- ↑ Huiming, Zhang; Lili Chu, Yu Diao (2012). «Some Properties of the Generalized Stuttering Poisson Distribution and its Applications». Studies in Mathematical Sciences 5 (1): 11–26. doi:. http://cscanada.net/index.php/sms/article/view/j.sms.1923845220120501.Z0697.
- ↑ McCullagh, Peter· Nelder, John (1989). Generalized Linear Models. London: Chapman and Hall. ISBN 0-412-31760-5. page 196 gives the approximation and higher order terms.
- ↑ 18,0 18,1 Johnson, N.L., Kotz, S., Kemp, A.W. (1993) Univariate Discrete distributions (2nd edition). Wiley. ISBN 0-471-54897-9, p163
- ↑ S. M. Ross (2007). Introduction to Probability Models (ninth έκδοση). Boston: Academic Press. ISBN 978-0-12-598062-3. pp. 307–308.
- ↑ 20,0 20,1 Johnson, N.L., Kotz, S., Kemp, A.W. (1993) Univariate Discrete distributions (2nd edition). Wiley. ISBN 0-471-54897-9, p171
- ↑ Johnson, N.L., Kotz, S., Kemp, A.W. (1993) Univariate Discrete distributions (2nd edition). Wiley. ISBN 0-471-54897-9, p153
- ↑ Xie, W.; Liao, H. (2013). "Some aspects in estimating warranty and post-warranty repair demands". Naval Research Logistics 60 (6): 499–511. doi:10.1002/nav.21548.
- ↑ Xie, W.; Liao, H.; Zhu, X. (2014). "Estimation of gross profit for a new durable product considering warranty and post-warranty repairs". IIE Transactions 46 (2): 87–105. doi:10.1080/0740817X.2012.761370.
- ↑ "The Poisson Process as a Model for a Diversity of Behavioural Phenomena"
- ↑ Philip J. Boland. «A Biographical Glimpse of William Sealy Gosset» (PDF). The American Statistician, Vol. 38, No. 3. (Aug., 1984), pp. 179–183. Αρχειοθετήθηκε από το πρωτότυπο (PDF) στις 29 Σεπτεμβρίου 2011. Ανακτήθηκε στις 22 Ιουνίου 2011.
- ↑
Aatish Bhatia. «What does randomness look like?».
Within a large area of London, the bombs weren’t being targeted. They rained down at random in a devastating, city-wide game of Russian roulette.
- ↑ P.X., Gallagher (1976). «On the distribution of primes in short intervals». Mathematika 23: 4–9. http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=7266644.
- ↑ A. Colin Cameron, Pravin K. Trivedi (1998). Regression Analysis of Count Data. Ανακτήθηκε στις 30 Ιανουαρίου 2013.
(p.5) The law of rare events states that the total number of events will follow, approximately, the Poisson distribution if an event may occur in any of a large number of trials but the probability of occurrence in any given trial is small.
- ↑ Edgeworth, F. Y. (1913). «On the use of the theory of probabilities in statistics relating to society». Journal of the Royal Statistical Society 76: 165–193. http://www.jstor.org/stable/10.2307/2340091.
- ↑ Good, I. J. (1986). «Some statistical applications of Poisson's work». Statistical Science 1 (2): 157–180. doi:. https://archive.org/details/sim_statistical-science_1986-05_1_2/page/157.
- ↑ Paszek, Ewa. «Maximum Likelihood Estimation – Examples».
- ↑ Garwood, F. (1936). "Fiducial Limits for the Poisson Distribution". Biometrika 28 (3/4): 437–442. doi:10.1093/biomet/28.3-4.437.
- ↑ Breslow, NE· Day, NE (1987). Statistical Methods in Cancer Research: Volume 2—The Design and Analysis of Cohort Studies. Paris: International Agency for Research on Cancer. ISBN 978-92-832-0182-3. Αρχειοθετήθηκε από το πρωτότυπο στις 8 Αυγούστου 2018. Ανακτήθηκε στις 30 Ιουνίου 2014.
- ↑ Fink, Daniel (1997) A Compendium of Conjugate Priors
- ↑ Gelman et al., Bayesian Data Analysis, 2nd ed. (2005) p. 60.
- ↑ Clevenson ML, Zidek JV (1975) Simultaneous Estimation of the Means of Independent Poisson Laws. Journal of the American Statistical Association 70(351a)
- ↑ Berger JO (1985) Statistical Decision Theory and Bayesian Analysis, 2nd Edition. Springer
- ↑ Loukas S, Kemp CD (1986) The index of dispersion test for the bivariate Poisson distribution. Biometrics 42(4) 941–948
Αναφορές[Επεξεργασία | επεξεργασία κώδικα]
- Joachim H. Ahrens, Ulrich Dieter (1974). «Computer Methods for Sampling from Gamma, Beta, Poisson and Binomial Distributions». Computing 12 (3): 223–246. doi:.
- Joachim H. Ahrens, Ulrich Dieter (1982). «Computer Generation of Poisson Deviates». ACM Transactions on Mathematical Software 8 (2): 163–179. doi:. https://archive.org/details/sim_acm-transactions-on-mathematical-software_1982-06_8_2/page/163.
- Ronald J. Evans, J. Boersma, N. M. Blachman, A. A. Jagers (1988). «The Entropy of a Poisson Distribution: Problem 87-6». SIAM Review 30 (2): 314–317. doi:.
- Donald E. Knuth (1969). Seminumerical Algorithms. The Art of Computer Programming, Volume 2. Addison Wesley.












![{\displaystyle \operatorname {E} [X^{(k)}]=\lambda ^{k}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d6f06c60618c08eb70f895c85d05327f99de70d5)





![{\displaystyle {\begin{aligned}\operatorname {E} [X]&=\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\cdot \lambda ^{x}}{x!}}\cdot x\\&=\lambda \cdot \sum _{x=1}^{\infty }{\frac {e^{-\lambda }\cdot \lambda ^{x-1}}{(x-1)!}}\\&=\lambda \cdot \sum _{x=0}^{\infty }{\frac {e^{-\lambda }\cdot \lambda ^{x}}{x!}}\\&=\lambda \cdot \sum _{x=0}^{\infty }\operatorname {P} (X=x)\\&=\lambda .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/743e0f96fefd24c3e61d700a822bf395bebc2722)
![{\displaystyle {\begin{aligned}\operatorname {E} [X\cdot (X-1)]&=\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\cdot \lambda ^{x}}{x!}}\cdot x\cdot (x-1)\\&=\lambda ^{2}\sum _{x=2}^{\infty }{\frac {e^{-\lambda }\cdot \lambda ^{x-2}}{(x-2)!}}\\&=\lambda ^{2}\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\cdot \lambda ^{x}}{x!}}\\&=\lambda ^{2}\sum _{x=0}^{\infty }\operatorname {P} (X=x)\\&=\lambda ^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97133ba9b48ef74c42344651b37aeeeefdd37860)
![{\displaystyle \operatorname {V} [X]=\operatorname {E} [X\cdot (X-1)]+\operatorname {E} [X]-(\operatorname {E} [X])^{2}=\lambda ^{2}+\lambda -\lambda ^{2}=\lambda .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02d7e1b11d635bde860c6344dd5504193493729c)
![{\displaystyle {\begin{aligned}\operatorname {E} [-\log _{2}X]&=-\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\cdot \lambda ^{x}}{x!}}\cdot \log _{2}\left({\frac {e^{-\lambda }\cdot \lambda ^{x}}{x!}}\right)\\&=-\log _{2}e^{-\lambda }\cdot \sum _{x=0}^{\infty }{\frac {e^{-\lambda }\cdot \lambda ^{x}}{x!}}-\log _{2}\lambda \cdot \sum _{x=0}^{\infty }{\frac {e^{-\lambda }\cdot \lambda ^{x}}{x!}}\cdot x-\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\cdot \lambda ^{x}}{x!}}\cdot \log _{2}x!\\&=-\log _{2}e^{-\lambda }\cdot \sum _{x=0}^{\infty }\operatorname {P} (X=x)-\log _{2}\lambda \cdot \sum _{x=0}^{\infty }\operatorname {E} [X]-e^{-\lambda }\cdot \sum _{x=0}^{\infty }{\frac {\lambda ^{x}}{x!}}\cdot \log _{2}x!\\&=\lambda \cdot (\log _{2}e-\log _{2}\lambda )+e^{-\lambda }\cdot \sum _{x=0}^{\infty }{\frac {\lambda ^{k}\log _{2}x!}{x!}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/30933f097cfc894057a1b547c914fdb4fea84ef8)



![{\displaystyle {\begin{aligned}\operatorname {E} [X^{(k)}]&=\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\lambda ^{x}}{x!}}\cdot x\cdot (x-1)\cdot \ldots \cdot (x-k+1)\\&=\lambda ^{k}\cdot \sum _{x=k}^{\infty }{\frac {e^{-\lambda }\lambda ^{x-k}}{(x-k)!}}\\&=\lambda ^{k}\cdot \sum _{x=0}^{\infty }{\frac {e^{-\lambda }\lambda ^{x}}{x!}}\\&=\lambda ^{k}\cdot \sum _{x=0}^{\infty }\operatorname {P} (X=x)\\&=\lambda ^{k}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59d45dc87ed135b22e374160c2a41e1eda0a9b0d)

![{\displaystyle {\begin{aligned}\operatorname {E} [t^{X}]&=\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\cdot \lambda ^{x}}{x!}}\cdot t^{x}\\&=\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\cdot (\lambda \cdot t)^{x}}{x!}}\\&=e^{-\lambda +\lambda \cdot e^{t}}\cdot \sum _{x=0}^{\infty }{\frac {e^{-\lambda \cdot t}\cdot (\lambda \cdot t)^{x}}{x!}}\\&=e^{-\lambda +\lambda \cdot t}\cdot \sum _{y=0}^{\infty }\operatorname {P} (X=y)\\&=e^{-\lambda +\lambda \cdot t}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5d7d75765902cd907f9ca33e00011c482f7bc5c)

![{\displaystyle {\begin{aligned}\operatorname {E} [e^{tX}]&=\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\cdot \lambda ^{x}}{x!}}\cdot e^{tx}\\&=\sum _{x=0}^{\infty }{\frac {e^{-\lambda }\cdot (\lambda \cdot e^{t})^{x}}{x!}}\\&=e^{-\lambda +\lambda \cdot e^{t}}\cdot \sum _{x=0}^{\infty }{\frac {e^{-\lambda \cdot e^{t}}\cdot (\lambda \cdot e^{t})^{x}}{x!}}\\&=e^{-\lambda +\lambda \cdot e^{t}}\cdot \sum _{y=0}^{\infty }\operatorname {P} (X=y)\\&=e^{-\lambda +\lambda \cdot e^{t}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c91b906d5e8d0184049bf2aa77d3f8ee2659dc3e)









































































































![{\displaystyle g(u,v)=\exp[(\theta _{1}-\theta _{12})(u-1)+(\theta _{2}-\theta _{12})(v-1)+\theta _{12}(uv-1)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c0bfa594688065653a236accbe2ca3e0f5d3ee9f)









