Θεωρία χορδών
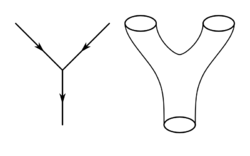
Οι Θεωρίες Χορδών είναι μοντέλα της φυσικής στα οποία τα θεμελιώδη δομικά στοιχεία είναι μονοδιάστατα εκτεταμένα αντικείμενα (Χορδές), σε αντίθεση με την παραδοσιακή έννοια των σημειακών και αδιάστατων στοιχειωδών σωματιδίων. Οι θεωρίες χορδών αποφεύγουν με αυτό τον τρόπο τα προβλήματα και τις ανωμαλίες που προκύπτουν στις φυσικές θεωρίες λόγω της σημειακής φύσης των σωματιδίων. Στη μελέτη των θεωριών χορδών περιλαμβάνονται όχι μόνο μονοδιάστατα αντικείμενα, αλλά και αντικείμενα περισσότερων διαστάσεων, που καλούνται βράνες. Μέχρι σήμερα δεν έχει υπάρξει πειραματική επαλήθευση της θεωρίας χορδών.
Γενική περιγραφή[Επεξεργασία | επεξεργασία κώδικα]

Η έρευνα γύρω από τη θεωρία χορδών αποσκοπεί στην εξαγωγή μιας θεωρίας των πάντων. Είναι προς το παρόν η μόνη αξιόπιστη θεωρία κβαντικής βαρύτητας, η οποία μπορεί εξίσου καλά να περιγράψει και τις ηλεκτρομαγνητικές και τις άλλες θεμελιώδεις αλληλεπιδράσεις. Στη θεωρία υπερχορδών περιλαμβάνονται και τα φερμιόνια, οι θεμελιώδεις δομικοί λίθοι της ύλης. Δεν είναι, πάντως, ακόμη γνωστό αν η θεωρία υπερχορδών είναι η ακριβής θεωρία του σύμπαντος, ούτε τα περιθώρια των τιμών των φυσικών σταθερών που προβλέπει.
Το γεγονός ότι ο κόσμος είναι τρισδιάστατος έρχεται εκ πρώτης όψεος σε αντίθεση με τις 10 διαστάσεις της θεωρίας. Οι πιθανές απαντήσεις σ'αυτό το παράδοξο είναι δύο: Μία πιθανή απάντηση είναι ότι οι υπόλοιπες 7 διαστάσεις είναι τόσο μικρές ώστε δεν είναι δυνατό να παρατηρηθούν. Στην 6-διάστατη περίπτωση αναφέρονται οι υπερχώροι Καλάμπι-Γιάου. Στις 7 διαστάσεις αναφέρονται οι χώροι πολλαπλότητας G2. Η δεύτερη πιθανή απάντηση λύση είναι ότι είμαστε δεσμευμένοι σε μία υπερ-μεμβράνη του πλήρους σύμπαντος τεσσάρων χωροχρονικών διαστάσεων. Η λύση αυτή είναι γνωστή ως brane-world theory. [1][2] Ορισμένες εκδοχές αυτής της θεωρίας οδηγούν σε προβλέψεις που θα μπορέσουν να ελεγχθούν από πειραματικές μετρήσεις κβαντικής βαρύτητας που θα γίνουν στον επιταχυντή LHC του διεθνούς ερευνητικού κέντρου CERN της Γενεύης, ο οποίος έχει ήδη αρχίσει τη λειτουργία του.
Θεωρίες και δυϊσμοί[Επεξεργασία | επεξεργασία κώδικα]
Υπάρχουν 2 κύριες θεωρίες χορδών, η μποζονική θεωρία χορδών σε 26 διαστάσεις και η Υπερσυμμετρική Θεωρία Χορδών σε 10 διαστάσεις. Σήμερα, ο όρος θεωρία χορδών αναφέρεται στην Υπερσυμμετρική θεωρία χορδών ή Θεωρία Υπερχορδών. Μια σημαντική ερευνητική ανακάλυψη που έγινε στη δεκαετία του 1990 ήταν το ότι οι διάφορες θεωρίες υπερχορδών μπορούν να προκύψουν σαν οριακές περιπτώσεις από μια σχετικά άγνωστη 11-διάστατη θεωρία που ονομάστηκε Θεωρία-Μ (M-Theory).[3]
| Θεωρίες Χορδών | ||
|---|---|---|
| Τύπος | Χωροχρονικές διαστάσεις |
Λεπτομέρειες |
| Μποζονική | 26 | Μόνο μποζόνια, όχι φερμιόνια, όχι ύλη, με ανοικτές και κλειστές χορδές. Βασικό μειονέκτημα: ένα σωματίδιο με φανταστική μάζα, που ονομάζεται ταχυόνιο. |
| I | 10 | Υπερσυμμετρία μεταξύ των δυνάμεων και της ύλης, με ανοικτές και κλειστές χορδές, όχι ταχυόνια, η ομάδα συμμετρίας είναι η SO(32). |
| IIA | 10 | Υπερσυμμετρία μεταξύ των δυνάμεων και της ύλης, με ανοικτές και κλειστές χορδές, όχι ταχυόνια, άμαζα φερμιόνια με διπλή ελικότητα (nonchiral). |
| IIB | 10 | Υπερσυμμετρία μεταξύ των δυνάμεων και της ύλης, με ανοικτές και κλειστές χορδές, όχι ταχυόνια, άμαζα φερμιόνια με μονή ελικότητα (chiral). |
| HO | 10 | Υπερσυμμετρία μεταξύ των δυνάμεων και της ύλης, με ανοικτές και κλειστές χορδές, όχι ταχυόνια, ετεροτική, που σημαίνει ότι οι χορδές που κινούνται δεξιόστροφα διαφέρουν με αυτές που κινούνται αριστερόστροφα, η ομάδα συμμετρίας είναι η SO(32). |
| HE | 10 | Υπερσυμμετρία μεταξύ των δυνάμεων και της ύλης, με ανοικτές και κλειστές χορδές, όχι ταχυόνια, ετεροτική, που σημαίνει ότι οι χορδές που κινούνται δεξιόστροφα διαφέρουν με αυτές που κινούνται αριστερόστροφα, η ομάδα συμμετρίας είναι η E8×E8. |
Πριν τη δεκαετία του '90, οι πέντε διαφορετικοί τύποι θεωριών χορδών έμοιαζαν ασύνδετες μεταξύ τους. Στο ετήσιο συνέδριο των φυσικών πάνω στη θεωρία χορδών που πραγματοποιήθηκε το 1995, ο Έντουαρντ Βίτεν πρότεινε πως οι διαφορετικοί αυτοί τύποι μπορούν ίσως να προκύψουν ως οριακές περιπτώσεις μιας άγνωστης ακόμη 11-διάστατης θεωρίας που ονομάστηκε θεωρία-Μ.
Ανακαλύφθηκαν επίσης κάποιες σχέσεις που ονομάζονται δυϊσμοί (dualities), και οι οποίες δείχνουν ότι οι 5 διαφορετικές θεωρίες χορδών συνδέονται άμεσα μεταξύ τους, σε χαμηλά ή υψηλά όρια διαφόρων σταθερών, δίνοντας έτσι τα ίδια ακριβώς αποτελέσματα. Οι δυϊσμοί αυτοί είναι ο S-δυϊσμός, ο Τ-δυϊσμός και ο U-δυϊσμός.
Προβλήματα της θεωρίας χορδών[Επεξεργασία | επεξεργασία κώδικα]
Η θεωρία χορδών δεν έχει μέχρι στιγμής επιτύχει να κάνει ποσοτικές προβλέψεις που θα μπορούσαν να επαληθευθούν πειραματικά. Επικριτές της θεωρίας υποστηρίζουν μάλιστα ότι η θεωρία δεν είναι δυνατό ούτε να επαληθευτεί ούτε να απορριφθεί. Οι υποστηρικτές της αντιλέγουν ότι η θεωρία χορδών έχει ήδη κάνει πληθώρα νέων προβλέψεων: α) Έξτρα διαστάσεις. Η πρόβλεψη αυτή αποτελεί αντικείμενο πολλών εξελισσόμενων πειραμάτων παγκοσμίως. β) Νέα σωματίδια με μάζες συγκρίσιμες της μάζας του Planck. γ) Υπερσυμμετρία-υπερβαρύτητα. Η ύπαρξη ή όχι υπερσυμμετρικών σωματιδίων θα αποτελέσει το αντικείμενο σειράς πειραμάτων που αναμένεται να αρχίσουν σύντομα[ασαφές] στον επιταχυντή LHC του CERN.
Η διατύπωση της θεωρίας υπερχορδών έχει γίνει με βάση σειράς διαταραχών, και όχι ως ακριβώς διατυπωμένη θεωρία. Παρόλο που υπάρχει αρκετή πρόοδος προς μια μη-διαταρακτική διατύπωση, και υποθέσεις για πλήρεις ορισμούς στο χωροχρόνο που ικανοποιούν ορισμένες ασύμπτωτες, δεν έχει διατυπωθεί ακόμη μια πλήρης μη-διαταρακτική θεωρία υπερχορδών.
Επιτυχίες της θεωρίας υπερχορδών[Επεξεργασία | επεξεργασία κώδικα]
- Σημαντικότατες συνεισφορές σε διάφορους κλάδους των μαθηματικών.
- Συμμετρία κατόπτρου (mirror symmetry).
- Σημαντικές ανακαλύψεις στην Θεωρία κόμβων (knot theory).
- Μελέτη των χώρων Calabi-Yau.
- Πρόσφατες συνεισφορές στο πρόγραμμα Langlands. [4]
- Μικροσκοπική απόδειξη της εξίσωσης Bekenstein-Hawking για την εντροπία των μελανών οπών.[5]
- Σημαντική πρόοδο στην κατανόηση ορισμένων ισχυρά συζευγμένων θεωριών πεδίου, μέσω του δυϊσμού σύμμορφης θεωρίας πεδίου--βαρύτητας AdS.[6]
- Σημαντική πρόοδο στη μελέτη των υπερσυμμετρικών θεωριών βαθμίδας, στις οποίες περιλαμβάνονται και πιθανές επεκτάσεις του Τυποποιημένου Μοντέλου.
Σχετικά θέματα[Επεξεργασία | επεξεργασία κώδικα]
- Centauro γεγονότα
- Θεωρία Υπερχορδών
- Θεωρία-Μ
- Κβαντική Βαρύτητα
- Θεωρία Kaluza-Klein
- Υπερσυμμετρία, Υπερβαρύτητα
Παραπομπές[Επεξεργασία | επεξεργασία κώδικα]
- ↑ L. Randall and R. Sundrum, "An alternative to compactification", Phys. Rev. Lett. 83 (1999) 4690, hep-th/9906064.
- ↑ L. Randall and R. Sundrum, "A large mass hierarchy from a small extra dimension", Phys. Rev. Lett. 83 (1999) 3370, hep-ph/9905221.
- ↑ E. Witten, "String theory dynamics in various dimensions", Nucl. Phys. B 443 (1995) 85, hep-th/9503124].
- ↑ A. Kapustin and E. Witten, "Electric-magnetic duality and the geometric Langlands program", hep-th/0604151.
- ↑ A. Strominger and C. Vafa, "Microscopic Origin of the Bekenstein-Hawking Entropy", Phys. Lett. B 379 (1996) 99, hep-th/9601029.
- ↑ J. M. Maldacena, "The large N limit of superconformal field theories and supergravity", Adv. Theor. Math. Phys. 2 (1998) 231; Int. J. Theor. Phys. 38 (1999) 1113, hep-th/9711200.
Εξωτερικοί σύνδεσμοι[Επεξεργασία | επεξεργασία κώδικα]
- Brian Greene documentary (Αγγλικά).
- The Elegant Universe online (Αγγλικά).
- Η επίσημη σελίδα της θεωρίας υπερχορδών (Αγγλικά).
|
