Απόσταση Hamming

Δυαδικός κύβος 3-bit για την εύρεση της απόστασης Hamming

Δύο παραδείγματα αποστάσεων: 100->011 έχει απόσταση (κόκκινο μονοπάτι), 010->111 έχει απόσταση 2 (μπλε μονοπάτι)

Δυαδικός υπερκύβος 4-bit για την εύρεση της απόστασης Hamming

Δύο παραδείγματα αποστάσεων: 0100->1001 έχει απόσταση (κόκκινο μονοπάτι), 0110->1110έχει απόσταση 1 (μπλε μονοπάτι)

Στην θεωρία πληροφορίας, ως απόσταση Hamming μεταξύ δύο συμβολοσειρών ίσου μήκους ορίζεται ο αριθμός θέσεων στις οποίες τα αντίστοιχα σύμβολα είναι διαφορετικά. Η απόσταση Hamming, μετρά τον ελάχιστο αριθμό αντικαταστάσεων που χρειάζονται ώστε να μετατραπεί η μία συμβολοσειρά στην άλλη, ή αλλιώς, τον αριθμό των λαθών που μετέτρεψαν την μία συμβολοσειρά στην άλλη.

Παραδείγματα

Η απόσταση Hamming μεταξύ:

• "τόνος" και "πόθοι" είναι 3.
• 1011101 και 1001001 είναι 2.
• 2173896 και 2233796 είναι 3.

Ειδικές ιδιότητες

Για δεδομένο μήκος n, η απόσταση Hamming είναι μετρική στον διανυσματικό χώρο των λέξεων αυτού του μήκους, καθώς εμφανώς ικανοποιεί τις προϋποθέσεις της μη αρνητικότητας, της ταυτότητας των μη διακρισίμων και της συμμετρίας, και μπορεί να δειχθεί εύκολα με πλήρη επαγωγή ότι ικανοποιεί και την τριγωνική ανισότητα. Η απόσταση Hamming μεταξύ δύο λέξεων a και b μπορεί επίσης να ειδωθεί ως το βάρος Hamming του a−b για κατάλληλη του τελεστή −.

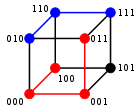
Για δυαδικές συμβολοσειρές a και b η απόσταση Hamming είναι ίση με τον αριθμό των μονάδων στο a XOR b. Ο μετρικός χώρος δυαδικών συμβολοσειρών μήκους n, με την απόσταση Hamming είναι γνωστός ως κύβος Hamming. Είναι ισοδύναμος ως μετρικός χώρος με το σύνολο των αποστάσεων μεταξύ κορυφών σε ένα γράφημα υπερκύβου. Αν η δυαδική συμβολοσειρά μήκους n θεωρηθεί ως διάνυσμα στο $R^n$ μεταχειρίζοντας κάθε σύμβολο της ως πραγματική συντεταγμένη, οι συμβολοσειρές σχηματίζουν τις κορυφές ενός n-διάστατου υπερκύβου, και η απόσταση Hamming των συμβολοσειρών είναι ισοδύναμη με την απόσταση Manhattan των κορυφών.

Ιστορία και εφαρμογές

Η απόσταση Hamming πήρε το όνομά της από τον Ρίτσαρντ Χάμινγκ (Richard Hamming), ο οποίος την εισήγαγε στην θεμελιώδη εργασία του για τους κώδικες Hamming, Error detecting and error correcting codes (Κώδικες εντοπισμού και διόρθωσης σφαλμάτων, 1950). Χρησιμοποιείται στην τηλεπικοινωνία για την μέτρηση των ανεστραμμένων bit σε μία σταθερού μήκους ψηφιακή λέξη ως εκτίμηση σφάλματος, και συνεπώς μερικές φορές αποκαλείται και απόσταση σήματος. Η ανάλυση βάρους Hamming χρησιμοποιείται σε αρκετούς τομείς, όπως η θεωρία πληροφορίας, θεωρία κωδικοποίησης και κρυπτογραφία. Ωστόσο για την σύγκριση συμβολοσειρών διαφορετικού μήκους, ή συμβολοσειρών όπου δεν έχουν γίνει μόνο αντικαταστάσεις αλλά αναμένονται και εισαγωγές ή διαγραφές είναι καταλληλότερες πιο πολύπλοκες μέθοδοι όπως η απόσταση Levenshtein. Για q-δικές συμβολοσειρές επί ενός αλφάβητου μεγέθους q ≥ 2 η απόσταση Hamming εφαρμόζεται στην περίπτωση της ορθογωνικής διαμόρφωσης, ενώ η απόσταση Lee χρησιμοποιείται για την φασική διαμόρφωση. Αν q = 2 ή q = 3 οι αποστάσεις συμπίπτουν.

Η απόσταση Hamming χρησιμοποιείται επίσης στη συστηματική ως μέτρο της γενετικής απόστασης.

Πηγές

• Hamming, Richard W. (1950), "Error detecting and error correcting codes", Bell System Technical Journal 29 (2): 147–160, MR0035935, http://www.caip.rutgers.edu/~bushnell/dsdwebsite/hamming.pdf .
• Pilcher, C. D.; Wong, J. K.; Pillai, S. K. (March 2008), "Inferring HIV transmission dynamics from phylogenetic sequence relationships", PLoS Med. 5 (3): e69, doi:10.1371/journal.pmed.0050069, PMID 18351799 .
• Wegner, Peter (1960), "A technique for counting ones in a binary computer", Communications of the ACM 3 (5): 322, doi:10.1145/367236.367286 .